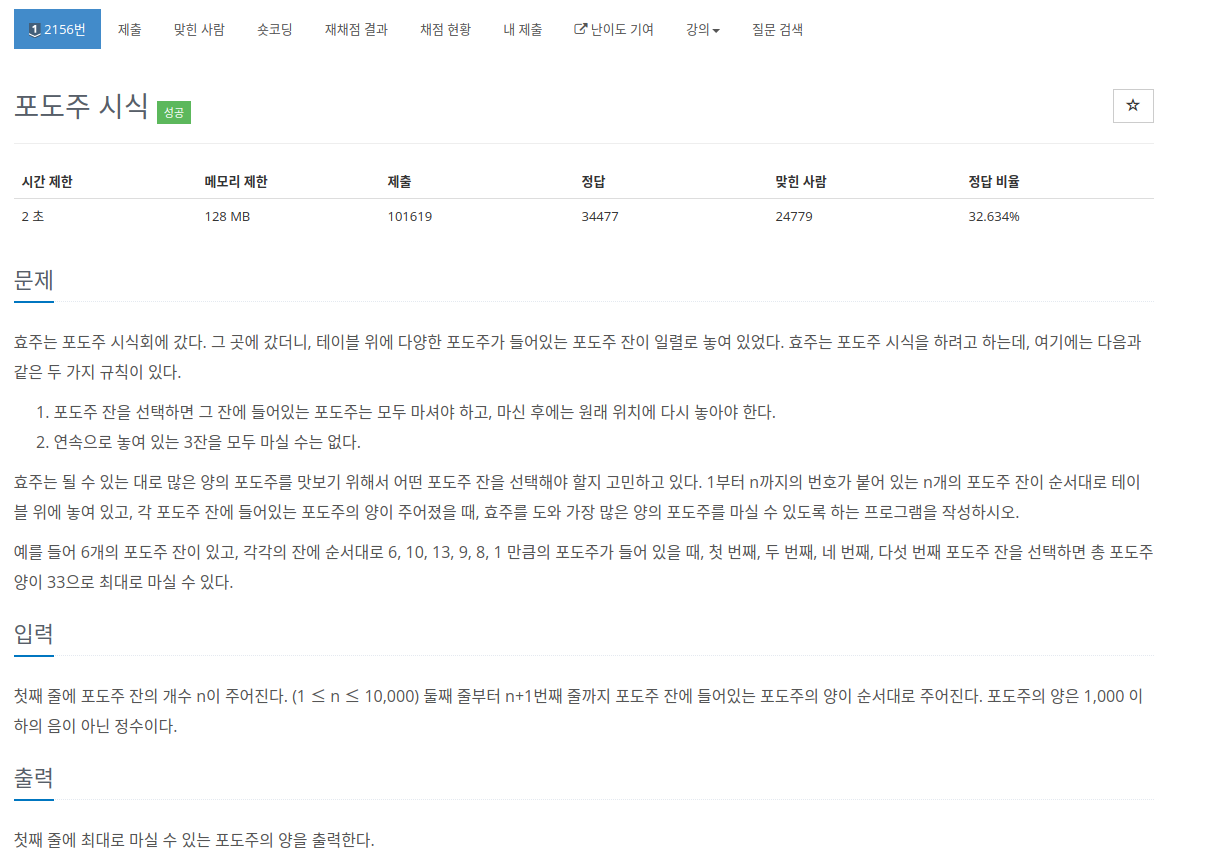
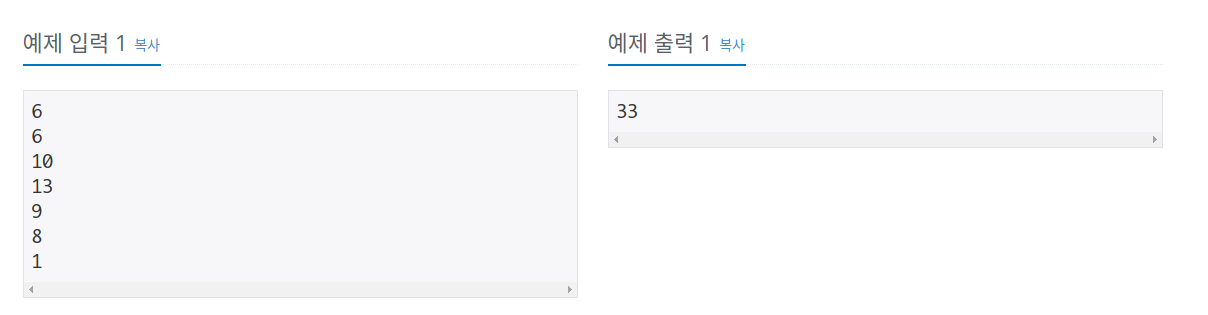
문제

풀이

이문제도 정말 삽질 많이했다.
결론만 하자면 정말 간단하다.
결국 이 주어진 규칙에서
dp[i]는 i번째를 마셨을 때 A와 안마셨을때 B로나누고
A일때는
1. i-1을 마셨을때와
2. i-1을 안마셨을 때로 나눌수있다.

또한 테이블 dp[i]가 나타내는 것은 i까지의 포도주중 마실 수 있는 포도주의 양의 최댓값이며,

A일때 점화식은
dp[i] = glass[i] + max(1.일때, 2일때)로 볼 수 있고

1.일때를 점화식을 세워보면
i-1번째와 i번째를 마셨으므로 최소 i-3번째 부터 마실 수 있고

2.일때 점화식을 세워보면
i번째를 마시고 i-1번째를 안마시므로 최소 i-2번째 부터 마실 수 있다.

따라서 A일때 점화식은
dp[i] = glass[i] + max(dp[i-3] + glass[i-1], dp[i-2])로 볼 수 있다.

B일때 점화식은
dp[i] = dp[i-1]로 볼 수 있고

따라서 이 내용들을 코드로 구현하면

코드

#입력
# 첫째 줄에 포도주 잔의 개수 n이 주어진다. (1 ≤ n ≤ 10,000) 둘째 줄부터 n+1번째 줄까지 포도주 잔에 들어있는 포도주의 양이 순서대로 주어진다. 포도주의 양은 1,000 이하의 음이 아닌 정수이다.

#점화식
#dp[i] = max(dp[i-2] + glass[i], dp[i-3] + glass[i-1] + glass[i])


import sys

n = int(input())

glass = list()
glass.append(0)
for i in range(n):
  glass.append(int(sys.stdin.readline().rstrip()))

dp = [0] * (n+1)
dp[1] = glass[1]

if(n > 1):
  dp[2] = glass[1] + glass[2]

for i in range(3, n+1):
  dp[i] = glass[i] + max(dp[i-3] + glass[i-1], dp[i-2])
  dp[i] = max(dp[i], dp[i-1])

print(dp[n])