Abstract
BERT와 같은 Transformer 기반의 모델들은 NLP에서 매우 성공적인 deep learning model이 되었음.
하지만, full attention mechanism을 수행으로 인한 sequence 길이에 따른 quadratic dependency가 주요 한계임.
Big Bird는 sparse attention mechanism을 사용하여 quadratic dependency를 선형으로 줄일 수 있음.
sparse attention으로 인해 비슷한 하드웨어를 사용하고도 8배의 길이의 sequence를 다룰 수 있게 됨.
이로 인해, QA나 summarization 같은 다양한 NLP task에 성능을 향상시켰음.
Introduction
Transformer는 self-attention mechanism으로 input sequence의 각 토큰을 병렬로 처리할 수 있고, RNN의 sequential dependency도 해결할 수 있었음. (모든 토큰에 대해 독립적으로 attention 가능)
self-attention은 계산과 메모리 요구가 sequence 길이의 제곱에 비례하게 증가함.
대략 512 토큰 길이의 input sequence를 다룰 수 있는데 이는 QA나 document classification과 같이 큰 context에서 적용하기 어려움.
📍 2가지의 아이디어를 바탕으로 연구를 진행함.
① 더 적은 inner-product를 사용하여 fully quadratic self-attention의 이점을 달성할 수 있을까?
② sparse attention mechanism으로 원래 네트워크의 expressivity와 flexibility를 보존할 수 있을까?
Big Bird는 3가지 main part로 이루어짐.
✅ sequence의 모든 부분에 attention하는 g개의 global token
✅ 모든 토큰이 w개의 local neighboring token에 attention함.
✅ 모든 토큰이 r개의 random token에 attention함.
→ 더 긴 sequence 길이(8배)에 높은 성능의 attention mechanism을 수행할 수 있음.
Related Work
두 가지의 방법으로 Transformer의 quadratic dependency를 해결하고자 했음.
- 길이 제한을 받아들이고(입력 문장의 길이 : 512 token) 발전시키기 (ex. sliding window)
SpanBERT, ORQA, REALM, RAG - 입력 문장의 길이를 늘리기 위해 full attention을 하지 않는 approach
Reformer, BlockBERT, Longformer
→ Big Bird도 여기에 해당❗
BigBird Architecture
Bir Bird는 multi-head attention과 feed forward network로 이루어진 layer를 쌓아서 만든 Transformer 구조 기반임.
✔ self-attention layer에서 full-attention 이 아닌 generalised attention mechanism을 사용함.
generalised attention mechanism은 노드(vertex) 집합 이고, inner product의 집합인 attention mechanism을 수행하는 directed edge로 이루어진 directed graph D로 나타낼 수 있음.
input 차원으로 embedding된 input sequence x
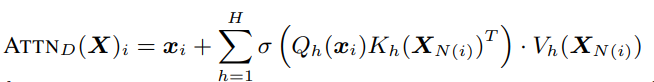

n×n이고 query i가 key j에 attention하는 경우 이고 그렇지 않은 경우
예를 들어, full self attention(모든 token이 다른 모든 token을 attention)을 하는 BERT같은 경우, matrix가 모두 1이 되며 quadratic complexity를 유발함.
→ self-attention의 fully connected graph의 관점을 통해 complexity를 줄이기 위해 기존의 graph theory를 사용할 수 있음.
📌 graph sparsification problem : self-attention의 quadratic complexity를 줄이기 위한 문제
📍 attention mechanism을 위한 sparse random graph에서 필요한 2가지
1. small average path length between nodes
간단한 random graph 구조인 Erdos-Rényi model를 보면, 각 edge는 고정된 확률로 독립적이게 선택됨. 두 노드간의 가장 짧은 길이는 logarithmic에 비례함. random graph는 complete graph의 spectral property를 근사하고, (인접 행렬의) 두 번째 고유값은 첫 번째 교유값과 멀어지게 됨.
→ 그래프 내에 mixing time for random walks가 빠르기 때문에 임의의 두 노드 사이를 빠르게 흐를 수 있음.
본 연구에서는 각 query가 r개의 random key를 attention하는 sparse attention을 제안함.
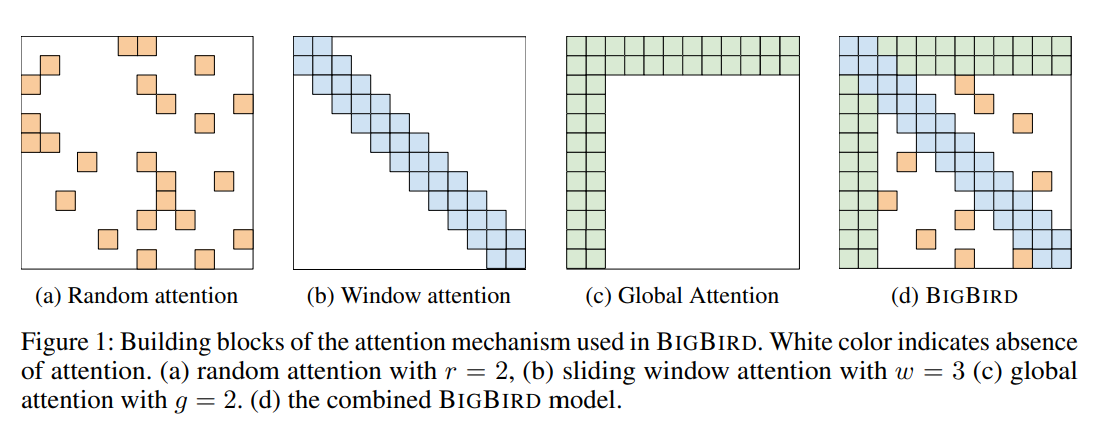
A(i, ·) = 1로 random하게 선택된 r개의 키, Figure1-(a)
2. notion of locality
locality of reference → 토큰에 대한 많은 정보는 주변 토큰으로부터 유도됨.
그래프 이론에 적용하면, clustering coefficient는 connectivity의 locality를 측정하는 지표이고 그래프가 많은 clique, 가까운 clique를 포함하면 clustering coefficient가 높아짐.
노드에 대한 sliding window로 시작 → 모든 연결의 랜덤한 부분집합(k%)은 랜덤한 연결로 교체, (100-k)% 연결은 유지
window size가 w인 self attention 중에 위치 i의 쿼리가 i-w/2에서 i+w/2까지의 key에 attention함.
A(i, i-w/2 : i+w/2) = 1 (Figure1-(b))
✔ random block과 local window로 필요한 모든 context를 포착하는 것은 BERT의 성능보다 부족했음.
이론적 분석과 경험적 성능에 거쳐서 "global tokens"(토큰이 시퀀스에 있는 모든 토큰들에 attention)의 중요성을 활용함. Figure1-(c)
📍 global token은 2가지로 정의됨.
- BigBird-ITC(Internal Transformer Construction) : 기존의 일부 토큰들을 전체 sequence에 attention하도록 "global"하게 만들어줌. A(i, :) = 1 및 A(:, i) = 1이 되도록 인덱스의 부분집합 G를 선택 (i ∈ G)
- BigBird-ETC(Extended Transformer Construction) : CLS와 같은 추가 "global" token 포함. 모든 기존 토큰에 attention하는 g개의 global token 추가.
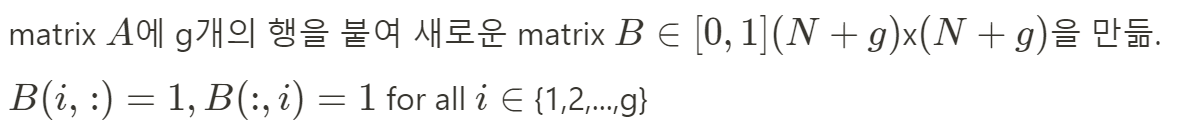
→ context를 추가할 추가적인 공간을 더할 수 있고 성능이 향상된 것을 볼 수 있음.
✔ 최종적으로 사용하는 attention mechanism = random attention + window attention + global attention Figure1-(d)
random attention query가 r개의 random한 key에 attention
window attention 각 query는 왼쪽, 오른쪽에 w/2개의 token에 attention
global attention g개의 global token 포함 (global token은 기존 token이거나 추가된 token임.)
📌 Implementation details
GPU 및 TPU와 같은 하드웨어 가속기는 연속된 바이트 블록을 한 번에 load하는 병합된 메모리 작업에서 효과적으로 작동함. → sliding window or random element queries로 인한 small sporadic look-ups는 효율적X
→ "blockifying"로 완화
query, key 벡터가 각각 12개씩 있는 경우, block size를 2로 설정하여 query matrix를 12/2 = 6개 block으로 나누고 key matrix도 12/2 = 6개 block으로 나눔. (query block과 key block의 수는 동일해야 함)
1. Random attention : 각 query block은 r개의 random key block에 attention함.
Figure 3(a)r = 1이고 block size=2 → 크기 2의 각 query block이 크기 2의 random key block에 random attention함.
2. Window local attention : block을 만들면서 #query_block = #key_block이도록 함. → block window attention 정의하는데 도움을 줌. 각 query block j는 index j - (w - 1)/2에서 j + (w - 1)/2까지의 key block에 attention함.
Figure 3(b)w=3, block size=2 → 각 query block j (크기 2의 query)이 key block j - 1, j, j + 1에 attention함.
3. Global attention : Global block과 모든 block들과의 attention 계산 (block 단위로 계산)
Figure 3(c)g = 1, block size=2 / BIGBIRD-ITC의 경우 한 query block과 key block이 모든 block에 attention함.
Theoretical Results about Sparse Attention Mechanism
sparse attention이 2가지 측면에서 full-attention mechanism과 마찬가지로 강력함.
① sparse attention mechanism이 독립적인 encoder에서 사용될 때, seq2seq 함수의 Universal Approximator임.
② sparse encoder-decoder trasformer는 Turing Complete임.
Experiments : Natural Language Processing
MLM을 시작으로, 더 긴 연속적인 sequence를 활용하여 더 나은 contextual representation을 학습할 수 있는지 확인하고 QA와 document classification task에 적용함.
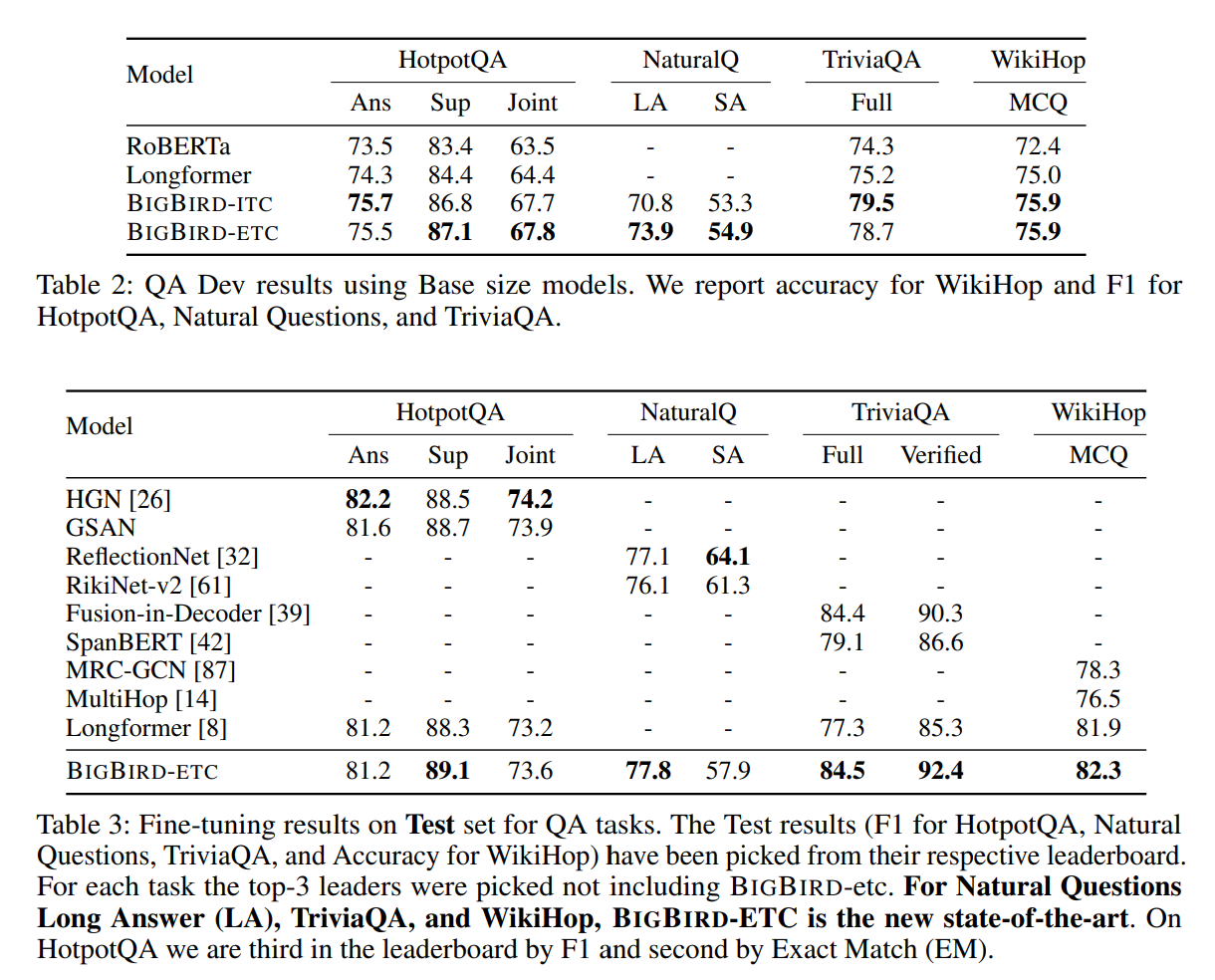
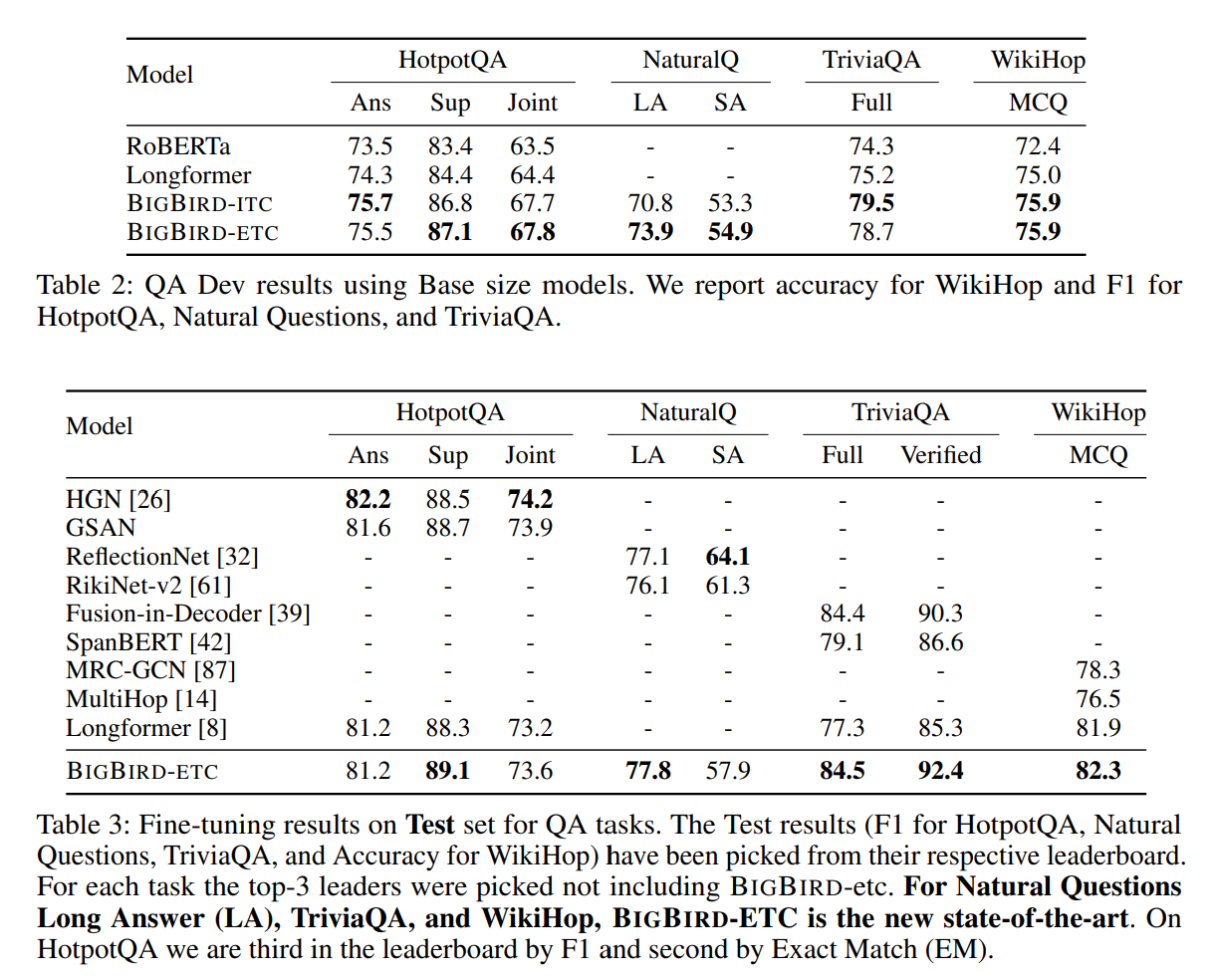
Encoder-Decoder Tasks
Big Bird의 encoder 부분에만 sparse attention mechanism 사용 / decoder에는 full attention 사용
→ 실제 generative application에서 input에 비해 ouput sequence의 길이가 대체적으로 작기 때문
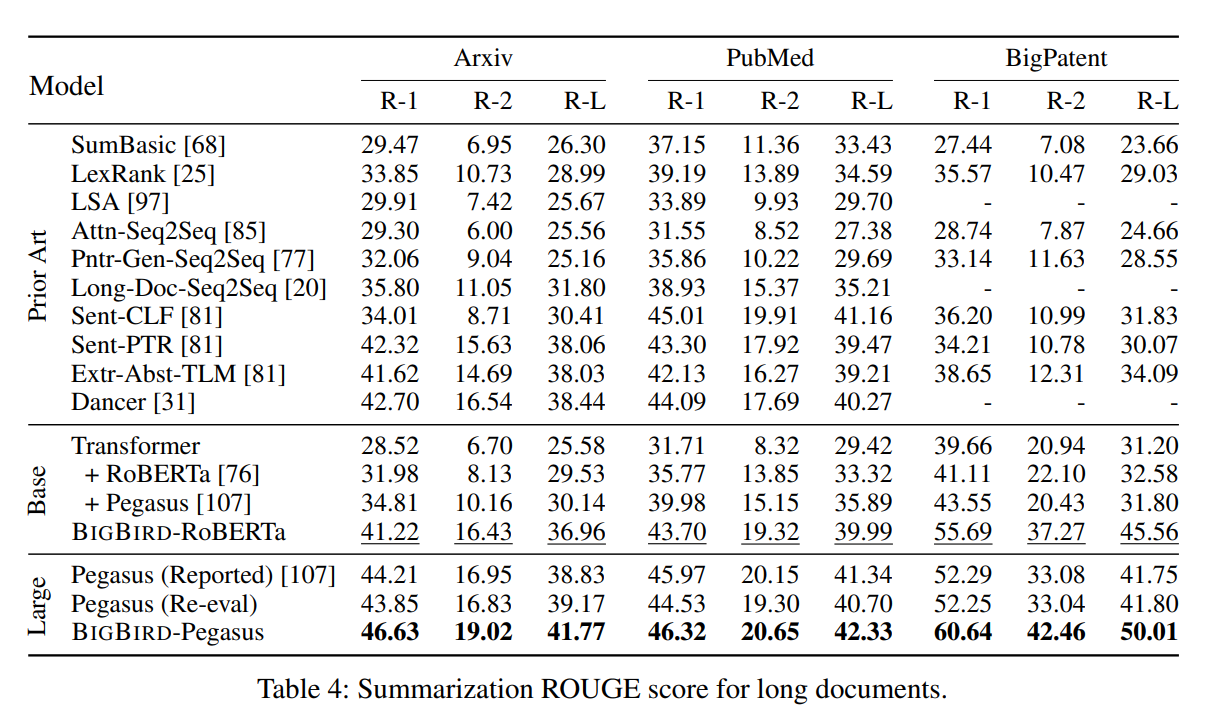
Conclusion
토큰의 수에 선형적인 sparse attention mechanism을 사용하는 BigBird를 제안함. seq2seq 함수의 universal approximator이고 Turing complete함. 이론적으로, global token을 추가해서 모델의 expressive power를 보존함. QA와 document classification와 같은 NLP task에서 SOTA 달성. 더 나아가 DNA에 대한 attention based contextual language model을 소개하고 promoter region prediction과 non-coding variants의 predicting effect와 같은 downstream task를 위해 미세조정함.