우선순위 큐
FIFO인 큐와 다르게 우선순위를 가지고 있어서, 우선순위가 높은 데이터부터 처리된다.
✅ 같은 우선순위를 가지면, 먼저 들어온 순으로 처리한다.
✅ 배열, 연결리스트, 힙(Heap) 모두 구현할 수 있지만 일반적으로는 시간복잡도가 적은 힙(Heap)을 사용함
💻 PriorityQueue 구현
from queue import PriorityQueue
q = PriorityQueue()
# 원소 삽입
q.put(3)
q.put(4)
q.put(1)
# 원소 삭제 및 반환
q.get() # 1힙 (Heap)
최댓값, 최솟값을 빠르게 연산하기 위한 완전 이진 트리
✅ 부모 노드의 값이 항상 자식 노드들의 값보다 크거나(Max Heap), 작아야(Min Heap) 함
📌 최소 힙(Min Heap)
루트 노드가 가장 작은 값을 가지며, 항상 부모 노드는 자식 노드보다 작은 값을 가짐 (부모 노드 >= 자식 노드)
💻 최소 힙 구현
import heapq
hq = []
# 삽입 - heapq.heappush(heap, item)
heapq.heappush(hq, 4)
heapq.heappush(hq, 1)
heapq.heappush(hq, 3)
heapq.heappush(hq, 7)
print(hq) # [1, 3, 4, 7]
# 삭제 - heapq.heappop(heap)
heapq.heappop(hq) # 1
📍 최소 힙으로 삽입, 삭제 과정 알아보기 !
삽입
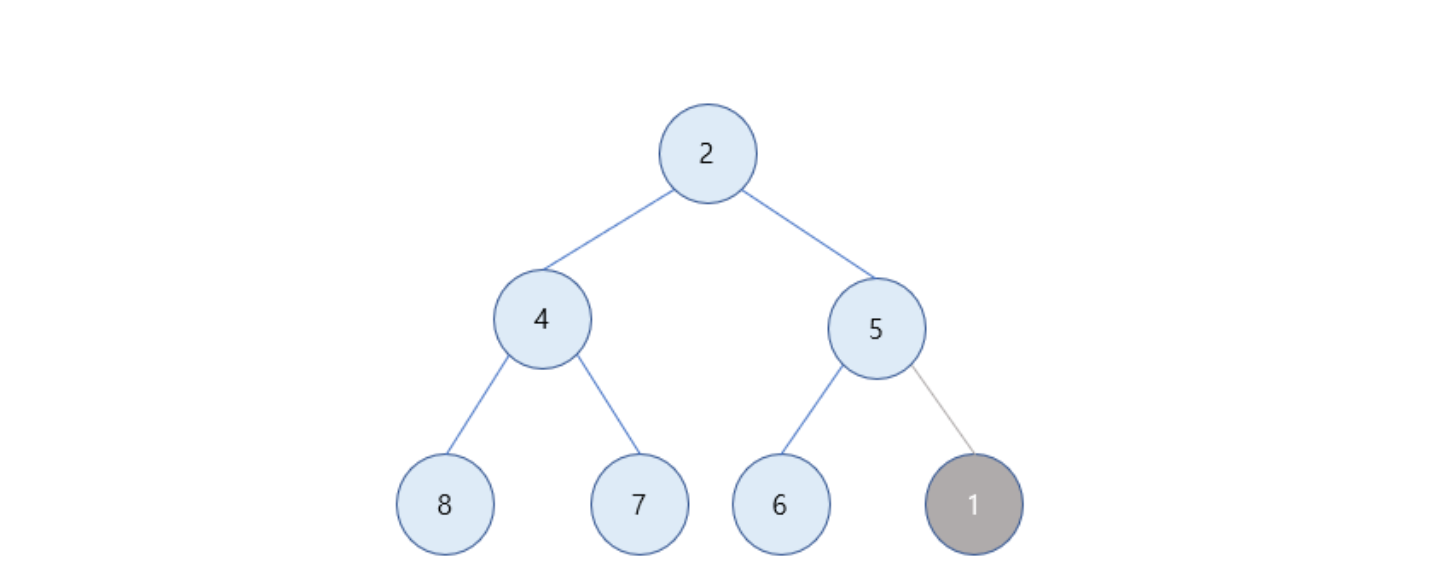
완전 이진 트리를 만족하는 노드에 1 삽입
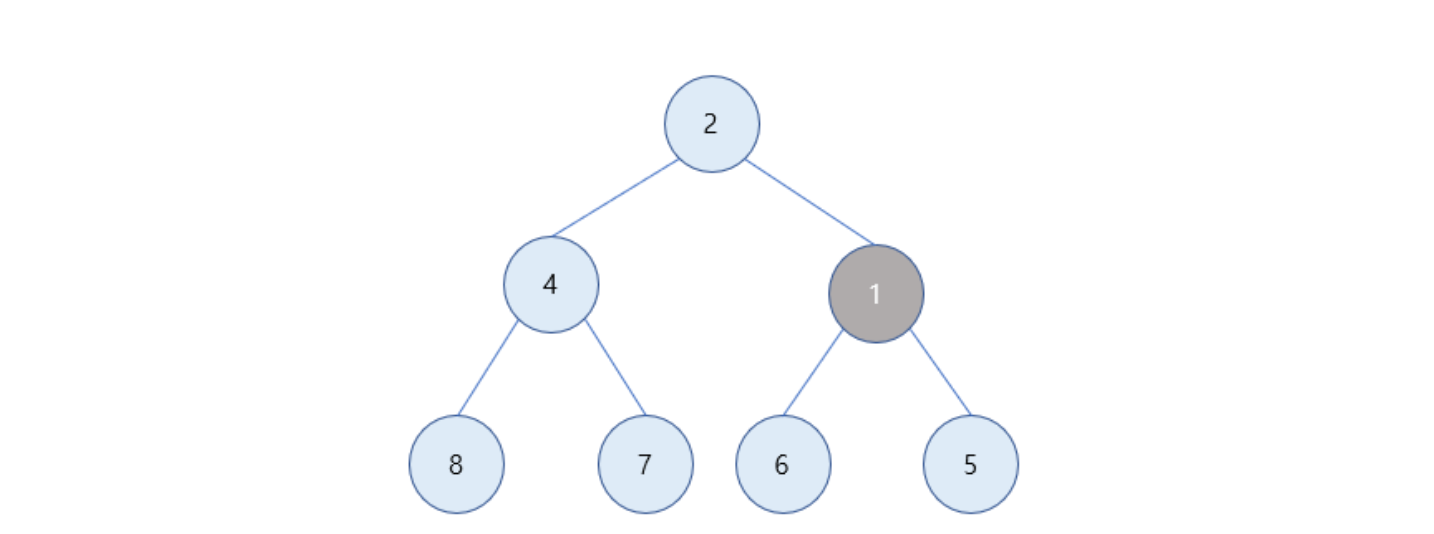
부모 노드인 5보다 1이 더 작으므로 최소 힙의 조건에 만족하도록 노드 위치 변경
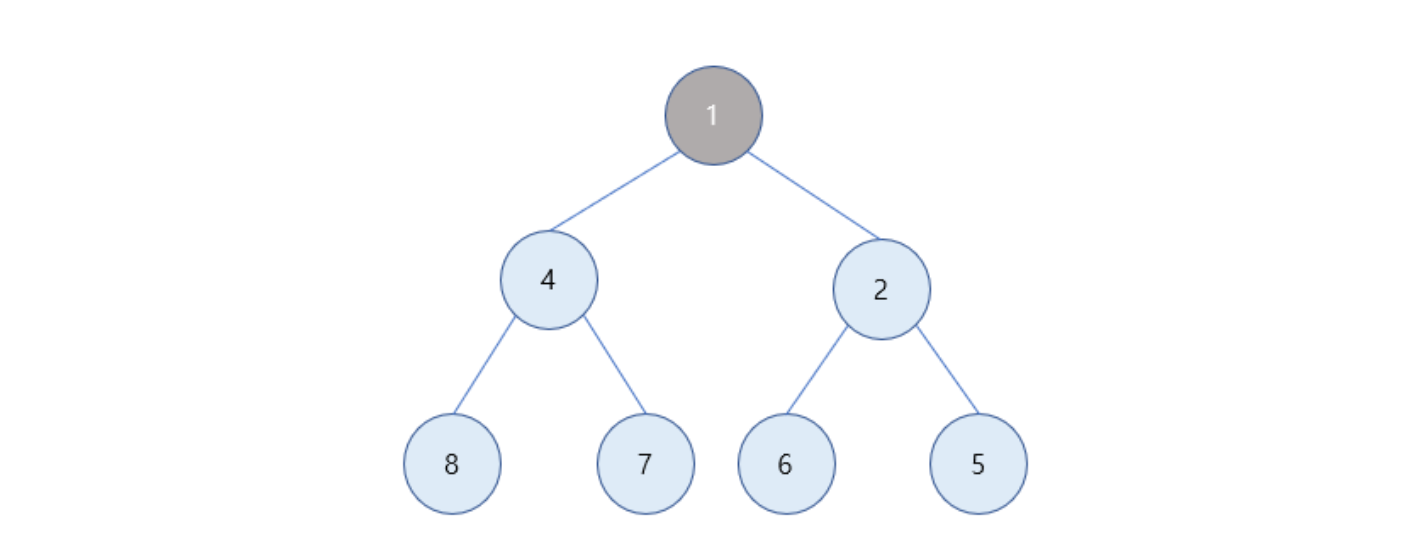
1이 부모 노드인 2보다 더 작으므로 위의 과정과 동일하게 노드 위치 변경
삭제
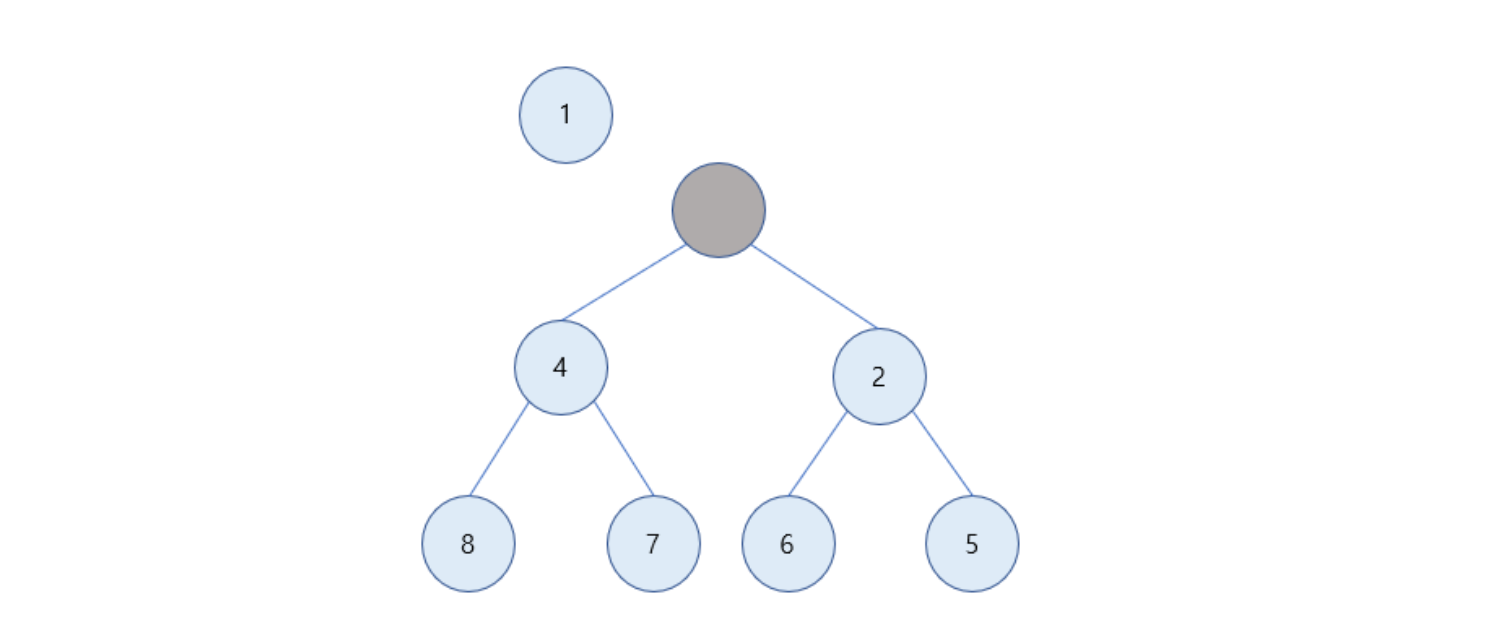
1을 삭제
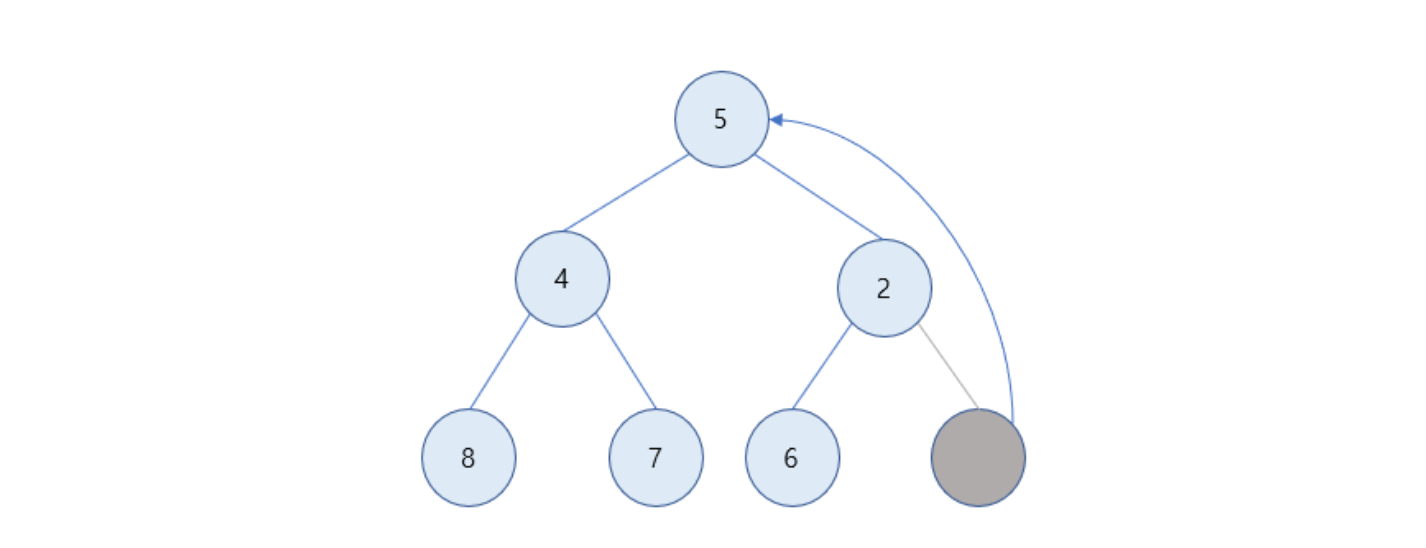
루트 노드가 비어있기 때문에 마지막 노드인 5로 채움
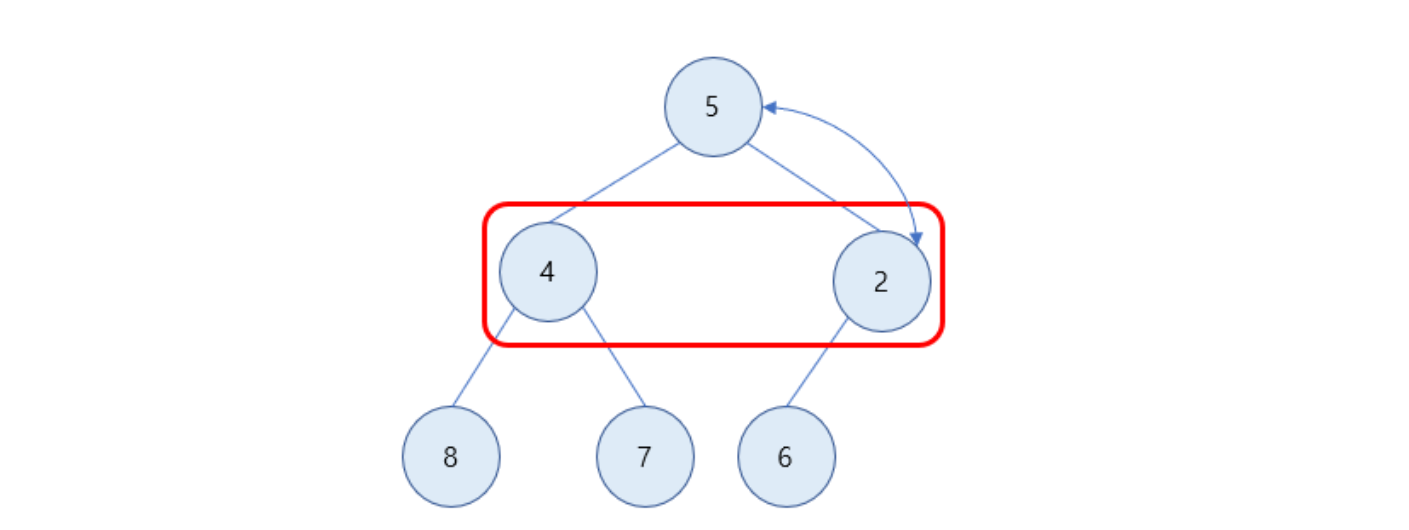
자식 노드인 2와 4가 5보다 더 작기 때문에 위치를 바꿔야 함.
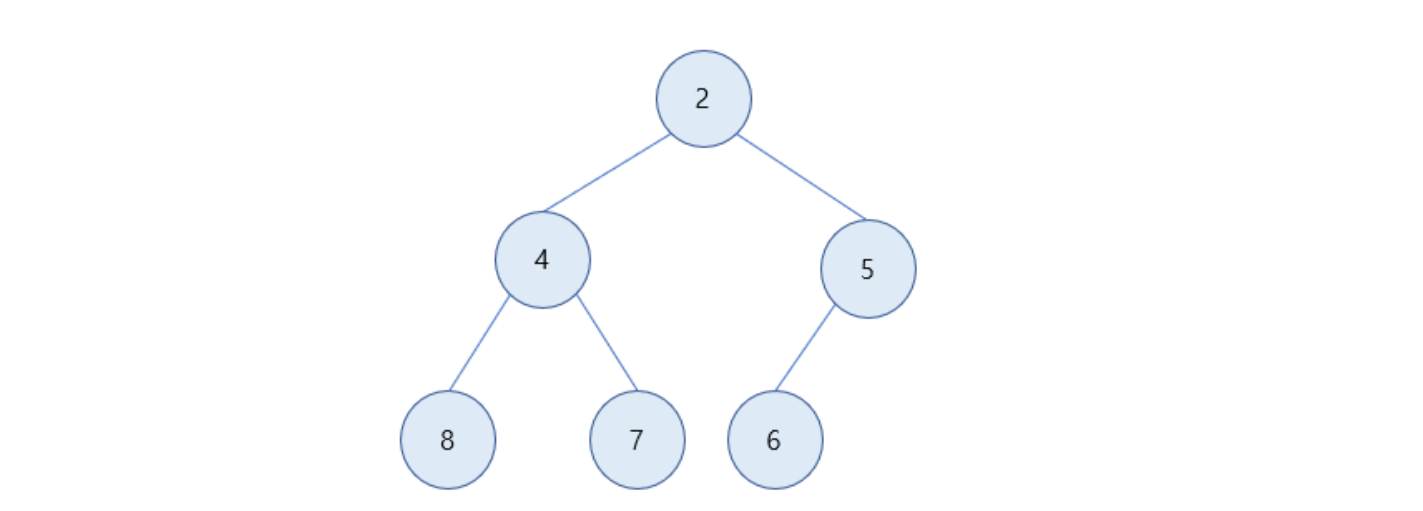
4보다 2가 더 작으므로 2와 노드 위치를 바꿔주고, 최소 힙의 조건에 만족하므로 삭제를 종료함.
✔ 삽입, 삭제의 시간복잡도
힙의 조건을 만족하도록 재배치하는 연산은 보통 힙의 높이(h)에 비례하여 시간이 소요되므로 데이터가 n개일때, 의 시간이 소요됨.
📌 최대 힙(Max Heap)
루트 노드가 가장 큰 값을 가지며, 항상 부모 노드는 자식 노드보다 큰 값을 가짐 (부모 노드 <= 자식 노드)
💻 최대 힙 구현
hq = [1, 3, 4, 7] # 위에서 구현한 기존 힙
max_heap = []
for item in hq:
heapq.heappush(max_heap, (-item, item))
print(max_heap)
-> [(-7,7), (-4,4), (-3,3), (-1,1)]
heapq.heappop(max_heap)[1] # 7
Reference

