08-1 합성곱 신경망의 구성 요소

[키워드]

합성곱

: 밀집층과 비슷하게 입력과 가중치를 곱하고 절편을 더하는 선형 계산

• 밀집층과 달리 각 합성곱은 입력 전체가 아니라 일부만 사용하여 선형 계산을 수행

합성곱 층의 필터

: 밀집층의 뉴런에 해당, 필터의 가중치와 절편을 커널이라고도 함

• 자주 사용되는 크기 (3, 3) 또는 (5, 5)
• 커널의 깊이는 입력의 깊이와 같음

특성맵

: 합성공 층이나 풀링 층의 출력 배열을 의미

• 필터 하나가 하나의 특성 맵을 만듦
• 합성곱 층에서 5개의 필터를 적용하면 5개의 측성 맵 만들어짐

패딩

: 합성곱 층의 입력 주위에 추가한 0으로 채워진 픽셀

• 패딩 사용 X -> 밸리드 패딩이라 함
• 합성곱 층의 출력 크기를 입력과 동일하게 만들기 위해 입력에 패딩을 추가
  -> 세임 패딩
  

스트라이드

: 합성곱 층에서 필터가 입력 위를 이동하는 크기

• 일반적으로 스트라이드는 1픽셀 사용

풀링

: 가중치가 없고 특성 맵의 가로세로 크기를 줄이는 역할을 수행

• 대표적으로 최대 풀링과 평균 풀링이 존재, (2, 2) 풀링으로 입력을 절반으로 줄임

합성곱

[dense의 뉴런 출력 과정]

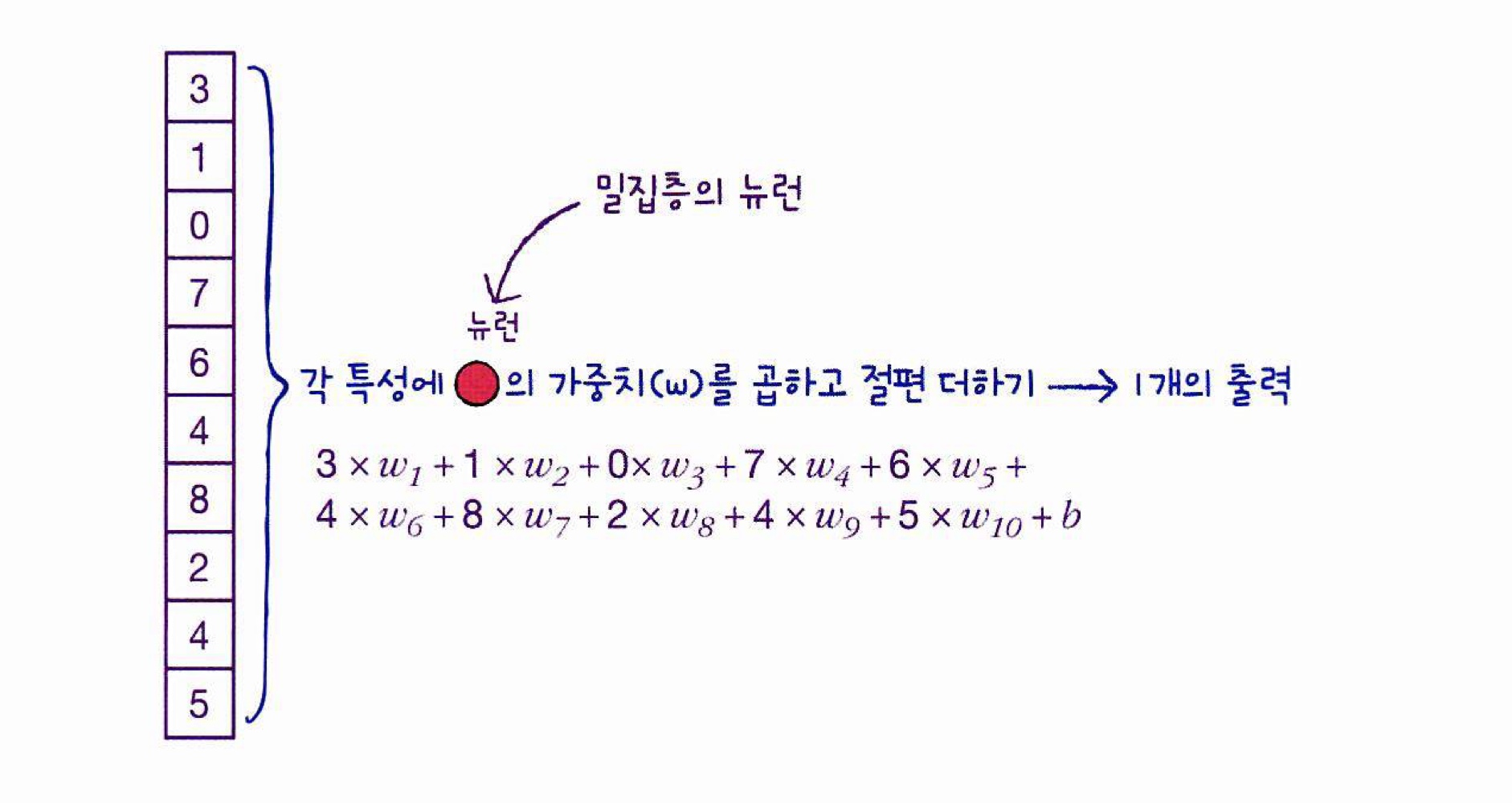
완전 연결 신경망 밀집층(dense)의 뉴런

• 인공 신경망에서는 가중치와 절편을 랜덤하게 초기화한 다음 에포크를 반복하면서 경사 하강법 알고리즘을 사용하여 손실이 낮아지도록 최적의 가중치와 절편을 찾아감

  	-> 이것을 '모델 훈련'이라 함

  ex) 밀집층에 뉴런이 3개 있다면 출력은 입력 개수와 상관없이 뉴런의 개수를 따라 3개이다.

합성곱 층의 뉴런

• 임의로 정한 가중치의 개수 만큼 특성과 곱해져 한 개의 출력을 만들고, 한 칸 이동하여 새로운 출력을 만듦
• 중요한 것은 첫번째 합성곱에 사용된 가중치와 절편이 두번째부터 끝까지 모든 합성곱에도 동일하게 적용되어야 한다는 점

convolutional의 뉴런 출력 과정

[convolutional의 뉴런 출력 결과]

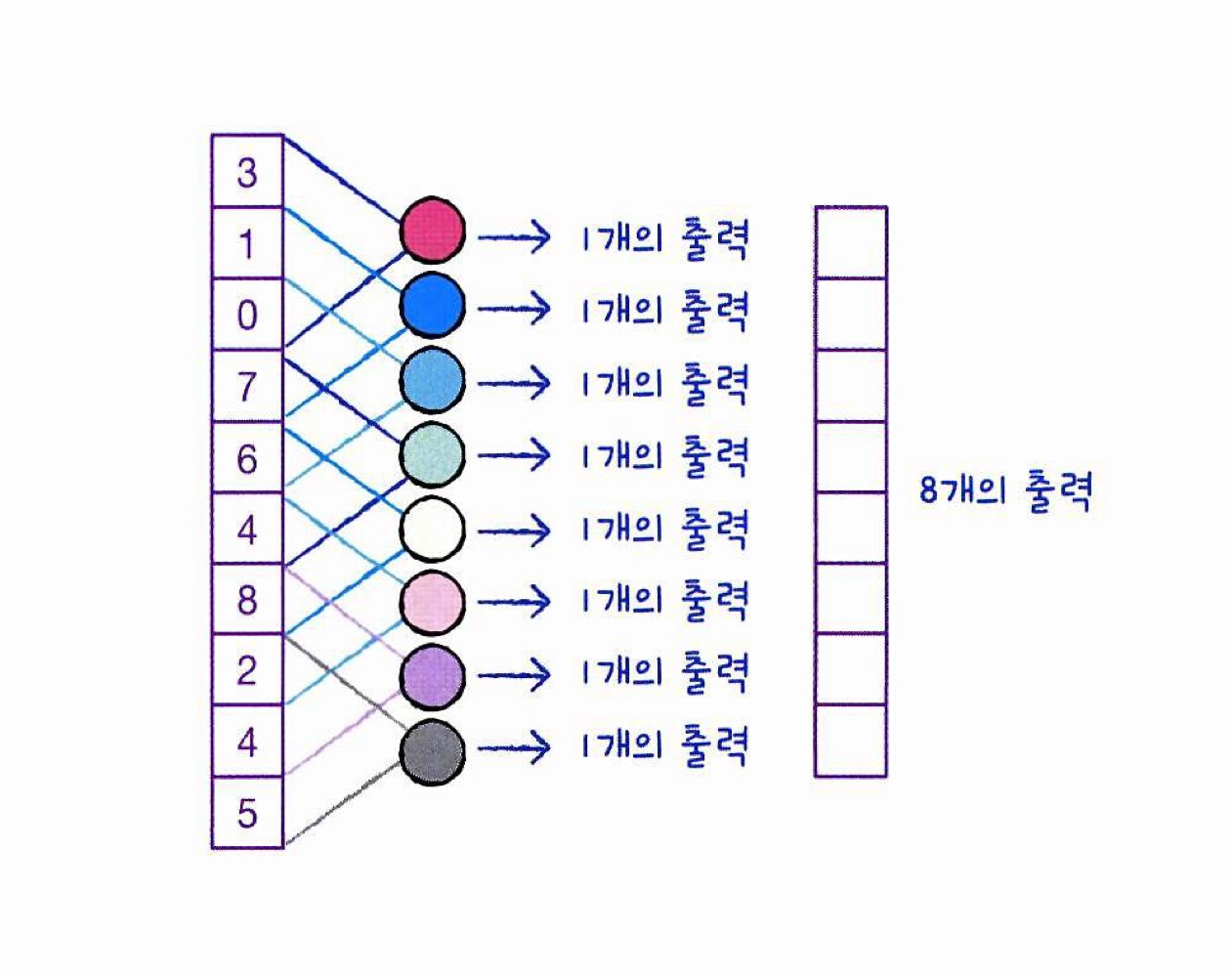
• 합성곱 신경망(convolutional neural network, CNN)에서는 완전 연결 신경망과 달리 뉴런을 filter 혹은 kernel이라고 부름
• 2차원에서도 합성곱층 적용이 가능, 입력이 2차원 배열이면 필터도 2차원이여야 함

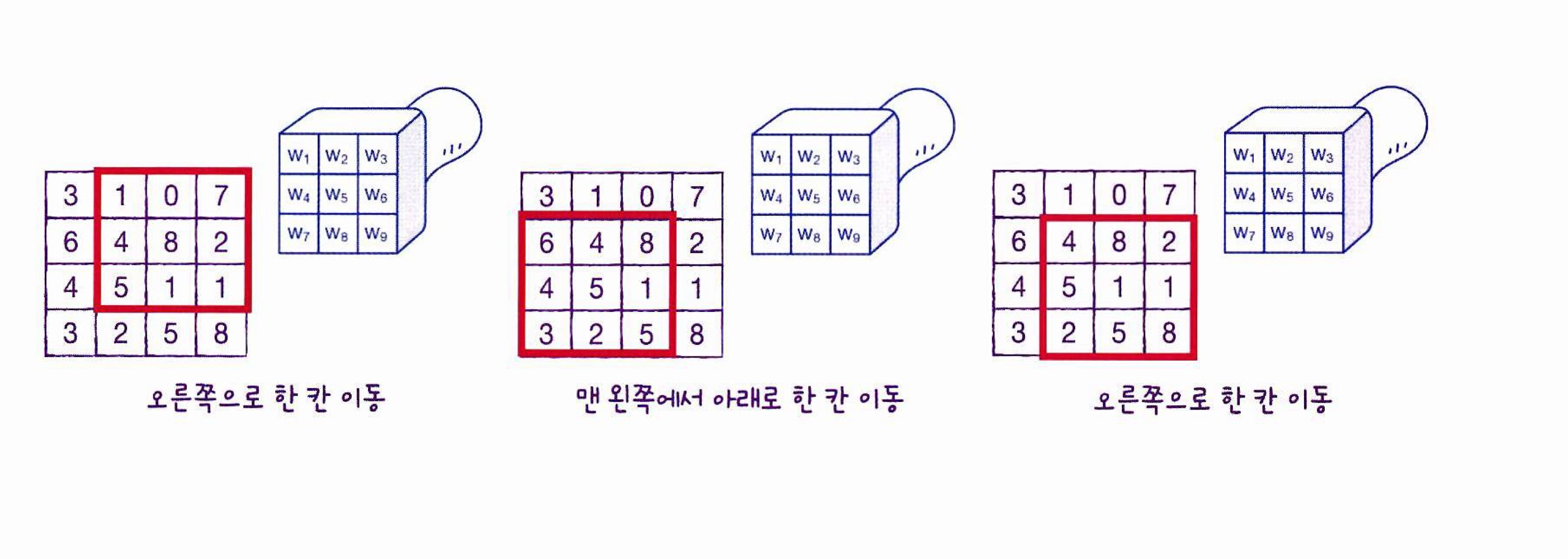
[2차원 배열 합성곱 출력 과정]

• 필터가 이동 가능한 횟수만큼 출력을 만들어낼 수 있고, 이러한 합성곱 계산을 통해 얻은 출력을 특성 맵(feature map)이라 함

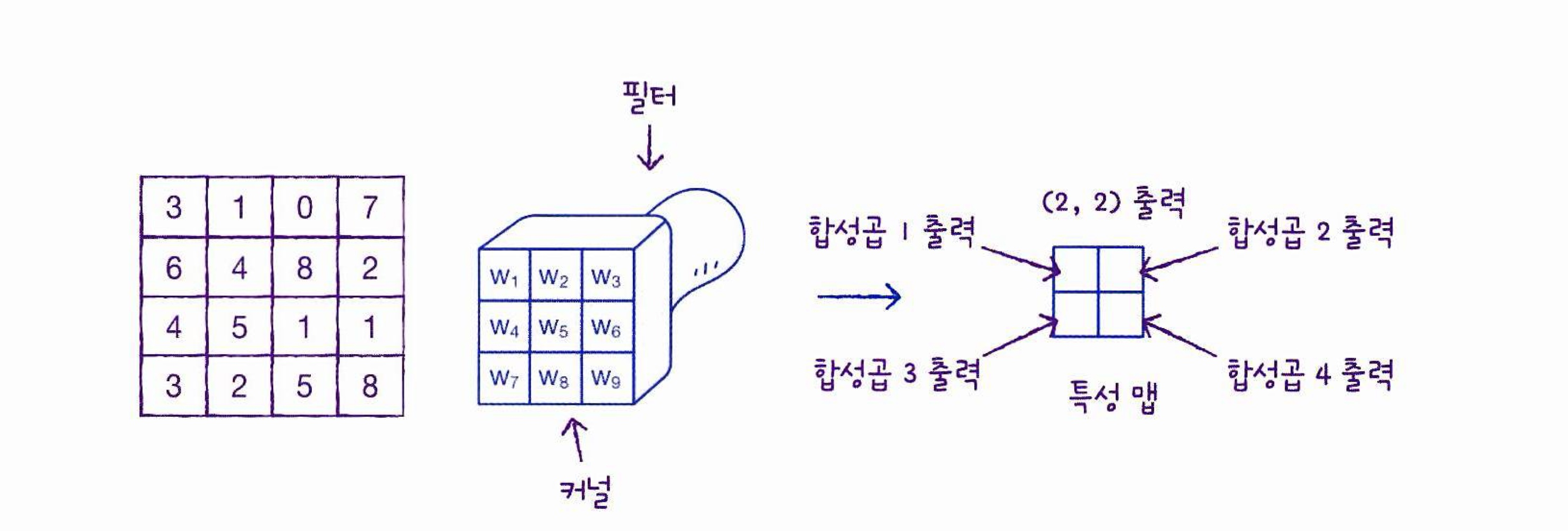
[2차원 배열 합성곱 특성 맵 출력]

• 합성곱 층에 있는 필터의 가중치(커널)을 다르게 하여 여러개의 특성 맵(출력)을 얻을 수 있음

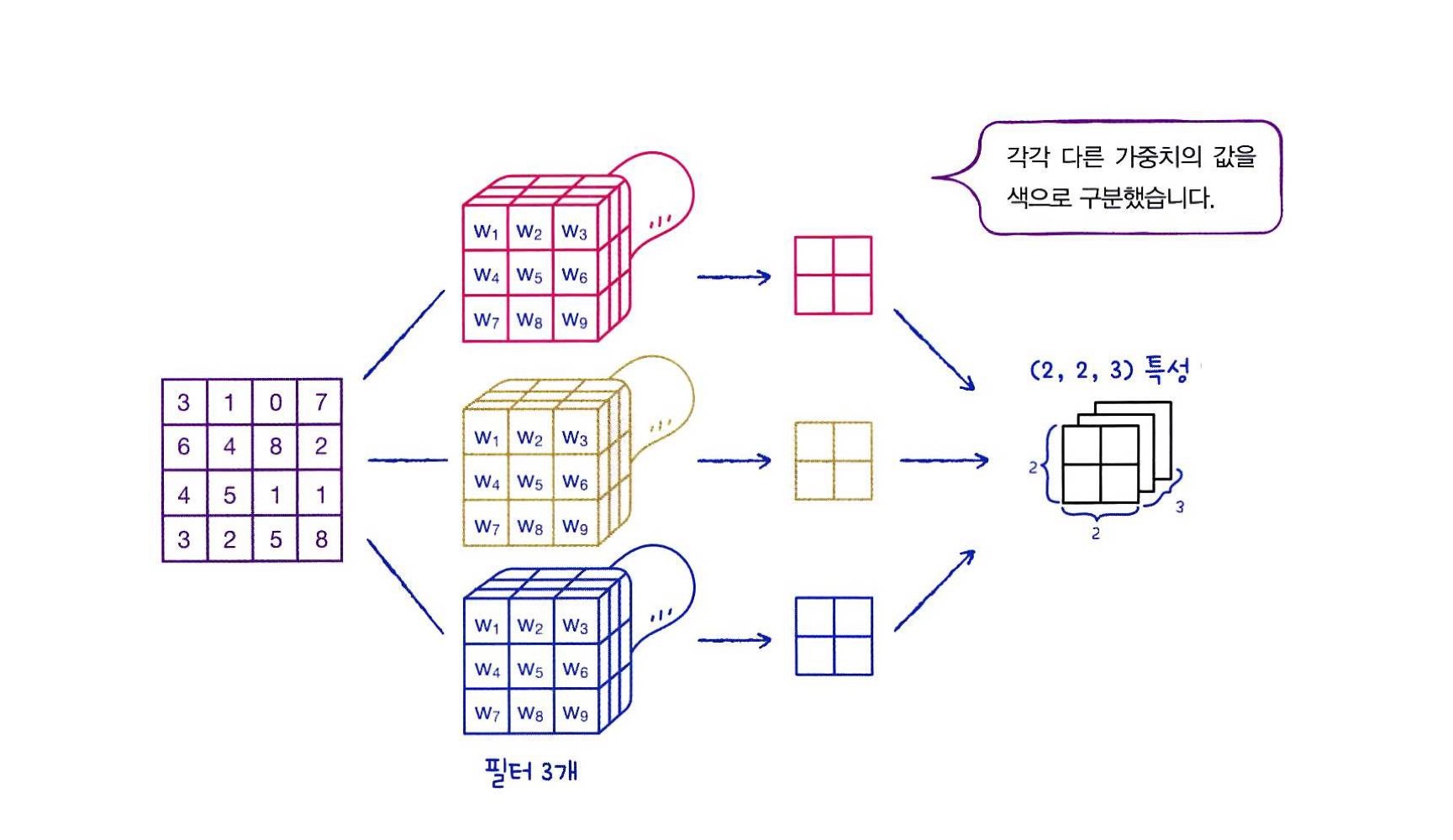
[여러개의 특성 맵으로 만들어지는 출력층]

케라스 합성곱 층

• Conv2D 클래스로 제공됨(왼쪽에서 오른쪽, 위에서 아래로 이동)
• 매개변수
  1) 필터의 개수(출력의 개수)
  2) 필터에 사용할 커널 크기(kernel_size = ), 보통 (3, 3) 이나 (5, 5) 사용
  3) 활성화 함수(activation = )
  

from tensorflow import keras
keras.layers.Conv2D(10, kernel_size=(3,3), activation='relu')

패딩(padding)

• (4,4) 크기의 입력에 (3,3) 크기의 커널을 활용하여 출력의 크기를 (2,2)가 아닌 (4,4)로 만드려면?
  -> 실제 입력 크기는 (4,4)이지만 입력 배열의 주위를 가상의 원소를 만들고 0으로 채워서 (6,6)인 입력으로 만든다.

  -> 이 과정을 패딩(padding)이라고 함

  
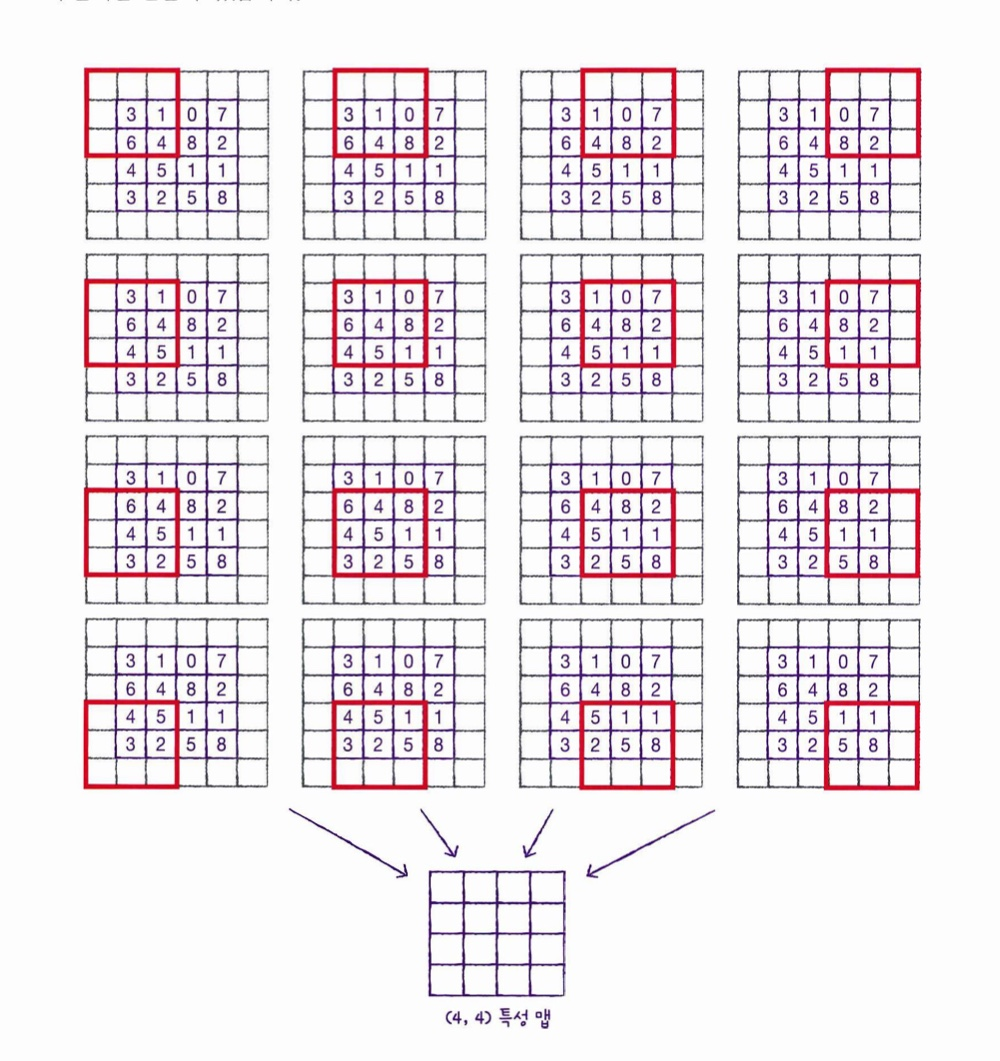
  [패딩을 활용한 특성 맵 출력]

• 패딩의 종류

  세임 패딩(same padding):
  입력과 특성 맵의 크기를 동일하게 만들기 위해 입력 주위에 0 으로 패딩하는것.
  합성곱 신경망에서는 이 방법이 자주 사용됨.

  밸리드 패딩(valid padding) :
  패딩없이 순수 입력 배열에서만 합성곱을 하여 특성 맵을 만드는 방법으로 특성 맵의 크기가 줄어든다.

• 패딩을 사용하는 이유?
  : 만약 패딩이 없다면 입력의 모서리 값은 필터를 통과하는 경우가 중앙 값에 비해 현저히 적기때문에 패딩을 통해 모서리에 있는 정보도 특성 맵으로 잘 전달될 수 있도록 해준다.

-> 적절한 패딩은 이미지의 가장자리에 있는 정보를 잃어버리지 않도록 도와준다.

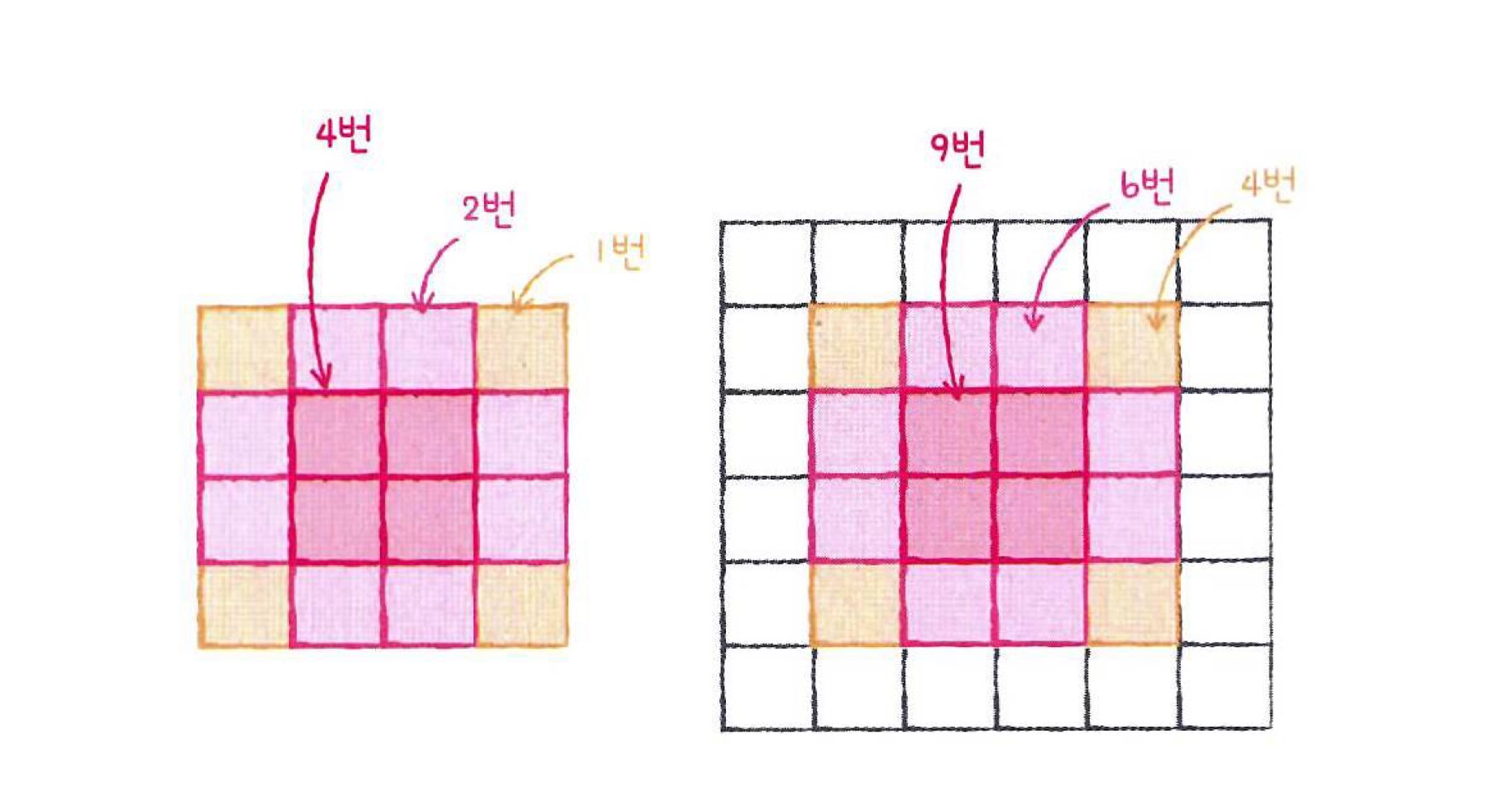
[패딩을 사용하여 모서리 정보의 필터 통과 횟수를 증가시킴]

[케라스를 통한 패딩 사용]

keras.layers.Conv2D(10, kernel_size=(3,3), activation='relu', padding='same')

스트라이드(stride)

• 커널의 이동을 한 칸에서 두 칸으로 늘리면 그만큼 특성맵의 크기도 작아짐
  -> 스트라이드(stride)라 함

# stride의 기본값은 1이다.
keras.layers.Conv2D(10, kernel_size=(3,3), activation='relu', padding='same', strides=1)

풀링(pooling)

• 합성곱 층에서 만든 특성 맵의 가로세로 크기를 줄이는 역할을 함
  -> 특성맵의 개수는 줄이지 않음
  

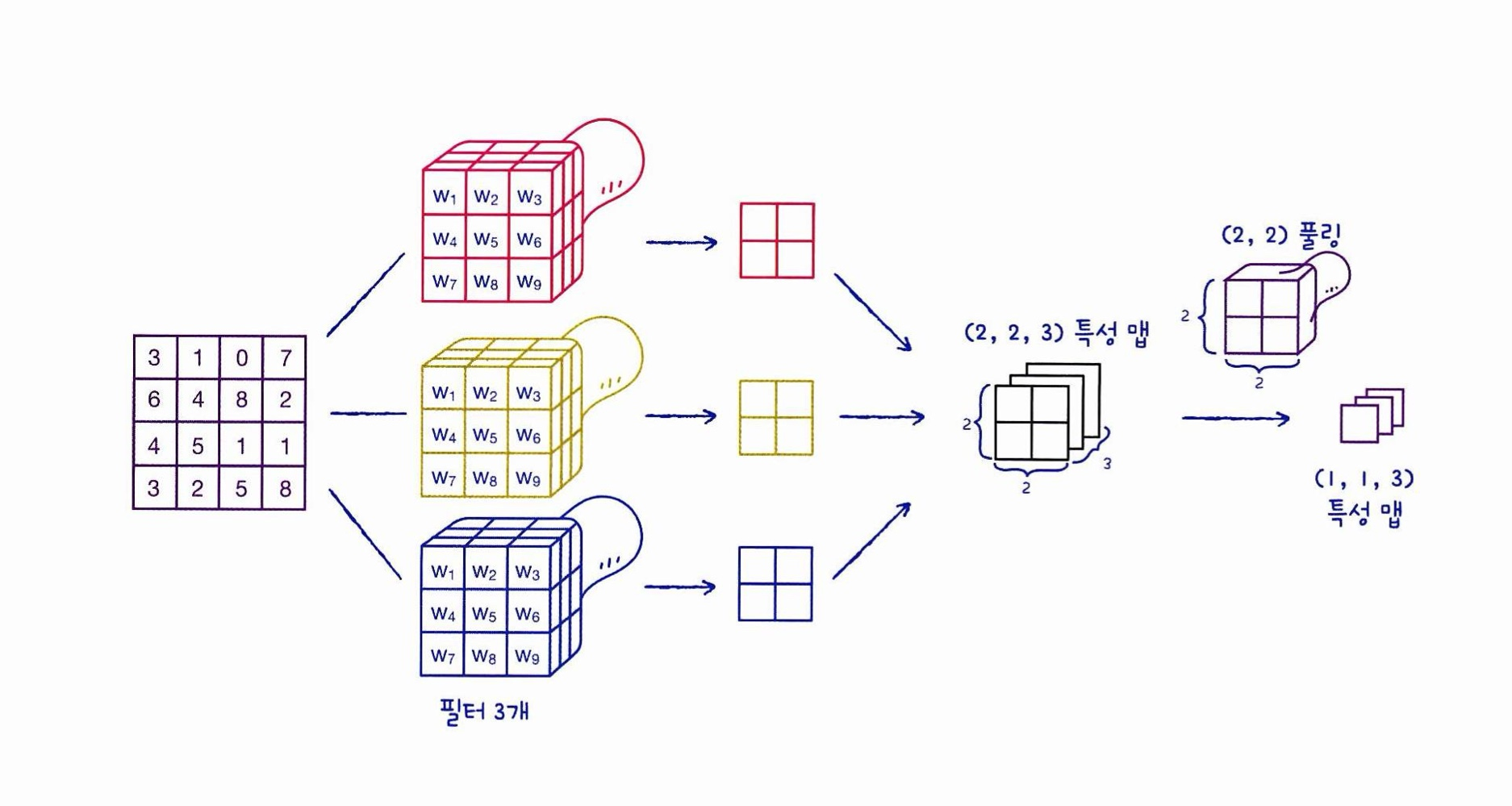
[풀링을 포함한 합성곱 층 생성 과정]

• 풀링의 종류
  : 풀링 또한 합성곱처럼 입력 위를 지나가면서 필터링함
  -> 풀링에는 가중치X, 필터링 영역에서 특정 값을 고름

  최대 풀링(max pooling) : 가장 큰 값을 선택
  keras.layers.MaxPooling2D() 사용

  평균 풀링(average pooling) : 평균 값을 선택
  keras.layers.AveragePooing2D() 사용
  -> 평균을 통해 특성 맵의 중요 정보를 희석시킬 수 있기 때문에 잘 사용하지 않음

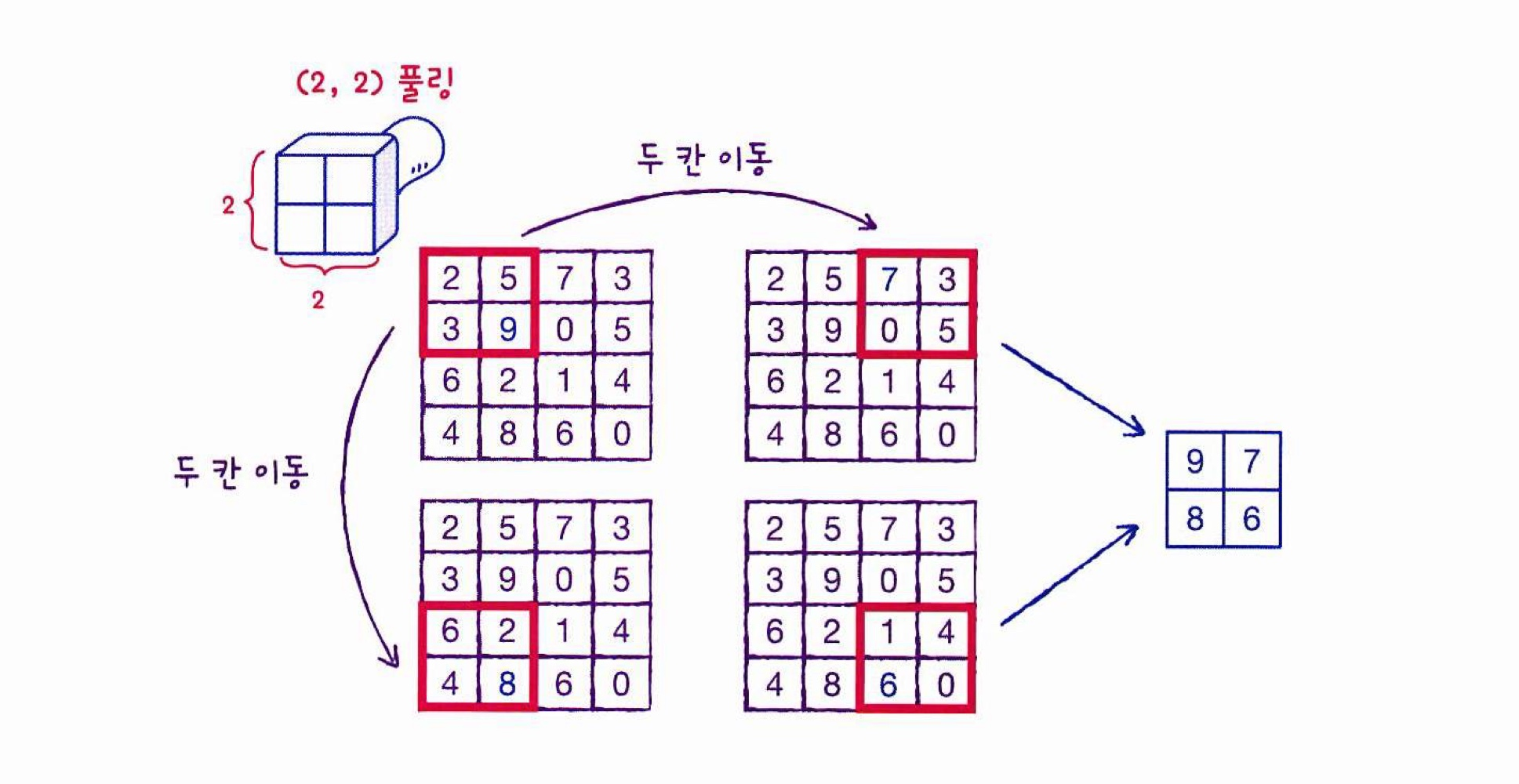
[(2, 2) 최대 풀링 적용]

• 풀링 영역은 합성곱 층 커널 이동과는 다르게 겹치지 않고 이동한다.
  -> 스트라이드가 2
  ex) (3, 3) 풀링이면 가로세로 세 칸씩 이동

• 매개변수
  1) 풀링의 크기 : 대부분 2로 설정하여 가로세로 크기를 절반으로 줄인다.
  가로세로 방향의 풀링 크기를 정수 튜플로 지정할 수 있으나, 극히 드물다.
  2) stride : 기본값이 자동으로 풀링의 크기로 설정되므로 따로 지정할 필요는 없다.
  3) padding : 기본값은 valid로 패딩을 하지 않는다. 이 매개변수를 바꾸는 경우는 거의 없다.
  

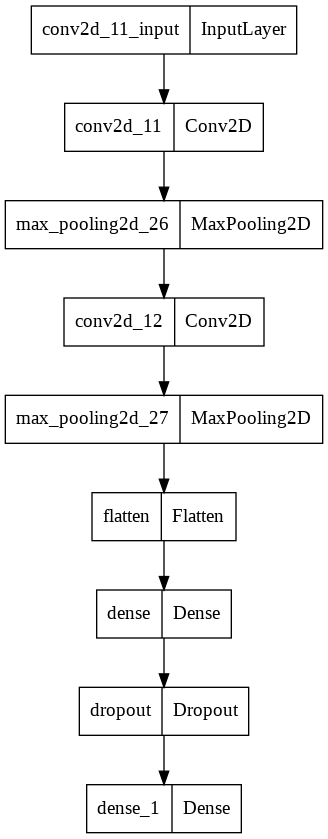
합성곱 신경망 구조

< 입력 크기 = (4,4) / 필터 개수 = 3 / 합성곱층 커널 = (3,3) / padding = same 의 합성곱 신경망 구조>

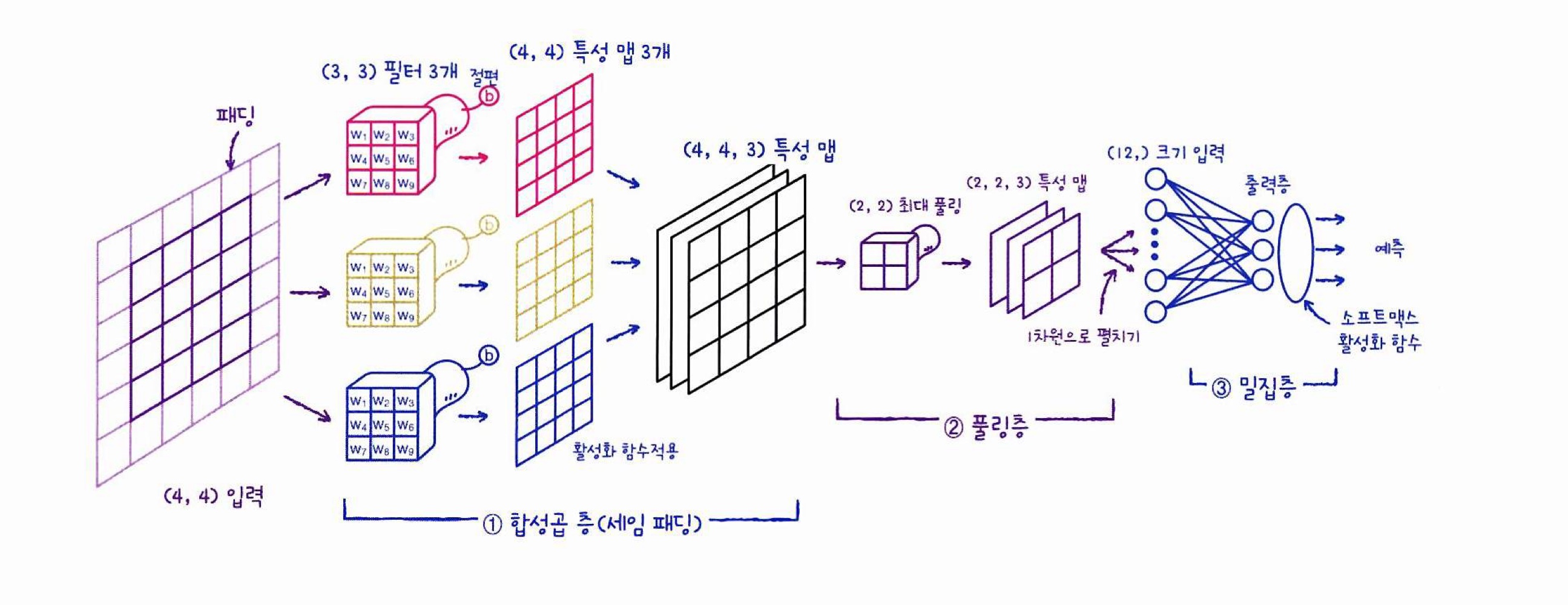
• 합성곱의 필터가 (3,3) 3개 이므로 각각 (3,3) 크기의 가중치를 가지고 있으며 필터마다 절편이 하나씩 있다.

• 추가적인 설정이 없으면 패딩은 텐서플로에서 자동으로 추가하므로 세임 패딩,
  스트라이드는 1이기에 특성 맵의 크기는 입력과 동일한 (4,4)이다.

• 모든 필터로 만들어진 특성 맵을 합쳐 (4,4,3) 특성 맵이 만들어 진다.

• 최대 풀링을 사용하여 특성 맵의 크기를 절반으로 줄여 특성맵은 (2,2,3)이 된다.

• 마지막으로 Flatten 클래스를 이용하여 (2,2,3)을 (12)의 1차원 배열로 변경하여 출력층(dense)의 입력으로 나타낸다.

<풀링 사용하는 이유>
: 합성곱에서 스트라이드를 크게하여 특성 맵을 줄이는 것보다 풀링층에서 줄이는 것이 더 나은 성능을 내기 때문

컬러 이미지를 사용한 합성곱

• 패션 MNIST 데이터는 흑백 이미지이기에 2차원 배열로 표현할 수 있음
  -> 컬러이미지는 RGB로 구성되어 있기에 3차원 배열로 표현
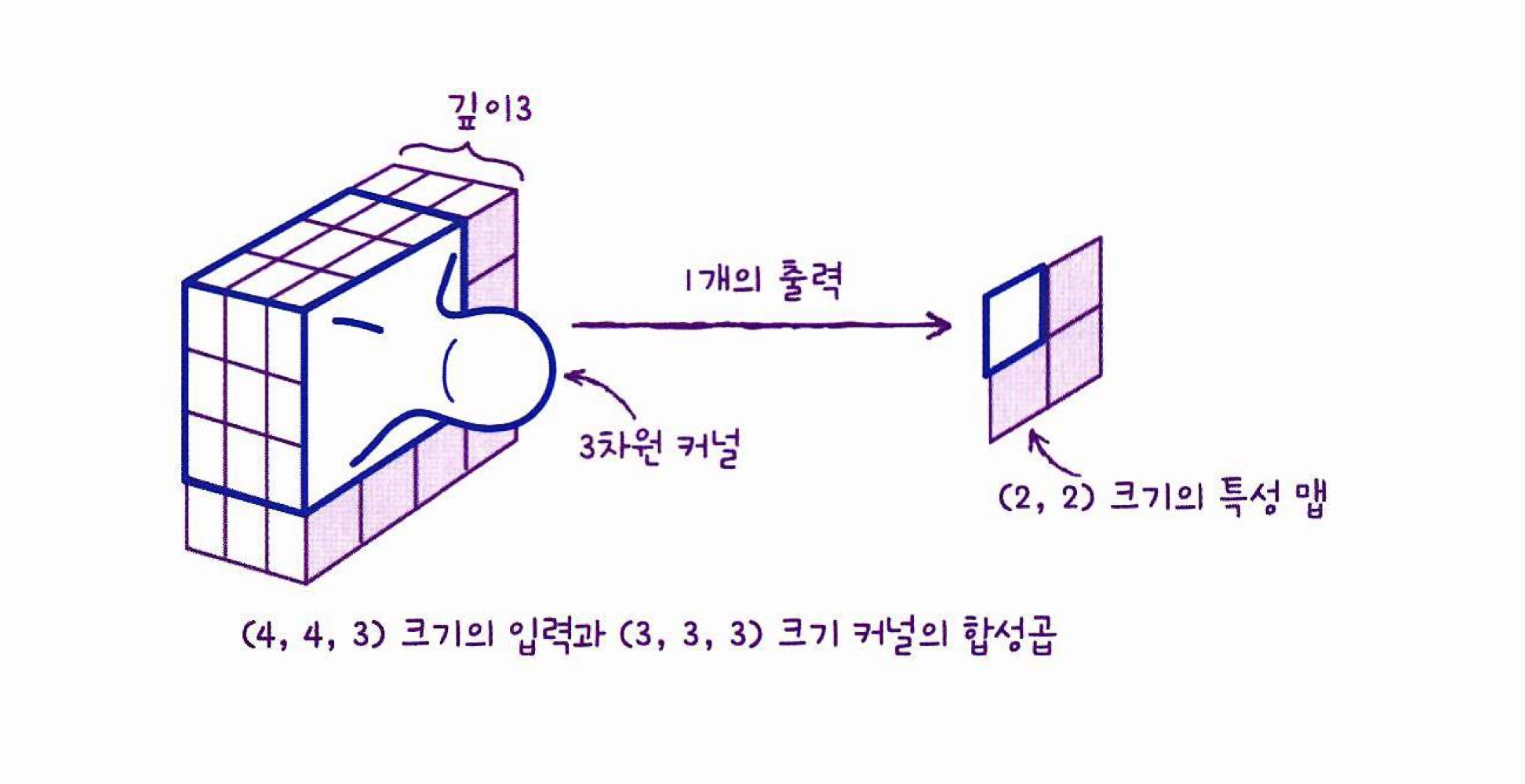
  ex) 입력이 (4, 4, 3)으로 전달됨
  

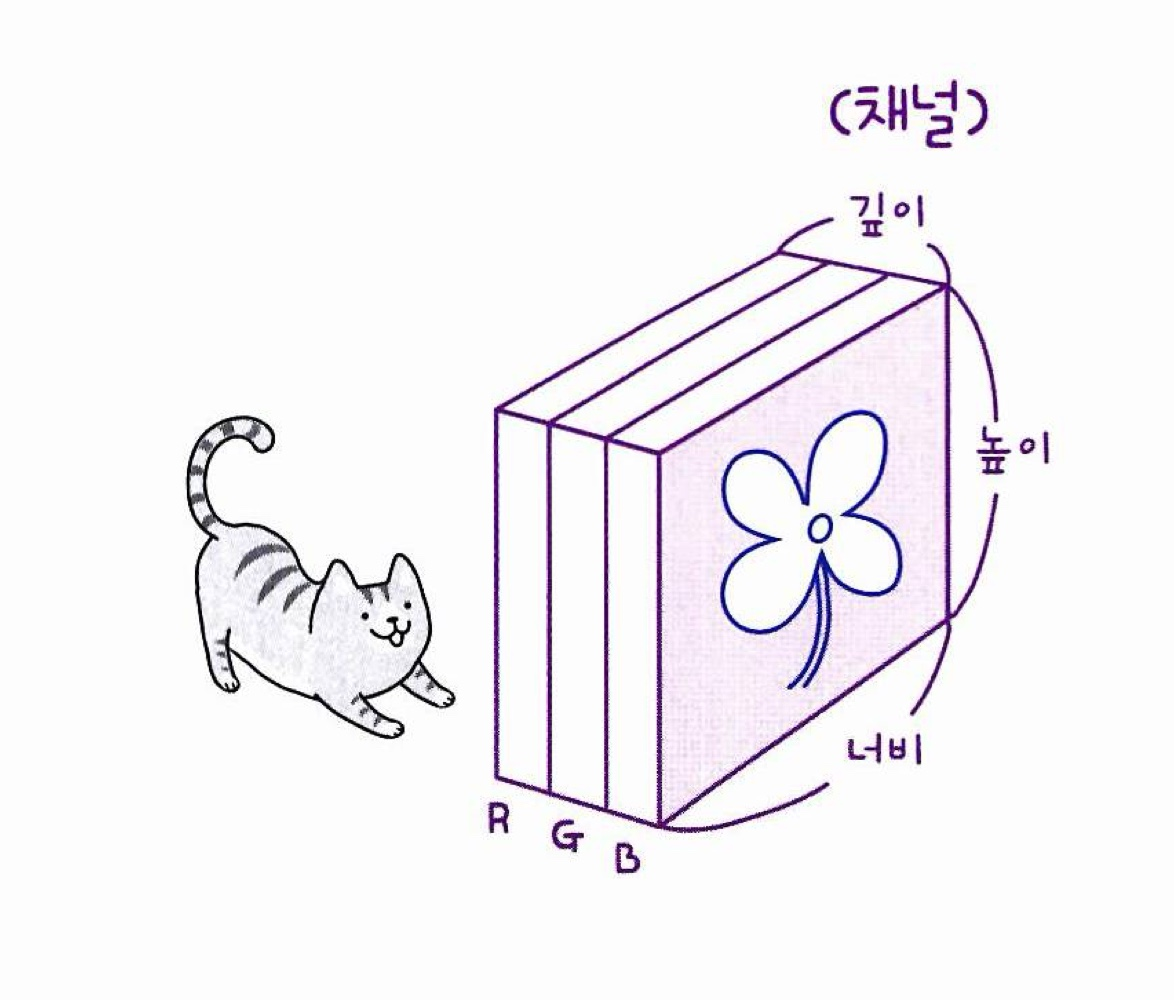
• 깊이가 있는 3차원 필터를 사용하여 합성곱을 진행
  : 이때 커널의 크기는 (3,3,3)이 되며 이 합성곱의 계산은 27개의 원소에 27개의 가중치를 곱하고 절편을 더하는 방식
  

• 입력이나 필터의 차원이 몇개인지 상관없이 2차원 합성곱과 같이 항상 출력은 하나의 값이고, 이 값이 특성 맵에 있는 하나의 원소가 되는 것

• keras 합성곱 층은 할상 3차원 입력을 원함
  -> 따라서 패션 MNIST 데이터처럼 흑백이미지의 경우 깊이 차원에 1을 추가한 3차원 배열로 변환하여 전달

• 합성곱층 - 풀링층 다음에 다시 또 합성곱 층이 오는 경우
  

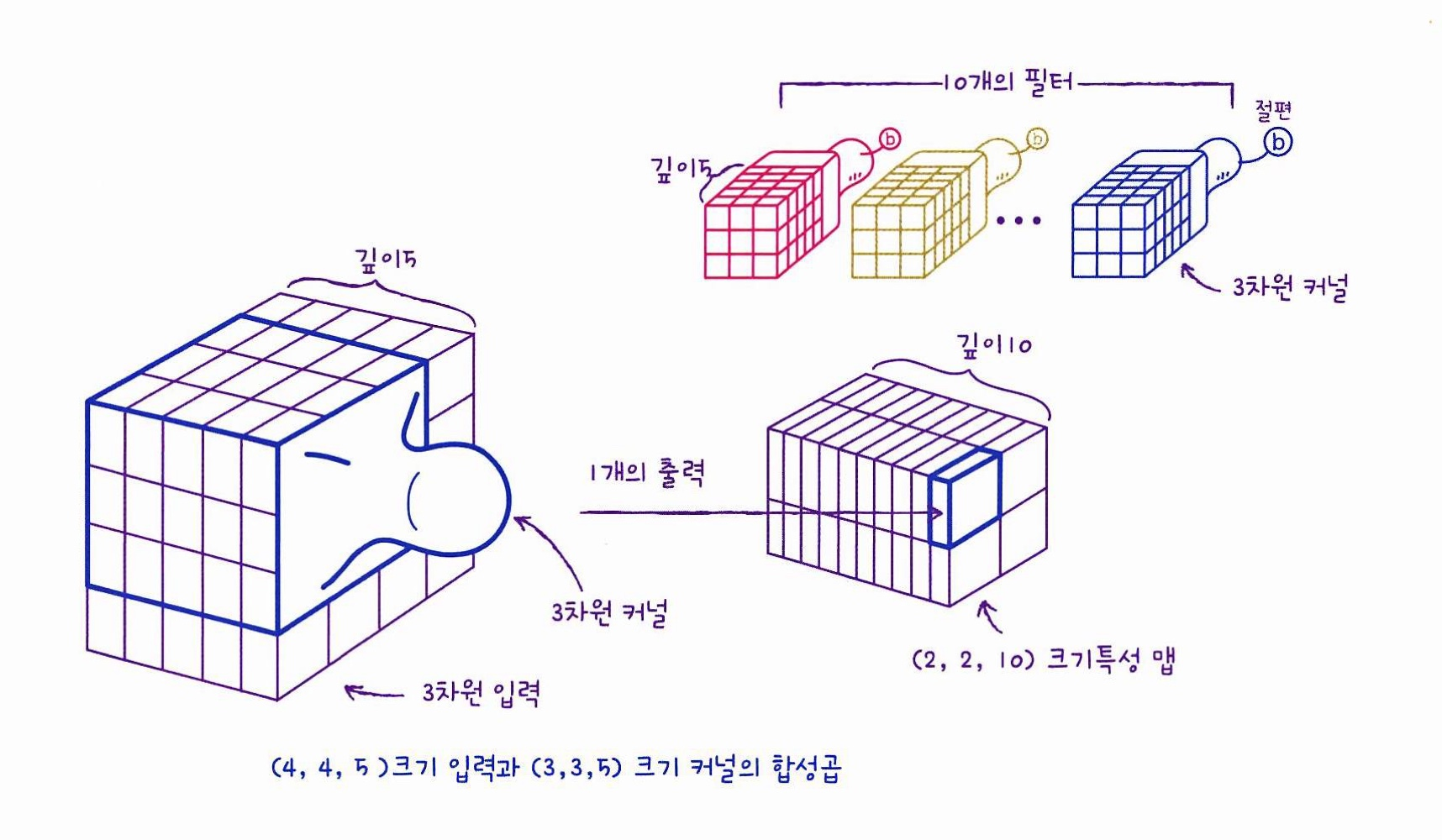
• 첫번째 합성곱 층-풀링 층을 통과한 특성 맵의 크기가 (4,4,5)라면,
  두번째 합성곱 층의 필터의 너비와 높이가 각각 3일때, 필터의 커널은 (3,3,5)가 된다. 따라서 하나의 필터는 335 = 45개의 가중치를 곱하고 절편을 더한 1개의 출력을 만든다.

• 이 과정을 통해 두번째 합성곱 층의 필터 개수가 10개라면 특성맵의 크기는 (2,2,10)이 된다. 그리고 마지막에 특성 맵을 모두 flatten하여 dense층의 입력으로 사용한다.

*합성곱 신경망은 너비와 높이는 점점 줄어들고 깊이는 점점 늘어나는 것이 특징

08-2 합성곱 신경망을 사용한 이미지 분류

패션 MNIST 분류 모델 생성

패션 데이터 불러오기

• 데이터 불러와서 훈련, 검증, 테스트 셋 나누고, 정규화함

from tensorflow import keras
from sklearn.model_selection import train_test_split

# fashion mnist data set 불러오기
(train_input, train_target), (test_input,test_target) = keras.datasets.fashion_mnist.load_data()

# 정규화
train_scaled = train_input.reshape(-1,28,28,1) / 255.0   # reshape(-1,28,28) : (48000, 28, 28)을 (-1(개수 알아서 맞춰라), 28(행), 28(열), 1(두께))로 바꾸어라

# 훈련 셋에서 검증 셋 나누기
train_scaled, val_scaled, train_target, val_target = train_test_split(train_scaled, train_target, test_size = 0.2, random_state=42)

• 결과
  하나의 이미지에 대한 깊이(채널) 차원을 넣어주어 (48000,28,28) 크기인 train_input(3차원 배열)이 (48000,28,28,1) 크기인 train_scaled(4차원 배열) 되었다.
  

합성곱 신경망 만들기