Outline

• linear regression
• locally weighted regression
• probability intepretation
• logistic regression
• newton's method

지난 시간에 linear regression에 대해 배웠다. 오늘은 여기서 개념적으로 발전한 locally weighted regression을 배울 것이다. 이와 함께 저번 시간에 왜 mean "square" error를 사용하는 지에 대해서도 질문을 했는데, 이 질문에 답하기 위해 확률적인 이야기를 가져올 것이다. 그리고 더 나아가 logistic regression 을 배울 것이고, 이 회귀 문제를 풀기 위한 newton's method를 설명할 것이다.

Locally weighted regression

Parametic and non-parametic

learning 에는 두가지 종류가 있다.

• "parametic" learning algorithm
  
• "non - parametic" learning algorithm

parametic한 알고리즘은 고정된 parameter들을 데이터에 맞추는 형식이다.
linear regression이 그 대표적인 예시인데, 우리가 가설을 미리 설정해두면 데이터에 fit 되도록 가설의 parameter들을 조정한다.
Assumption 하다고도 표현하는데, 예를 들어 linear regression 에서 우리는 독립변수와 종속변수 사이의 관계가 linear 하다고 가정하고, 잔차가 normal distribution을 따른다고 가정한다(뒤에 설명) 이렇게 데이터가 어떤 분포를 따른다고 가정하는 것을 "모수적" 이라고 한다.
이 알고리즘은 데이터를 계속해서 저장해둘 필요가 없기 때문에 메모리를 적게 사용한다.

non-parametic 한 알고리즘은 parametic과 달리 데이터의 분포에 대해서 strong 한 assumption을 하지 않는다. "비-모수적" 이라고 표현한다. 오해하지 말아야 할 것은 비-모수적 이라는 것은 assumption하지 않다는 것이지, assumption 이 전혀 없다는 뜻은 아니다. 비교적 그 assumption이 약하고 거의 없다고 가정 한다고 보는게 맞다. 이 알고리즘은 데이터를 계속 누적해서 저장해야 하기 때문에 메모리를 많이 사용한다. 데이터를 계속 누적해서 저장해야 하는 이유는 데이터의 분포를 가정하지 않은 상태이기 때문이라고 볼 수 있다.

parametic-learning algorithm : 데이터가 어떤 분포를 따른다고 가정한 알고리즘
non-parametic-learning algorithm : 데이터가 어떤 분포를 따른다고 거의 가정하지 않은 알고리즘

linear to locally weighted

linear regression 에서는 가설을 미리 설정해 뒀어야 했다. 그러나 데이터가 어떤 분포일 지 미리 가정하는 것은 상당히 어려운 일이다. 이러한 과정을 자동으로 해주는 것을 feature sellection algorithm 이라고한다.

$h(x) = \theta_0+\theta_1x$ 으로 설정할 수도 있고
$h(x) = \theta_0+\theta_1x^2+\theta_2\sqrt{x}$ 로 설정할 수도 있다.
그러나 어떤 가설이 더 좋은 지는 해보기 전에는 알 수 없고 이를 정하기도 어려운 일이다.

locally weighted algorithm 은 이러한 문제를 해결한다.

간단하게 설명하면, locally weighted algorithm은 자기로부터 멀리 있는 데이터는 관심을 적게 주고 가까이 있는 데이터에게는 관심을 많이 주는 방식이다.

다음과 같은 데이터 셋이 있다고 하자

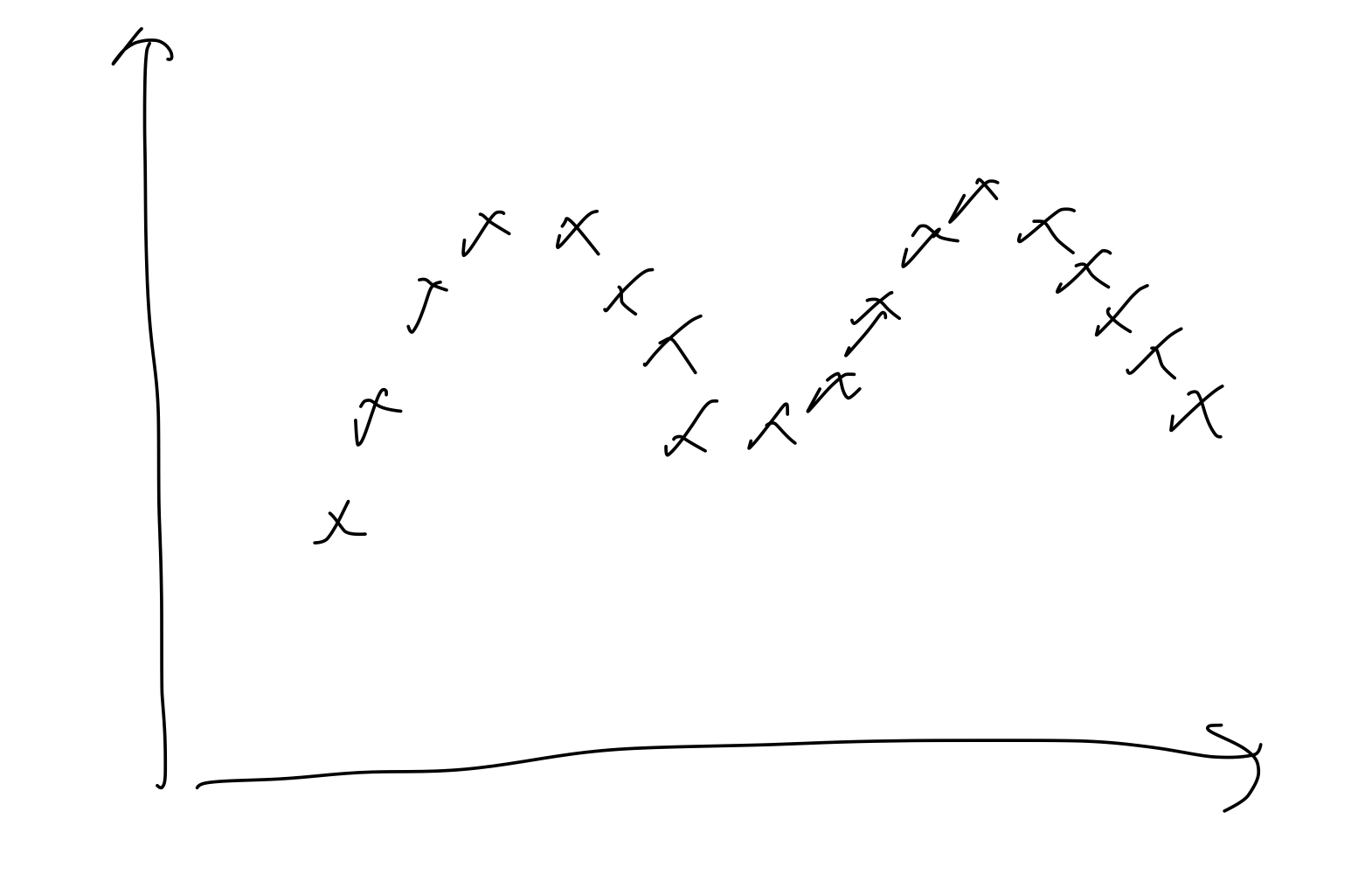
linear regression 에서는 정해진 $h_\theta(x)$에 대하여 $J(\theta)(MSE)$ 를 최소화 하는 방향으로 선을 긋는다.

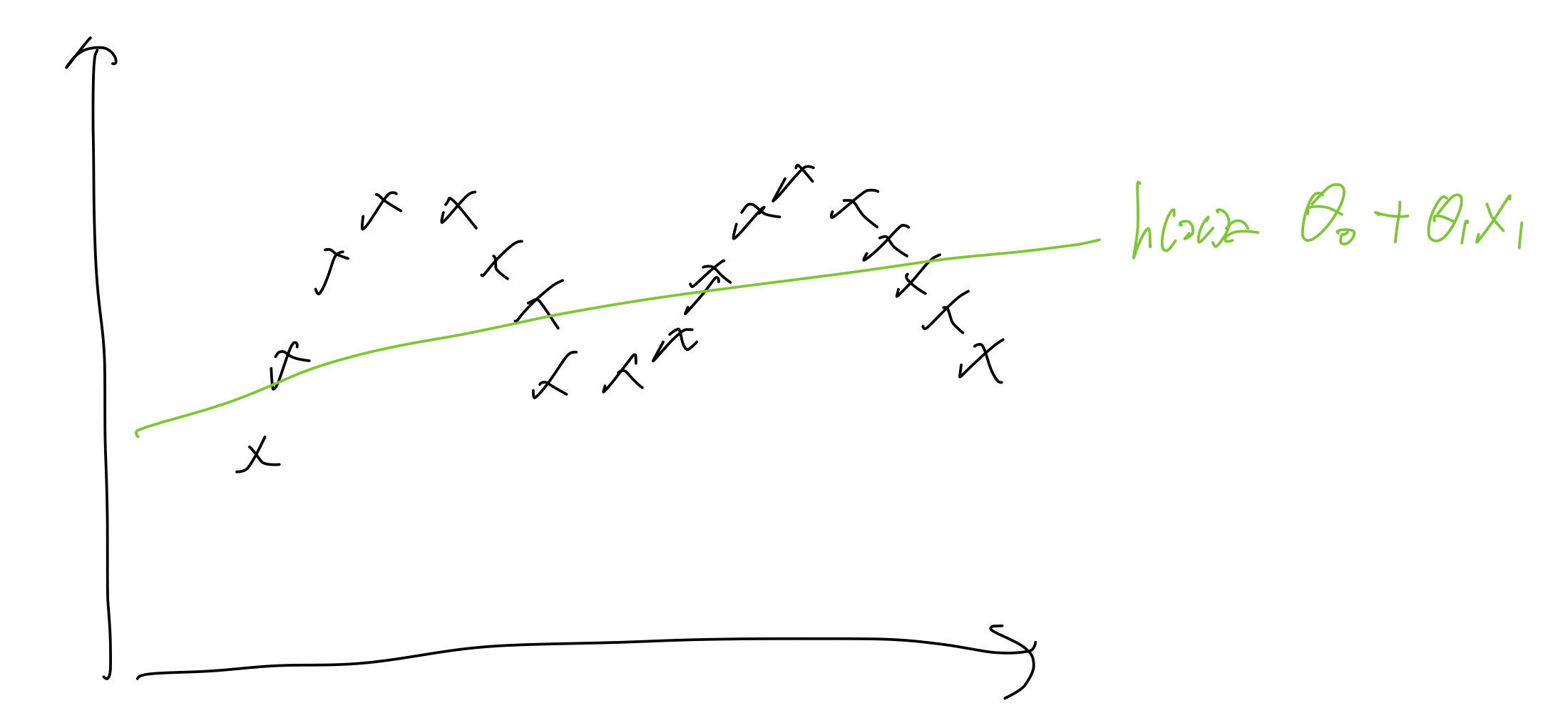
반면 locally weighted regression은 어떤 한 local 한 지역을 고려해서 선을 긋는다.

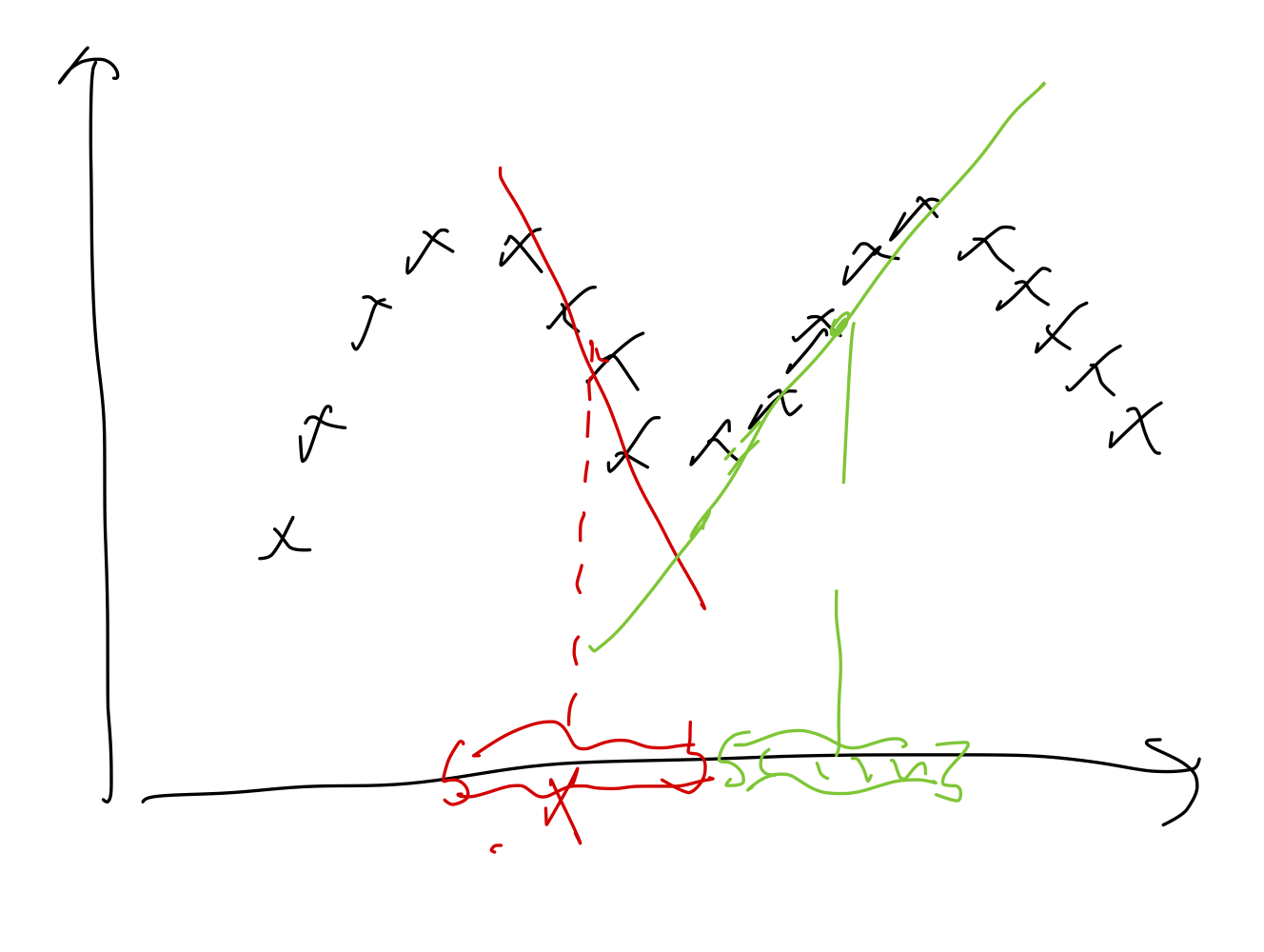
수식적으로 linear regression 과 어떤 차이가 있는지 살펴보자

Linear Regression :
to evaluate $h$ at contain $x$
Fit $\theta$ to minimize $\frac{1}{2}\sum_{i=1}^{n}{(h_\theta(x^i)-y^i)^2}$
return $\theta^\intercal x$

Locally weighted regression
Fit $\theta$ to minimize $\frac{1}{2}\sum_{i=1}^{n}{w^i(h_\theta(x^i)-y^i)^2}$
where $w^i$ is a "weight function"
$w^i=exp(\frac {-(x^i-x)^2}{2\tau^2})$

weight function을 잘 살펴보면, 각 샘플이 주어진 $x$와 가까울 수록, 가중치는 1에 가까워 지고, 멀어질 수록 가중치는 0에 가까워 지게 했음을 알 수 있다.

locally weighted regression 은 non-parametic algorithm이고 비모수적이다. 그러나 모수적인면이 전혀 없다고는 말할 수 없다. 가중치가 어떠한 분포를 따른다고 가정했기 때문이다.

$\tau$의 크기 는 가중치 함수의 width 를 결정한다. 즉 멀리 있는 데이터를 얼마나 더 고려할 지를 결정한다. $\tau$가 클 수록 멀리 있는 데이터를 가까이 있는 데이터와 동일하게 고려하고, $\tau$ 가 작을 수록 가까이있는 데이터를 고려한다.

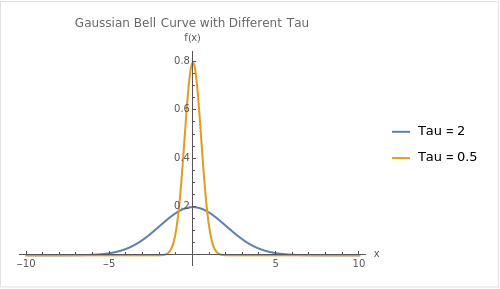
위 그래프는 tau 가 크고 작을 때의 gaussian bell curve이다. 보면 $\tau$가 작을 수록 가운데가 커진다.

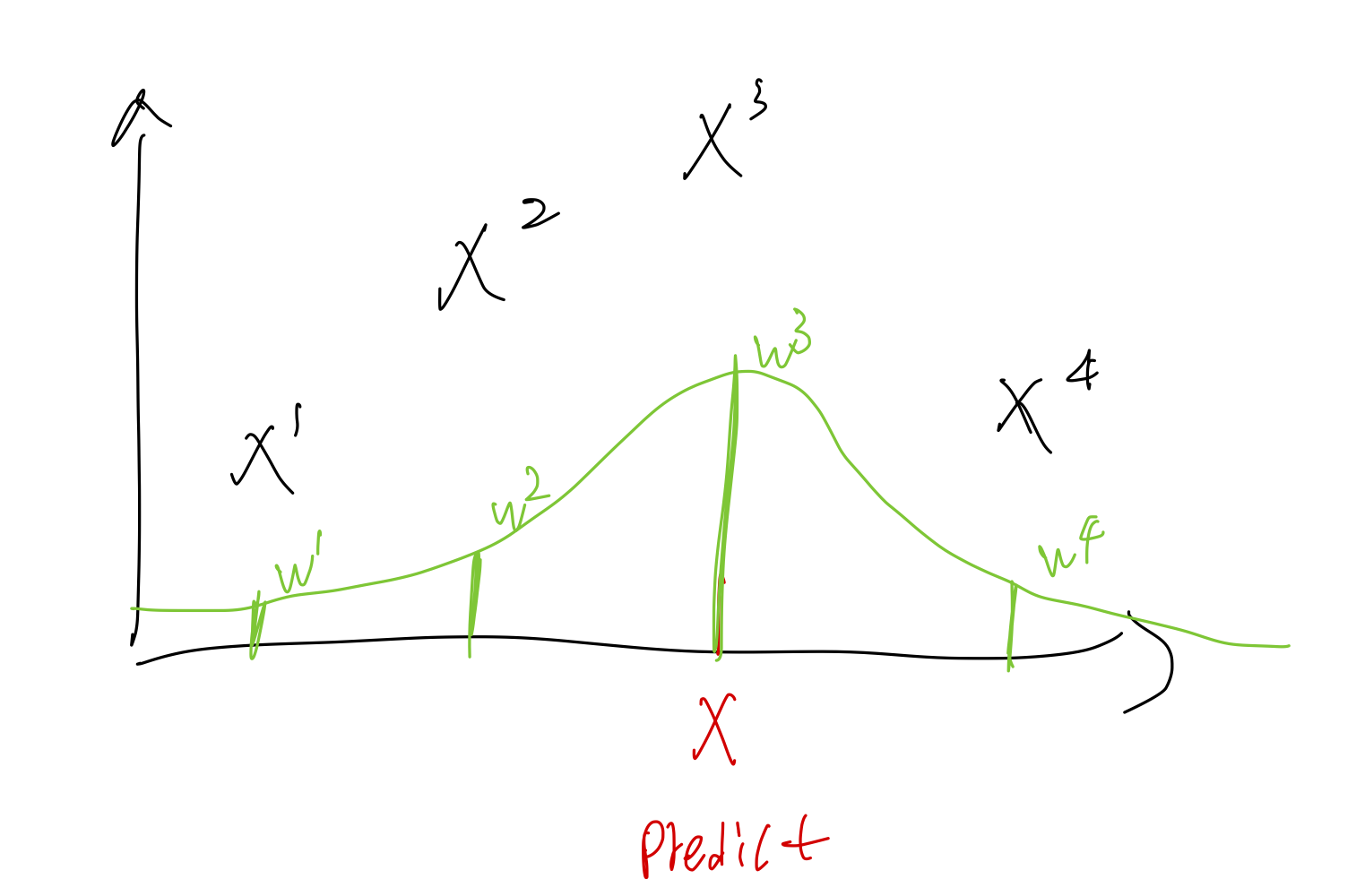
실제 데이터에 적용했을 때, X 를 predict 한다고 하면 그 오차에 대한 가중치를 얼마나 멀리 떨어져 있냐에 따라 다르게 준다. 그 가중치는 초록색 함수의 높이와 같다.

아래는 실제로 Data에 대해 locally weighted regression을 적용 했을 때의 plot이다.

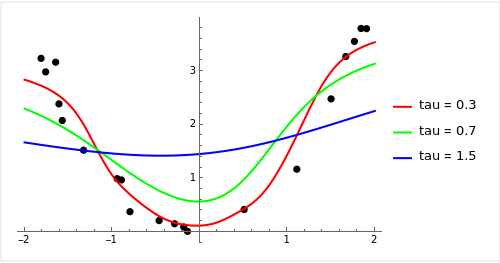
$\tau$가 작을수록 overfitting이 일어날 가능성이 커진다. 왜냐하면 가까이 있는 데이터만 고려하기 때문에 전체적인 경향을 파악하지 못하기 때문이다.
$\tau$가 크다면 반대로 underfitting이 일어날 수 있다. 너무 smooth 해져서 오히려 특징을 제대로 파악하지 못하게 된다.

$tau$가 작아질수록 wiggly해지고 클 수록 smooth 해진다.

gaussian bel lcurve 는 gaussian density 와 다르다. 후자는 적분해서 1이 되어야 한다.

실제로 가중치함수는 많은 모양들이 존재할 수 있다. 그러나 변수들이 독립적이라고 가정한다면, normal distribution을 사용하는 것이 합리적이다.

차원이 그렇게 많지 않고 data는 많이 존재할 때, locally weighted regression을 사용하면 좋은 결과가 나올 것이다.

Probabilistic interpretation

선형 회귀에 대한 확률론적 해석을 다루겠다. 왜 "하필" mean "square" error를 사용하는 지에 대해서도 이유를 알게 될 것이다.

우선 어떤 분포가 선형적이고 error를 가지고 있다고 가정하겠다. 그러면 다음과 같이 적을 수 있다.

$y^i = \theta^\intercal x^i+ \epsilon^i$
여기서 epsilon 은 어떤 오류를 나타낸다 unmodeled effects 혹은 random noise등으로 부를 수 있다. 집값을 선형적으로 예측한다고 한다면, 그날 판매자의 기분이나 날씨, 등등 여러 요소로 인해 랜덤하게 노이즈가 생기게 되는데 이러한 것을 나타낸다.

오류는 일반적으로 IID라고 가정한다. 실제세계에서 그렇지는 않지만 그렇게 가정하는 것이 수학적으로 깔끔하고 충분히 잘 작동하기 때문이다.

$\epsilon$이 IID 하다면, 우리는 이것을 gaussian distribution으로 나타낼 수 있다. 중심극한정리 때문이다. 이것에 대해서는 다루지 않겠다.

이것은 다음의미를 내포하고 있다.

동일하게 다음과 같이 적을 수 있다.

여담으로 여기서 $;$를 사용한 이유는 $\theta$는 랜덤변수가 아니기 때문이다. 어떤 random 한 event나 실험으로 인해 나오는 변수가 random variable인데 theta는 그렇지 않다.

위처럼 오류가 IID 하고 데이터의 분포가 선형적이다 라는 가정을 받아들인다면,

라고 적을 수 있다.

$L(\theta)$는 likelihood(우도)를 의미한다. 어떤 $\theta$가 있을 때 발생하는 확률과 같은 의미이다. 그러나 데이터가 변하지 않는 상태에서, $\theta$ 만 변화시킬 때 likelihood of theta 라는 용어를 사용한다.
반면, 데이터를 변경시킬 수 있을 때에는 $P(x):$ probability of data 라는 용어를 사용한다.

log likelihood

product 를 sum 으로 바꾸기 위해서 log를 취해보자

우리의 목적은 log likelihood를 최대화 하는 것이라고 말할 수 있다. 조금 더 첨언을 하자면, 우도는 데이터가 고정되어 있고, 분포가 변화할 때 데이터가 가지는 확률이라고 볼 수 있는데, 이 때 데이터들의 확률이 최대가 되도록 분포를 변화시키는 것이 우리의 목적이다. 그리고 이 분포가 $\theta$에 의해 변화되는 것이다.

즉 데이터들의 확률이 최대가 되도록 분포를 변화시키는 것이 우리의 목적이다.
그렇게 하기 위해서는 위 수식의 마지막 부분의 오른쪽을 최대화 시켜야 한다. 왼쪽항은 상수이기 때문이다.

$-$와 분산을 지우고 다음과 같이 나타낼 수 있다.

저번 시간에 배운 MSE가 그대로 나온다. 이제 우리는 MSE를 왜 사용하는가에 대한 질문에 답할 수 있다.

Q : 왜 MSE인가?

A : linear regression을 확률적으로 해석했을 때, error가 IID 하고 gaussian distribution을 따른다고 가정했을 때, log likelihood를 최대화 하는 것은 결과적으로 MSE를 최소화 하는 것과 같기 때문이다.

Logistic regression

이제 분류 문제에 적용해보자.
위에서 우리는 데이터의 분포에 대한 어떤 가정을 했고, 그에 맞춰 log likelihood를 최대화 하는 과정을 거쳐왔다.

분류문제도 이와 마찬가지로 진행할 것이다.

우선 분류 문제에 있어 linear regression을 사용하는 것은 안좋은 생각이다. 왜냐하면 linear regression은 outlier에 민감하게 반응하기 때문에 전체적인 패턴을 파악하는 것에는 한계가 있다.

또한 classification 문제에서는 output이 0또는 1인데, MSE에서는 값이 1보다 큰 경우가 있어 조금 이상한 점이 있다.

이러한 경우에 $x$값을 0과 1 사이로 mapping 시키는 활성함수를 사용할 수 있다. 대표적인 예시로 sigmoid function 이 있다. logistic function 이라고도 부른다.

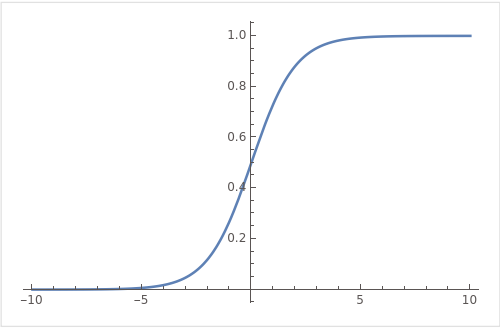
binary Classification 문제에서 $y$값은 0또는 1이다.
$P(y=1|x;\theta) = h_\theta(x)$라고 둔다면,
$P(y=0|x;\theta) = 1-h_\theta(x)$라고 둘 수 있다.

이 둘을 nifty 한 방법으로 하나의 방정식으로 만들 수 있다.

$P(y|x;\theta) = h_\theta(x)^{y}(1-h_\theta(x))^{1-y}$라고 둔다면, $y$ 가 1이거나 0일때 두가지 케이스를 하나로 압축시킬 수 있다.

이렇게 쓰고 위에 likelihood를 다시 계산해보자.

likelihood를 최대화 는 것이 우리의 목적이다.
이를 계산하기 위해 log likelihood로 바꿔보면,

Choose $\theta$ to maximize $l(\theta)$

이번 경우에 우리는 log likelihood를 maximize 해야한다. 이전에는 목적함수를 최소화 해야 했지만 이번에는 maximize해야 하므로 batch gradient ascent를 다음과 같이 적용할 수 있다.

기존에는 $-$ 였던 것이 $+$로 바뀐 점을 확인하자.

이 경우에 미분을 직접 수행하면 $\frac {\partial }{\partial \theta}l(\theta)$ 의 결과는 다음과 같다.

유도식은 아래에 적겠다.

$\begin{aligned} & \frac{\partial l(\theta)}{\partial \theta_j}=\frac{\partial}{\partial \theta_j} y \log \left(h_\theta(x)\right)+(1-y) \log \left(1-h_\theta\left(x_j\right)\right) \\ & =y \cdot \frac{\frac{\partial}{\partial \theta_j} h_\theta(x)}{h_\theta(x)}+(1-y) \frac{\frac{\partial}{\partial \theta_j} h_\theta(x)}{1-h_\theta(x)} \\ & \frac{\partial}{\partial \theta_j} h_\theta(x)=\frac{\partial}{\partial \theta_j} \frac{1}{1+e^{-\theta^{\top} x}}=\frac{\frac{\partial}{\partial \theta_j} e^{-\theta^{\top} x}}{\left(1+e^{-\theta^{\top} x}\right)^2}=\frac{x_j \cdot e^{-\theta^\intercal x}}{\left(1+e^{-\theta^{\top} x}\right)^2} \\ & =x_j h_\theta(x) \cdot\left(1-h_\theta(x)\right) \\ & \frac{\partial l(\theta)}{\partial \theta_j}=y\left(1-h_\theta\left(x_0\right) x_j+(y-1) h_\theta(x) x_j\right. \\ & =\left\{y-h_\theta(x)\} x_j\right. \end{aligned}$

Newton's Method

Gradient descent 는 좋은 방법이다. 그러나 많은 iteration이 필요하다.
데이터셋이 그렇게 크지 않을 때는 Newton's method가 좋은 방법이 될 수 있다. 이 방법은 expensive 하지만 대부분의 상황에서 10번 이내의 반복으로 문제를 해결할 수 있다.

Newton's method 는 $f(\theta)=0$ 을 만족시키는 $\theta$를 찾기위한 방법이다.

위의 경우에서 우리는 log likelihood를 maximize 시키고 싶었다. 그렇게 하기 위해서는 likelihood 의 미분값이 0이되는 지점을 찾으면 된다.

즉 $l'(\theta) = 0$ 인 지점을 찾으면 된다. log likelihood 는 concave 하므로 이렇게 해도 괜찮다.

likelihood 의 도함수에 newton's method를 적용하는 방식으로 likelihood의 최댓값을 찾을 수 있다.

어떤 $f(\theta)$에 대하여 뉴턴의 방법을 적용시키면

이렇게 적을 수 있다. 여기서 $f(\theta)=l'(\theta)$ 라고 가정한다면,

라고 적을 수 있다.

quadratic convergence

뉴턴의 방법은 이차함수적으로 수렴하는데, 이는 최솟값에 가까워질 수록 원래 오류가 0.01 이였다면 -> 0.0001 -> 0.00000001 식으로 점점 오류가 줄어드는 것을 의미한다.

Vector form of newton's method

newton's method를 vecotr form 으로 표현하게 되면 다음과 같이 된다.

$\theta \in R^{n+1}$ 일 때 $\nabla_\theta l \in R^{n+1}$ 이다.
그리고 $H$는 헤시안을 의미하는데, $H\in R^{(n+1)\cdot(n+1)}$ 이다.

헤시안의 역함수를 구해야 하는데, 데이터의 차원이 10000, 100000단위로 가게 되면 사실상 역함수를 구하기는 불가능하다.

차원이 적은 경우에는 사용하기 좋다.

끝