CS229 | Lecture 4 Perceptron & Generalized Linear Model

HAIM BIN·2023년 7월 11일

cs229

Stanford CS229: Machine Learning

목록 보기

5/8

Outline

Perceptron
Exponential Family
Generalized Linear Models
Softmax Rogression(Multiclass Classification)

Perceptron

퍼셉트론은 60년대 나온 이진분류 알고리즘이다. 상당히 단순한 구조를 가지고 있다.

이전에 배웠던 sigmoid와 같이 비교해보자

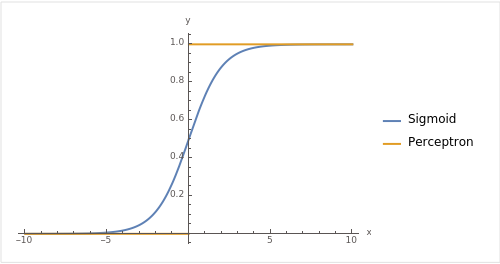
위 그림에서도 볼 수 있듯이 Perceptron은 Sigmoid의 하드한 버전이라고 볼 수 있다. x가 0보다 작으면 0 0보다 크면 1인 단순한 구조를 가진다.

g(x) = \begin{cases} 1 & \text{if } x \geq 0 \\ 0 & \text{if } x < 0 \end{cases}

이것의 hypothesis funtion은 다음과 같이 작성할 수 있다.

h_\theta(x) = g(\theta^\intercal x)

Perceptron에서 사용하는알고리즘은 다음과 같이 간단하다.

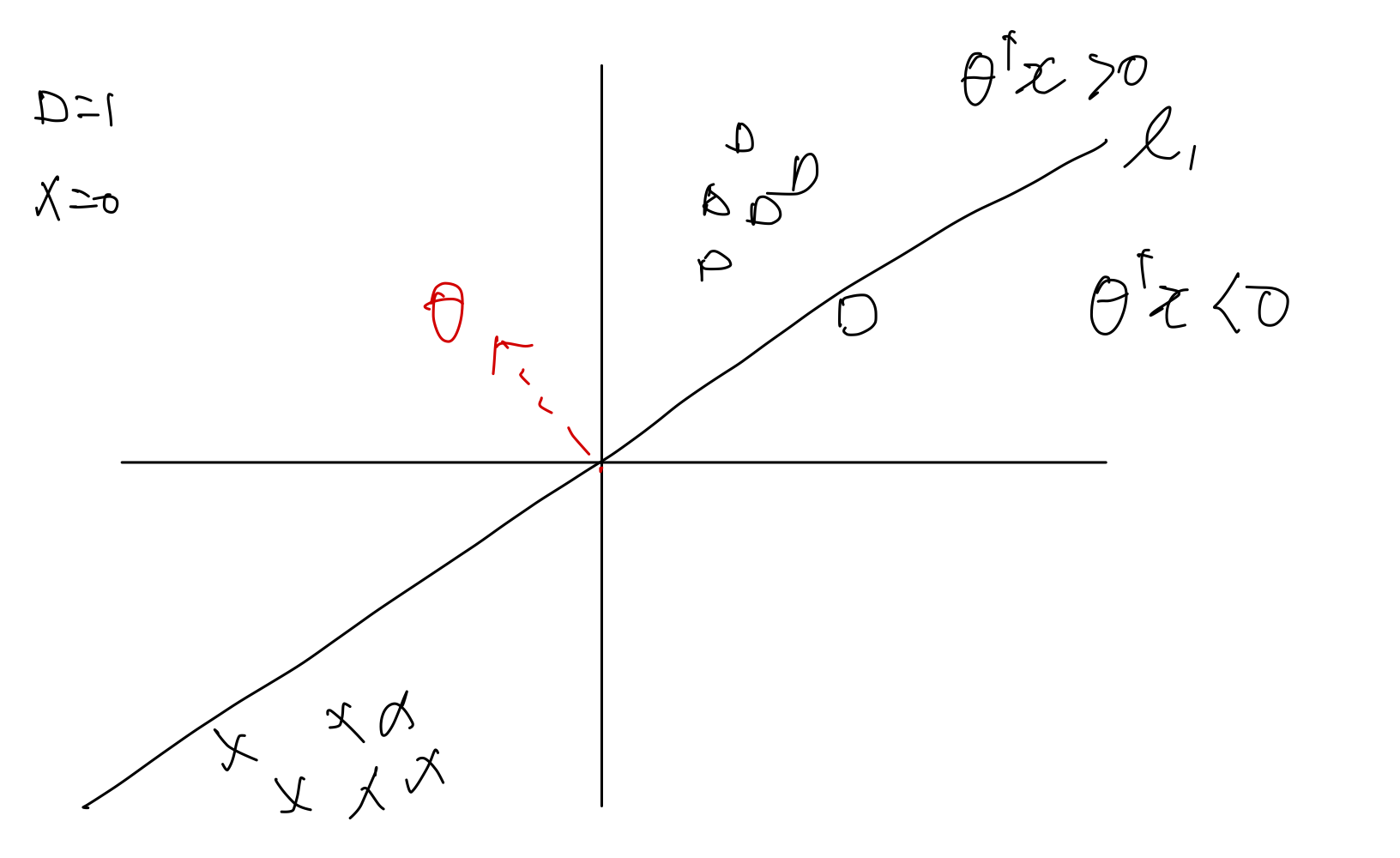
\theta_j := \theta_j + \alpha(y^i-h_\theta(x)^i)x_j^i

다음과 같이 두 샘플을 분류하고 있는 boundary line $l_1$ 이 있다고 가정했을 때, 1사분면에서 네모 하나가 잘못 분류되어 있음을 확인할 수 있다.

이 과정에서 업데이트를 해보자.

먼저 잘 분류되어 있는 것들에 대해서 파라미터는 업데이트를 진행하지 않는다.
$y^i-h_\theta(x)$ 가 0이되어 버리기 때문이다.

만약 잘 분류되어 있지 않다면 두 가지 경우로 나눠볼 수 있다.

Case1: 실제 ( $y^i$ ) 는 1인데 분류( $h_\theta(x)$ )는 0인 경우
$y^i-h_\theta(x)=1$
$\theta_j := \theta_j + \alpha x_j^i$
Case2: 실제 ( $y^i$ ) 는 0인데 분류( $h_\theta(x)$ )는 1인 경우
$y^i-h_\theta(x)=-1$
$\theta_j := \theta_j - \alpha x_j^i$

위의 그림은 실제는 1인데 분류는 0으로 되어있으므로 Case1에 해당한다.
위의 업데이트가 의미하는 바는 $\theta_j$ 에 $x_j^i$ 의 성분을 추가하는 것으로 이해할 수 있다.

반대로 Case2의 경우는 - 이므로, $\theta_j$ 에 $x_j^i$ 의 성분을 빼는 것으로 이해할 수 있다.

그림으로 다음과 같이 생각해볼 수 있다.

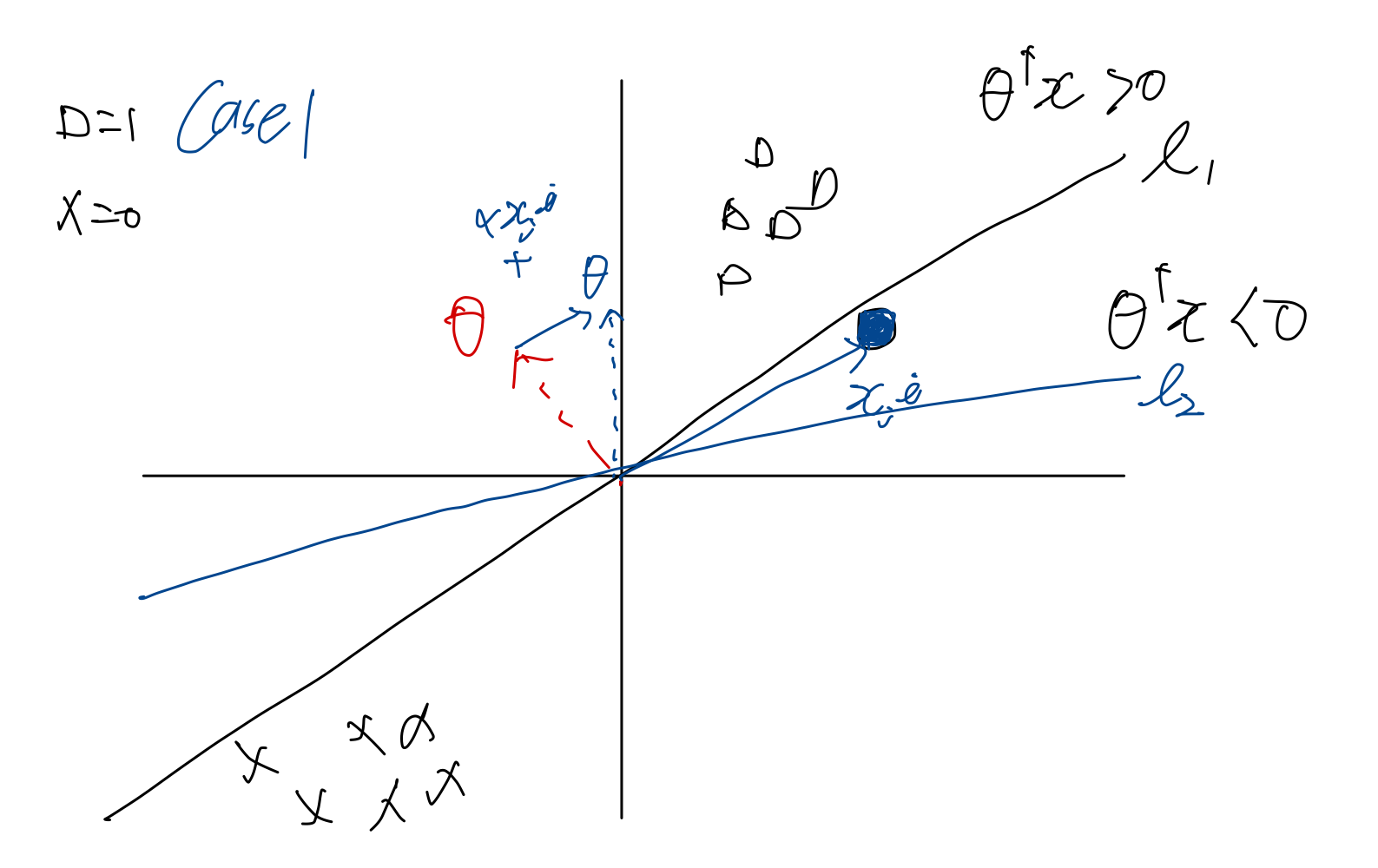
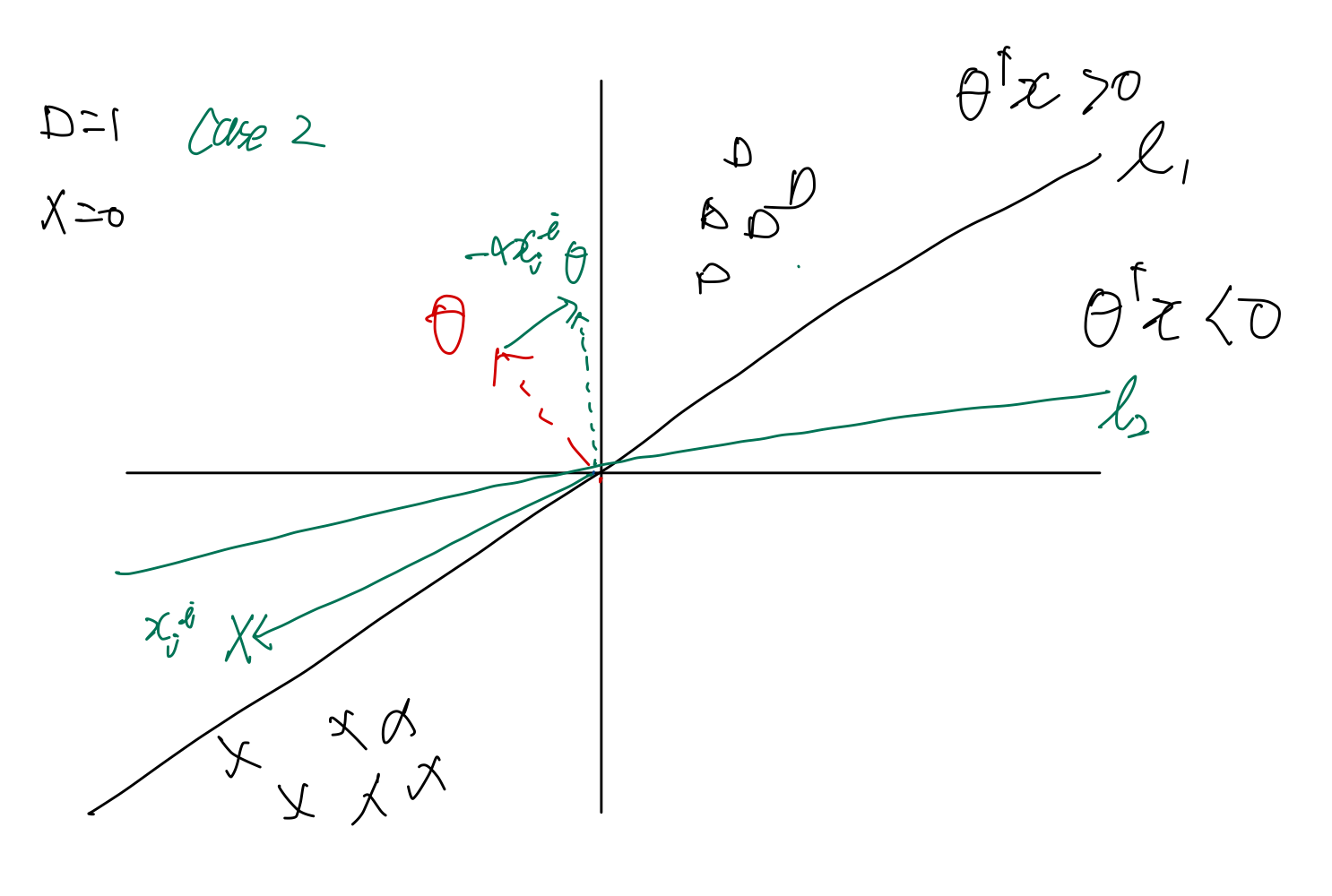
두 케이스 모두 $\theta$ 가 비슷한 방향으로 정리됨을 알 수 있다.

퍼셉트론은 간단하고 이해하기 쉽지만 실제로는 쓰이지 않는다. 왜냐하면 확률론적인 해석을 할 수 없기 때문이다. 또한 xor 문제와 같은 것도 풀지 못한다..

Exponential Family

어떤 PDF(Probability Density Function)를 다음과 같이 적을 수 있다. (PMF 도 가능하다)

$P(y;\eta) = b(y)exp(\eta^\intercal T(y)-a(\eta)) = \frac {b(y)exp(\eta^\intercal T(y))} {e^{a(\eta)}}$

용어를 정리하겠다.

$y$ : 우리가 가지고 있는 데이터를 의미한다.
$\eta$ : natural parameter -> 데이터의 distribution을 결정하는 상수
$T(y)$ : sufficient stastic -> 모분포를 추정하는데 필요한 모든 정보가 들어 있는 통계량을 충분 통계량이라고 부른다. 여기서는 $y$ 이다.
(조금 더 덧붙여 설명하자면, 베르누이 시행의 경우에는 1이 언제나왔는 지 알면 0은 자동으로 따라서 나오므로 1이라는 결과에 대한 통계값만 있으면 0은 자동으로 나온다. 이러한 경우에 충분 통계량은 1 또는 0의 통계값일 것이다.)
$b(y)$ : Base measure -> 분포가 적절히 scaled 되도록 하는 normalization term 이다.
$a(\eta)$ : log - partition -> log 형태로 표현된 normalization factore 이다.

이 용어들에 대한 엄밀한 이해는 현재 단계에서는 중요하지 않다. 그리고 현재는 모든 $\eta$ 가 스칼라라고 가정하겠다. 벡터면 그에 맞게 변환시키기만 하면 되는데 여기서 다루지는 않겠다.

어떤 분포가 Exponential family에 있다고 가정한다면, 그 family의 특징을 모두 가지고 있다고 말할 수 있다.

흔히 알고 있는 베르누이 분포 또한 Exponential family의 한 종류이다.
우리가 알고있는 형식을 마사지 해서 Exponential family의 형태로 바꿔보면 된다.

Bernoulli distribution to Exponential family

Bernoulli
$\phi$ = probabiliy of event
$P(y;\phi) = \phi^y(1-\phi)^{(1-y)}$
$= exp(log(\phi^y(1-\phi)^{(1-y)}))$
$=exp[log(\phi/(1-\phi))y + log(1-\phi)]$

위 분포를 Exponential family의 각 함수와 상수에 대응시킬 수 있다.

$b(y) = 1$
$T(y) = y$
$\eta = log(\frac {\phi}{1-\phi}) => \phi = \frac {1}{1+e^{-n}}$
$a(\eta) = -log(1-\phi) => -log(1-\frac {1}{1+e^{-\eta}}) = log(1+e^\eta)$

이렇게 대응시킬 수 있으므로 베르누이 함수는 Exponential family 의 한 종류라고 볼 수 있다.

잘 보면 $\phi$ 가 sigmoid 함수 형태인 것을 알 수 있다. (이것은 우연이 아니다!!)

Gaussian distribution to Exponential family

Gaussian distribution도 생각해보자 이 분산은 평균과 분산이라는 변수를 가지고 있다. 여기서는 고정된 분산을 생각해보자.

Gaussian Distribution
Assume $\sigma^2$ = 1
$P(y;\mu) = \frac {1}{\sqrt{2\pi}}exp(-\frac{(y-\mu)^2} {2}$ )
$= \frac {1}{\sqrt{2\pi}}e^{\frac {-y^2} {2}}exp(\mu y-\frac {1} {2} \mu^2)$

위 형태를 Exponential family의 각 함수와 상수에 대응시킬 수 있다. 베르누이에서 $\phi$ 였던 것이 가우시안 분포에서는 $\mu$ 로 바뀌었다. 우리가 가정하고 있는 어떤 Canonical parameter를 $\eta$ (natural parameter)로 바꾸는 과정임을 알 수 있다.

일단 Exponential family의 형태로 바꿀 수 있다면, 그 분포는 그 famework 안에서 이해할 수 있다.

위 가우시안 분포도 Exponential family의 형태로 마사지 해보자.

$b(y) = \frac {1}{\sqrt{2\pi}}$
$T(y) = y$
$\eta = \mu$
$a(\eta) = \frac {\mu^2}{2} = \frac {\eta^2}{2}$

이렇게 대응시킬 수 있으니 가우시안 분포도 Exponential family의 구성원임을 알 수 있다.

Properties of Exponential family

우리가 Expoenential Family를 사용하는 이유는 이것이 좋은 수학적 속성을 가지고 있기 때문이다.

다음과 같은 특징들을 사용한다.

MLE is concave

NLL is convex

$E[y;\eta] = \frac {\partial}{\partial\eta}a(\eta)$

$\sigma[y;\eta] = \frac {\partial^2}{\partial\eta^2}a(\eta)$

일반적으로 평균이나 분산을 구하기 위해서는 적분을 해야한다. 하지만 Exponential family의 경우에는 미분을 하면 평균과 분산이 나온다.

Member of Exponential family

Real - Gaussian
Binary - Bernoulli
Count(non-negative integer) - Poisson
Positive Real - Gamma, Exponential
Distn - Beta,Dirichlet, Bayesian ( 확률 분포에 대한 확률 분포)

표현하고자 하는 데이터의 종류에 따라 위와 같은 확률분포를 잘 선택해서 사용할 수 있다.

GLM

General Linear model
GLM exponential 에선는 y 값 output을 다루고 있다.

exponential family 에서 적절한 구성원을 구하고 모델에 연결시킬 수 있다.

Assumption / Design choice

$y|x;\theta$ ~ Exponential Family $(\eta)$
: y의 분포가 exponential family 라고 가정한다.

$\eta = \theta^\intercal x$ , $\theta \in \R^n,x \in \R^n$
: $\eta$ 가 선형적이고 $\theta$ 와 $x$ 가 차원이 같다.

Test Time : Output $E[y|x;\theta]$
: Mean $h_\theta(x) = E[y|x;\theta]$ 어떤 x 에 대한 y 의 기댓값은 우리의 예측값이 된다는 뜻이다. 본질적으로 가설함수가 x 에 대한 y 의 기댓값이라는 것을 나타낸다.

Bernoulli를 사용하든, Gaussian을 사용하든 그것이 Exponential Family 라면 GLM 안에서 해석할 수 있고 동일한 가설함수 $E[y|x;\theta]$ 를 가진다고 할 수 있다.

Visualize 해보자

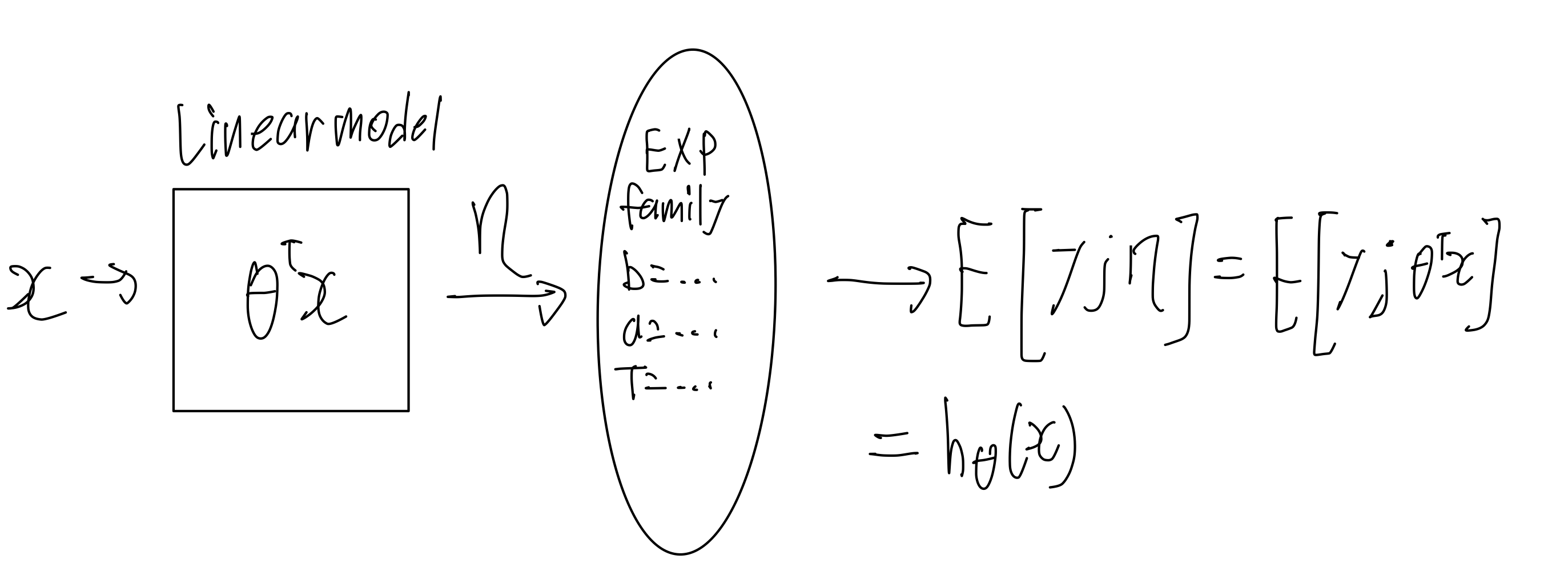
$x$ 를 통해 $\theta$ 를 gradient descent를 사용해 훈련한다. 그 훈련의 결과가 exponential family distribution 의 상수가 된다. 그리고 그 분포의 평균이 예측 결과이자 우리가 만들고자 하는 가설이 된다.

훈련 시간에 하는 일은 likelihood를 최대화 하는 일이다. 조금 더 풀어서 설명하자면, 주어진 데이터가 있을 때 이것이 가장 잘 일어날 수 있도록 $\theta$ 를 조정하는 것이다. 이것이 MSE를 최소화 하는 것과 같음을 이전시간에 배웠다. 훈련시간에 likelihood를 최대화 했다면, 그 훈련의 결과 값은 Exponential family의 parameter를 결정하기 위해 사용된다. 그리고 우리가 실제로 예측(Test time)을 할 때는, 그 분포의 기댓값으로 예측을 한다.

우리가 MSE를 사용해 최적화를 진행했을 때 얻는 것은 그 데이터들의 평균을 나타내는 하나의 직선이다. 그 직선은 어떻게 나왔는가? 데이터들이 가우시안 분포를 따른다고 가정 했기 때문에 나올 수 있었다. 그리고 가우시안 분포는 Exponential family 이다. 우리는 gradient descent를 통해 $\theta$ 를 구했고 그것은 어떤 가우시안 분포로써 나타난다. 그 가우시안 분포의 평균이 우리가 구하려고 하는 가설이고 그 가설이 직선이다.

GLM Training

모든 GLM은 다음의 Learning Update Rule을 따른다(stochastic 인 경우)

$\theta_j := \theta_j + \alpha(y^i-h_\theta(x^i))x_j^i$

용어들을 정리하겠다.

$\eta$ - natural parameter
$\mu = E[y;\eta] = g(\eta)$ -> Canonical Response function
$\eta = g^{-1}(\mu)$ -> canonical link function
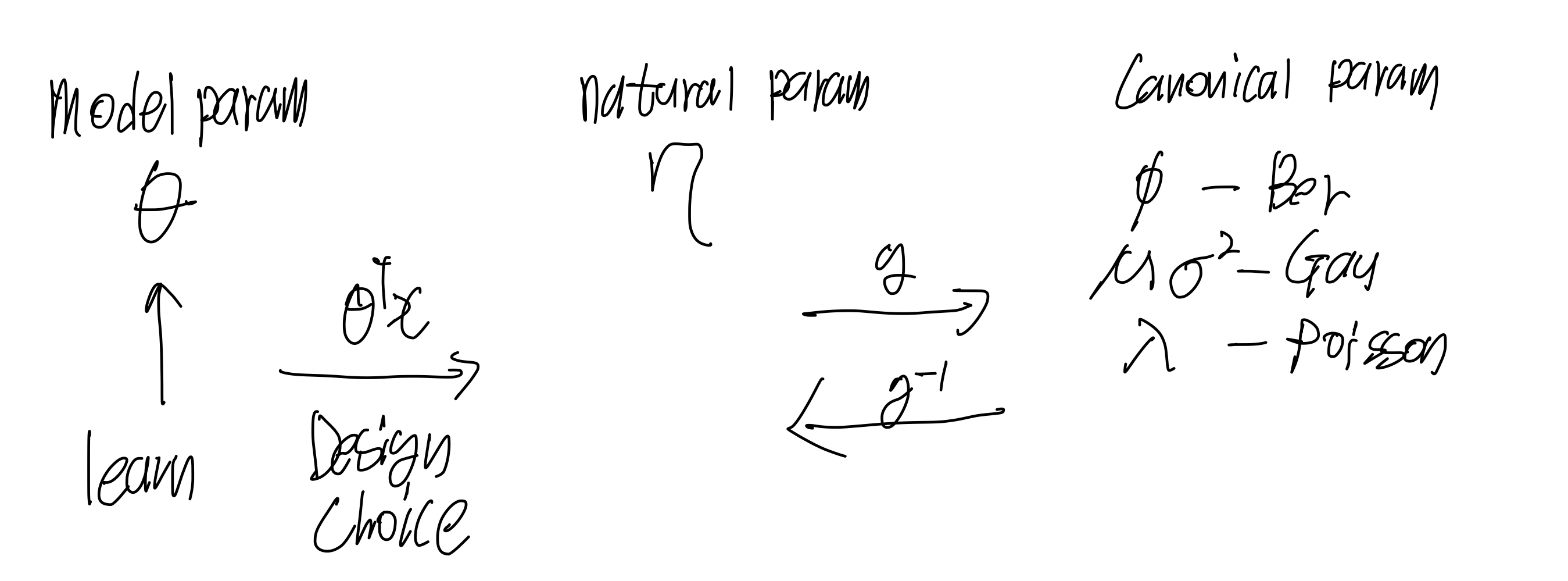
$g(\eta)=\frac {\partial}{\partial \eta}a(\eta)$ $\ \ \because \frac {\partial}{\partial \eta}a(\eta) = \mu$

model parameter $\theta$ 는 우리가 학습시키는 parameter이다.
그리고 우리는 학습시킨 model parameter 를 natural parameter 로 선형 적으로 재 매개변수화 하기로 했다.

$\eta$ 를 선형 모델로 재매개변수화 하기로 하는 것과 같은 것을 Design Choice 라고 한다.

natural parameter와 canonical param 사이는 $g$ 로 연결이 되어있다 우리가 원하는 목적에 따라 대수적인 작업을 거치고 나면, 원하는 분포를 만들어 낼 수 있다.

Logistic Regression을 예로 들어보자. 처음에 대수적으로 이를 설명할 때는 sigmoid function을 그냥 음 이게 좋을것 같아 하고 하늘에서 뚝 떨어져서 사용했지만 이제 우리는 이걸 왜 사용하는 지 해석할 수 있다.

binary regression 문제에서 분포가 exponential family 중 하나인 bernoulli를 따른다고 가정했을 때

h_\theta(x) = E[y|x;\theta]=\phi = \frac {1}{1+e^{-n}} = \frac {1}{1+e^{-\theta^\intercal x}}

와 같이 가설이 나온다.

bernoulli 를 exponential family로 대응시킬 때 canonical parameter 와 log - partition이 다음과 같이 만들어 졌다.
$\eta = log(\frac {\phi}{1-\phi}) => \phi = \frac {1}{1+e^{-n}}$
$a(\eta) = -log(1-\phi) => -log(1-\frac {1}{1+e^{-\eta}}) = log(1+e^\eta)$

여기서 log -partition을 미분하면 $\frac {e^\eta}{1+e^\eta}$ 이 만들어진다. 그리고 exponential family의 특성중에서 log - partition을 미분하면 평균이 나옴을 알고 있다.
위 아래를 $e^\eta$ 로 나누면 $\frac {1}{1+e^\eta} = \phi$ 가 된다! 즉 베르누이 분포의 평균은 canonical 상수 그 자체이다. 대수적으로 생각하면 당연하긴 하지만 exponential family의 관점에서 이렇게 볼 수도 있다.

아무튼 중요한 것은 sigmoid function의 모양이 그냥 나온 것이 아니라는 것이다. 모델의 결과값을 sigmoid function에 집어넣는 것은 $\eta$ 를 $\phi$ 로 변환하는 과정으로 이해할 수 있다. 변환하는 과정에서 베르누이라고 가정했기 때문에, 그런 모양이 나온 것이다.

Regression

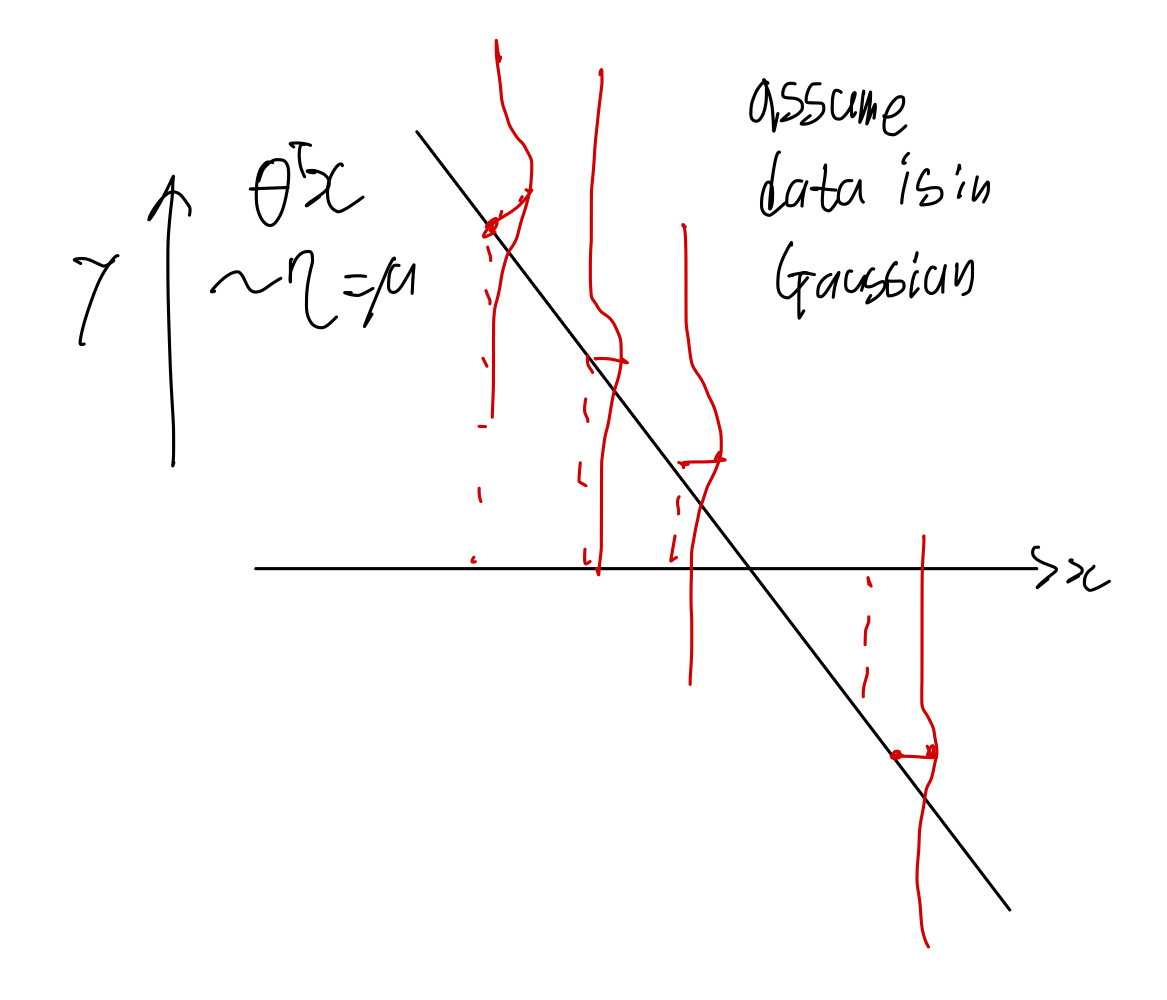
시각화 하면 다음과 같다, 모든 $x$ 에 대하여 $y$ 값이 gaussian distribution을 가진다고 가정한다.

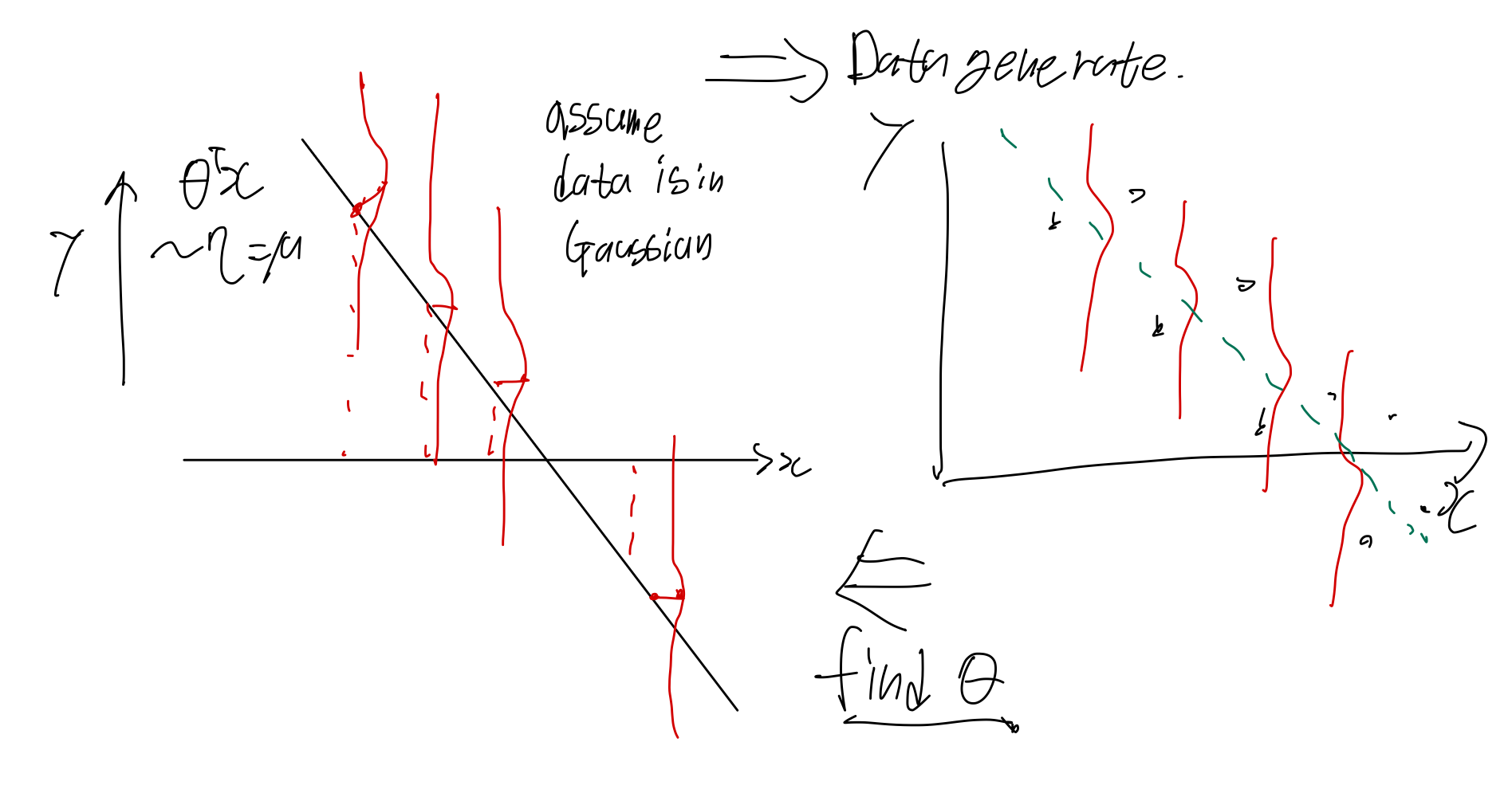
우리가 실제로 보는 데이터는 샘플링된 데이터이다. 우리는 이 데이터들이 이전 그림에서 만들어진 데이터들이라고 가정하고 문제를 푸는 것이다.

경사하강법과 데이터들을 통해 likelihood를 최대화 하는 $\theta$ 를 찾는다. (MSE를 최소화) 우리가 처음에 가우시안 분포라고 가정했기 때문에 $\eta$ 를 $\theta^\intercal x$ 라고 쓸 수 있다. 그리고 이 값은 exponential family의 성질에 의해 (log -partition의 미분이 평균) canonical parameter 인 $\mu$ 와 같다.

Classification

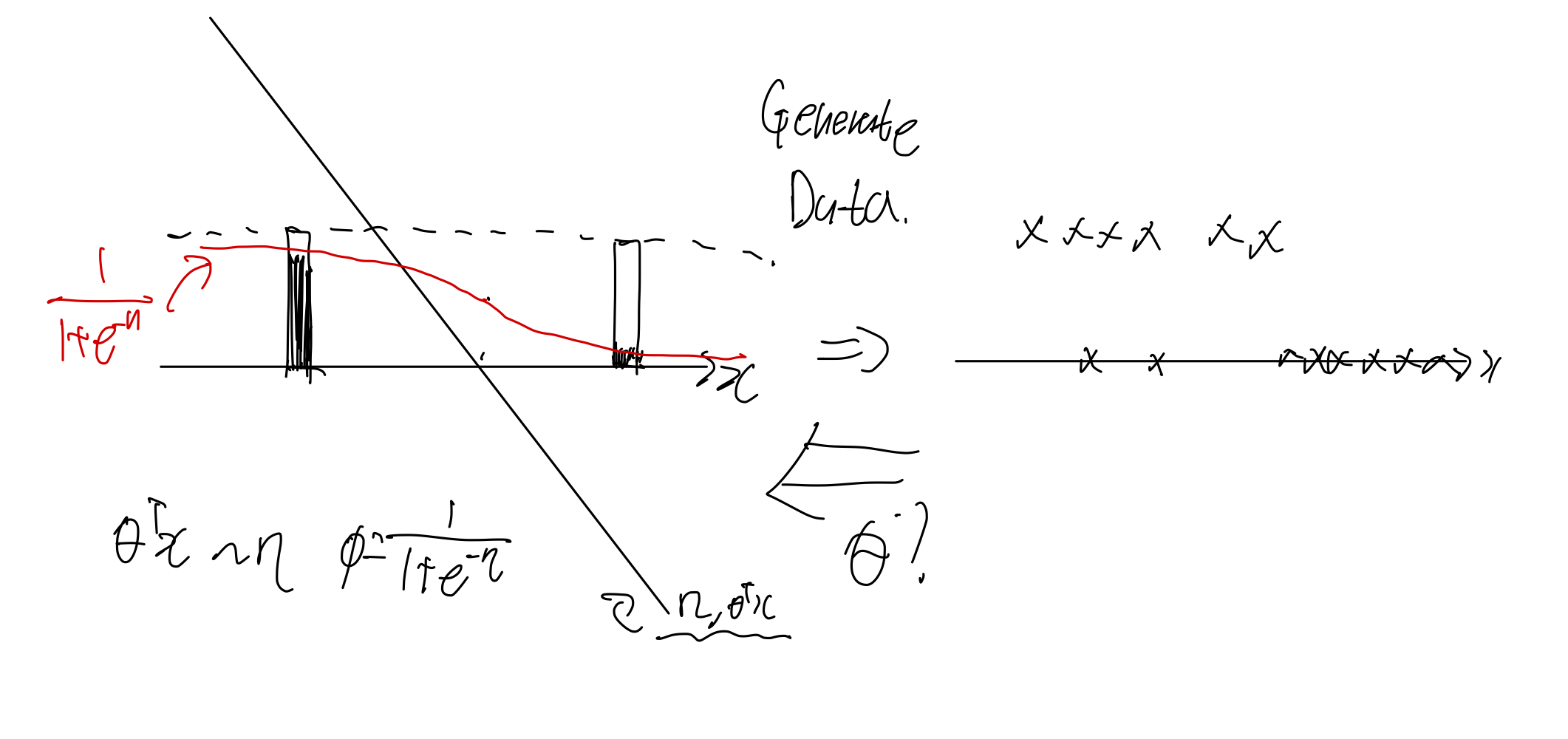
이진 분류 문제에서는 일반적으로 데이터가 베르누이 분포를 가지고 있다고 가정한다. 이때 어떤 정해진 $\phi$ 가 있고 거기로부터 sample 들이 만들어진다고 가정해보자.

똑같이 likelihood를 최소화 하는 $\theta$ 를 찾는다. 그러나 이번에는 $\theta^\intercal x$ 를 예측하는데 바로 사용하지 않고 sigmoid function을 통과시킨다. 왜냐하면 GLM 에서 우리는 평균을 사용해서 예측하기로 약속했었다. 베르누이 분포의 평균은 $\phi$ 그 자체이다.
그리고 이 $\phi$ 는 $\frac {1}{1+e^{-\eta}}$ 이다.

Remind:
Train time : find right $\theta$
Test time : output $E[y|x;\theta]$

Softmax regression

이제 다중 클래스 분류에 대해 이야기 해보자.

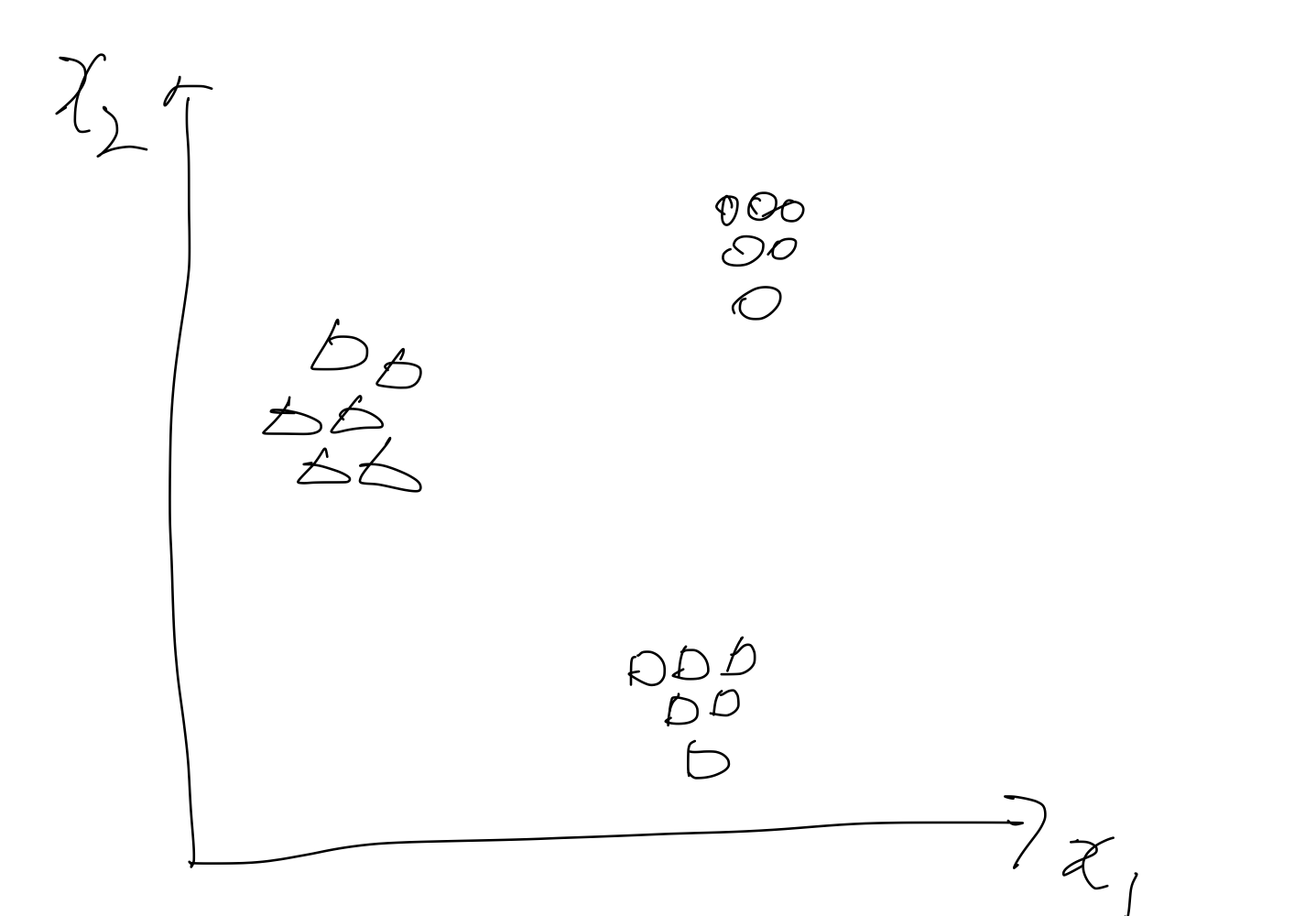
위와 같은 데이터 분포가 있다고 했을 때
이들을 어떻게 분류할 수 있을 까?
먼저 몇 가지를 정의하겠다.

$x^i \in \R^n$
$k =$ #classes
Label $y = \{\{0,1\}^k\}$ e.g {0,0,1}
이런 표현을 one hot code라고 부른다. 정해진 클래스에 해당하는 위치만 1이고 나머지는 0이다.
$\theta_{class} \in \R^n$

각각의 클래스마다 $\theta$ 를 다르게 설정한다고 생각하면 된다.

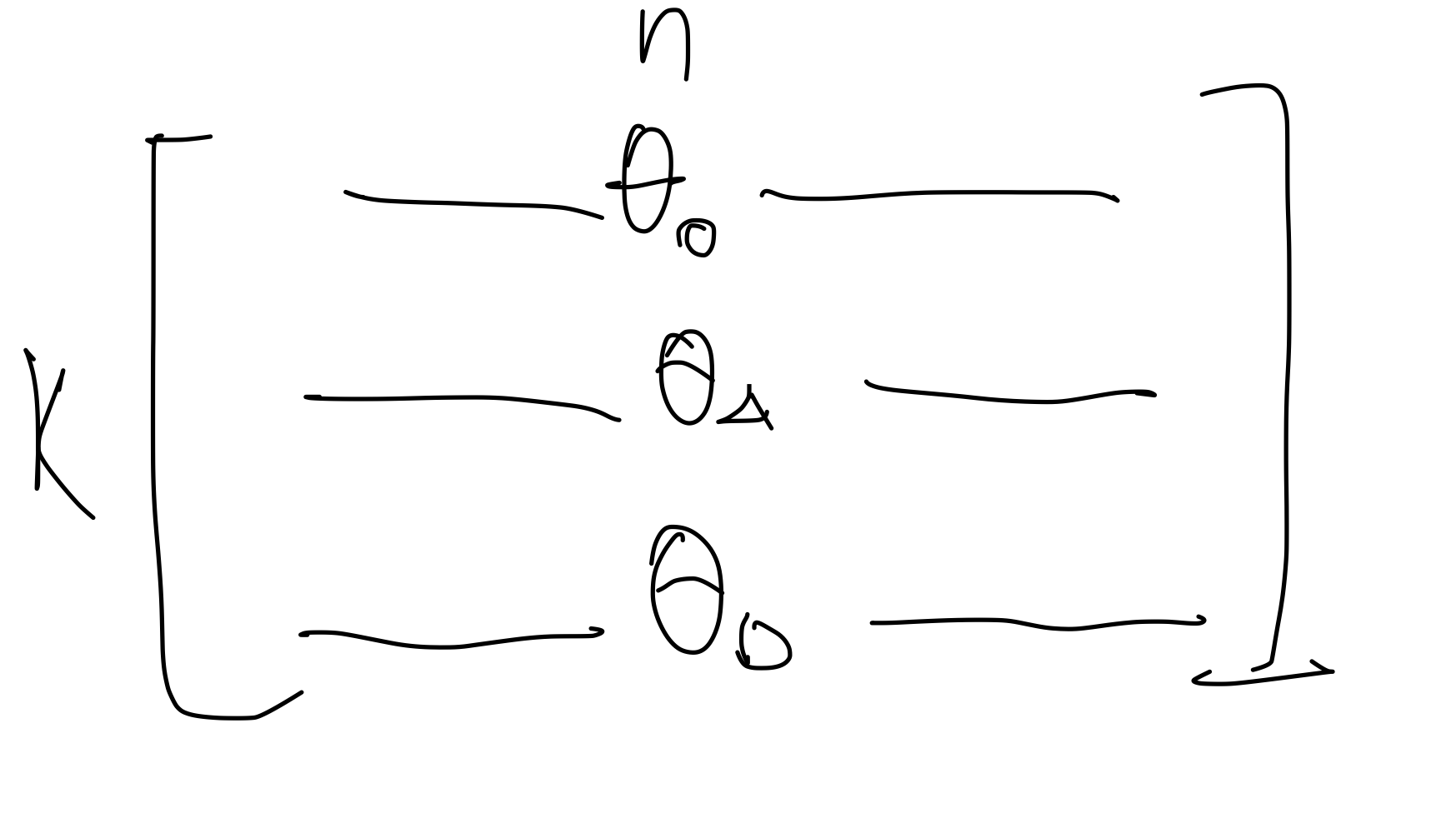
parameter를 이런 식으로 표현 가능하다.

기본적으로 수행하는 방식은 이전과 같다.

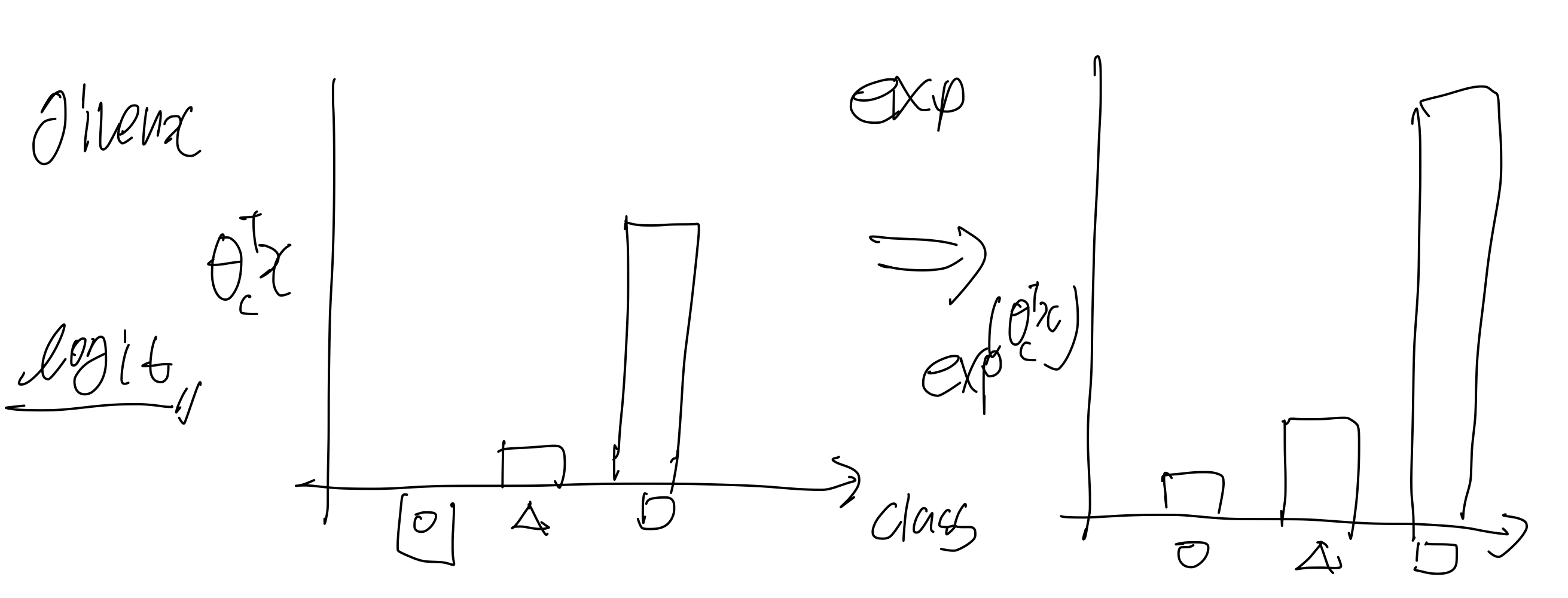
각각의 클래스에 대한 $\theta_c^\intercal x$ 가 있을 텐데, 그 raw 값을 logit 이라고 한다. 여기서 우리는 각 클래스의 확률 분포를 원하므로 이 값을 잘 조절해서 확률적으로 바꿔줘야 한다. 그러기 위해서는 먼저 exp를 해줘 양수로 바꿔준 다음에 Normalize를 수행해주면 된다.

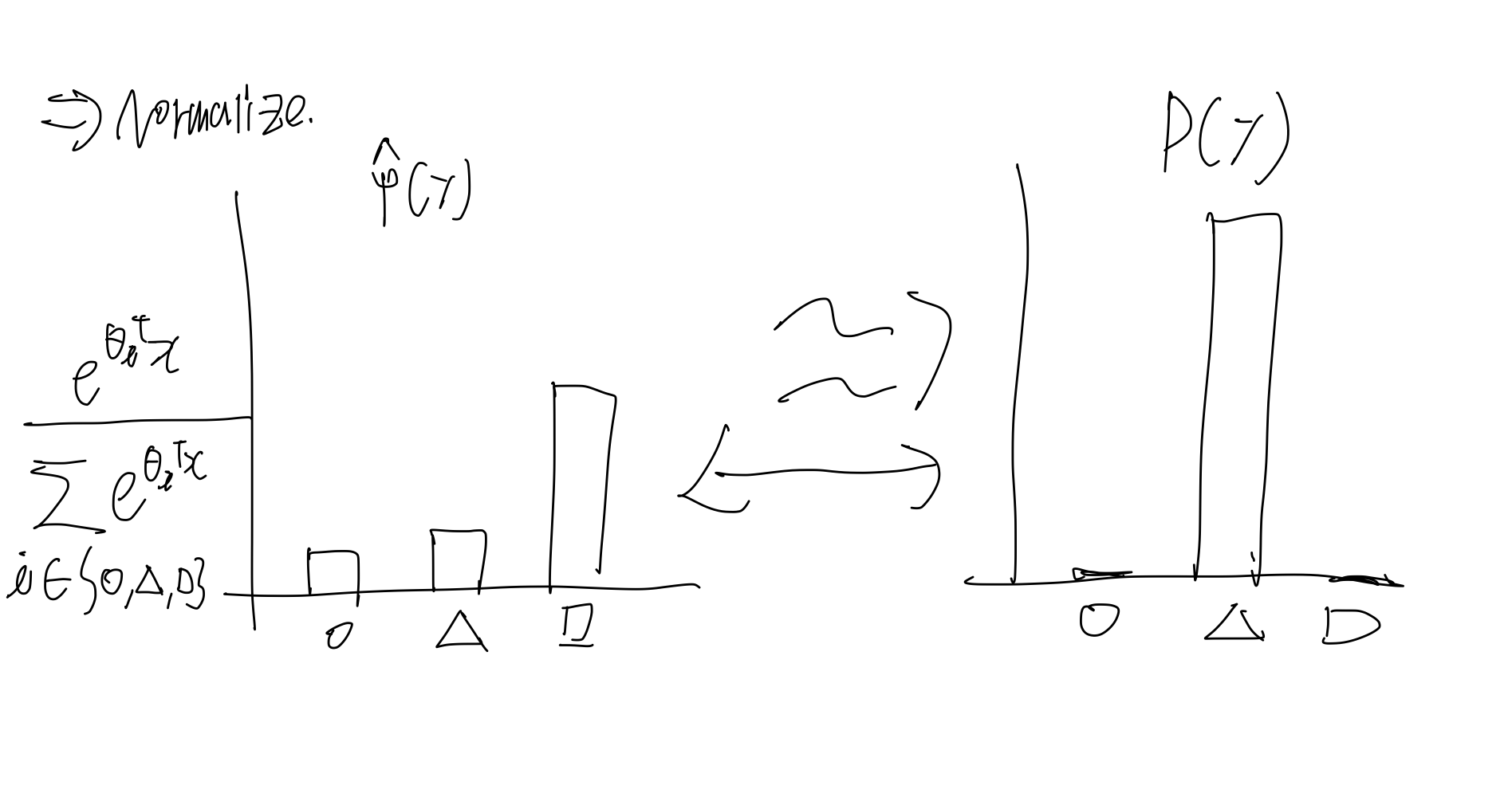
Normalize를 취하면 왼쪽 그림과 같이 된다. 그리고 만약 실제 target이 오른쪽 그림과 같다면, 우리는 왼쪽의 그림이 오른쪽 처럼 되기를 원할 것이다. 그렇게 하기 위해서는 $\theta$ 를 업데이트 해야 하고 이를 위해 CrossEntropy라는 것을 사용한다.