Outline

• Generalized Discriminant Analysis
• Generative Vs Discriminative Comparision
• Naive Bayes
• Laplace smoothing
• Event models

Gaussian Discriminant Analysis (GDA)

변수가 여러개인 경우에 Discriminant를 사용하는 경우를 살펴보자.
다음과 같이 Assume을 할 수 있다

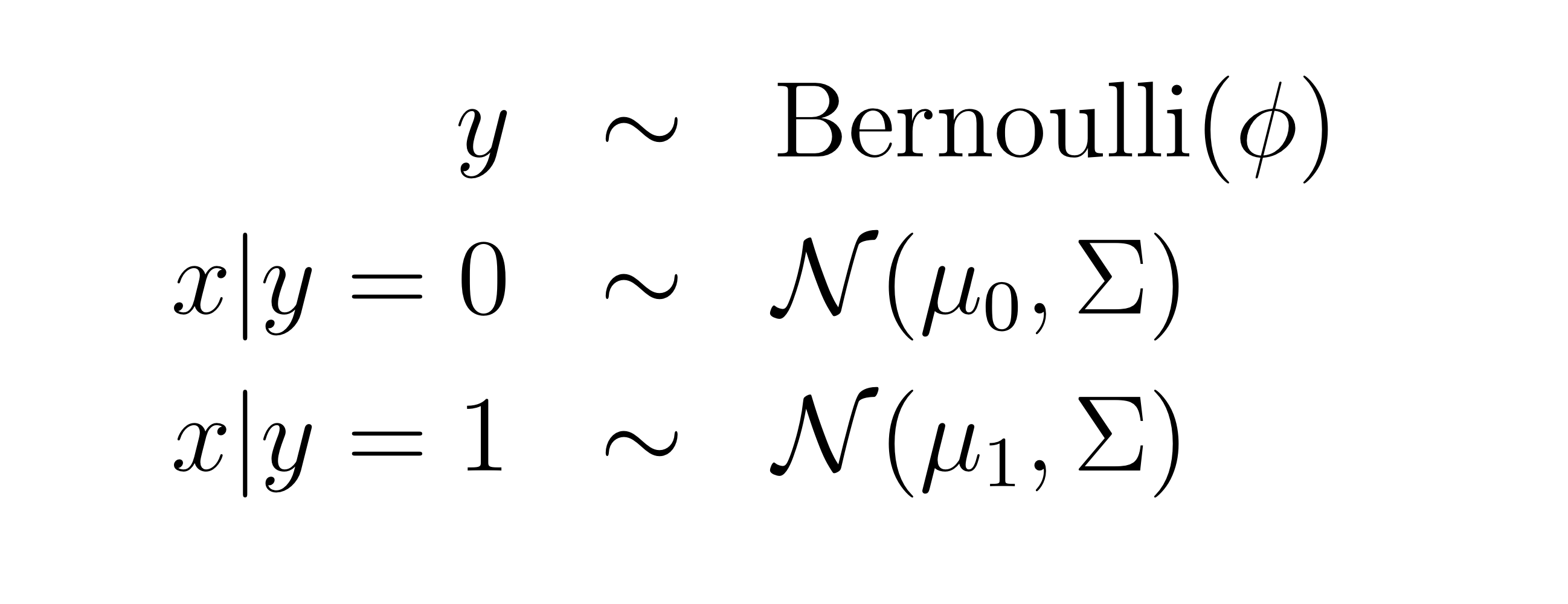
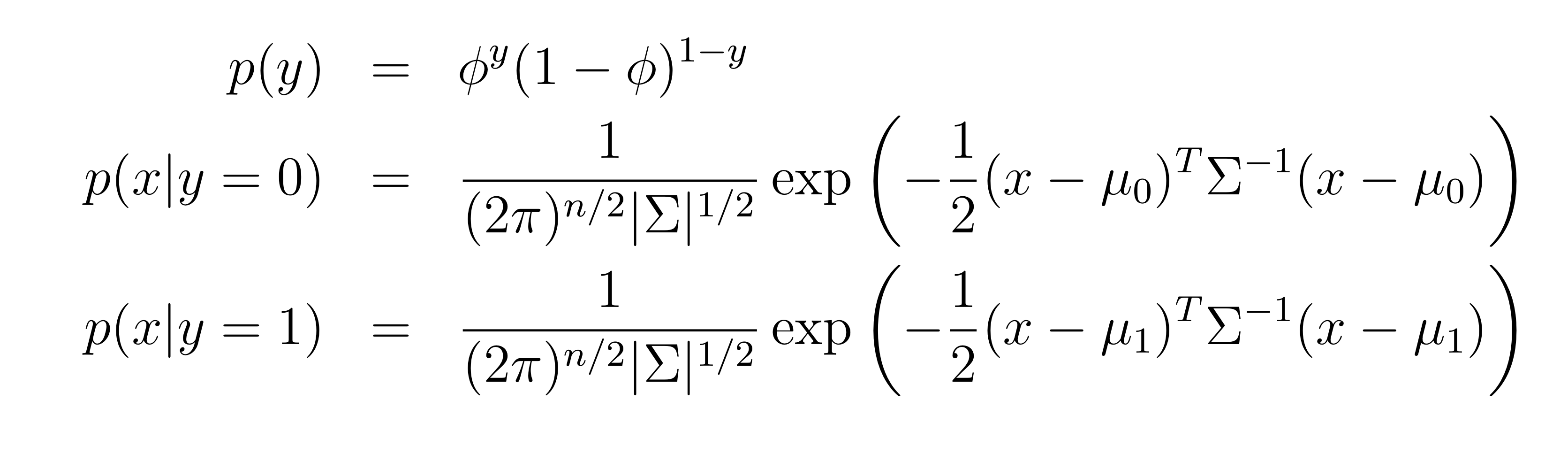
베르누이 분포를 따를 경우에 likelihood를 위와 같이 쓸 수 있다. 평균 벡터 $u_0,u_1$은 다르더라도 $\Sigma$ 는 일반적으로 같게 적용한다. 물론 다르게 해도 잘 된다.

$\frac {\sigma}{\sqrt{2\pi}}exp(-\frac 1 2(\frac {x-\mu}{\sigma})^2)$ 의 행렬 form으로 기억해도 좋다.

위에 log-likelihood를 적용해보자.

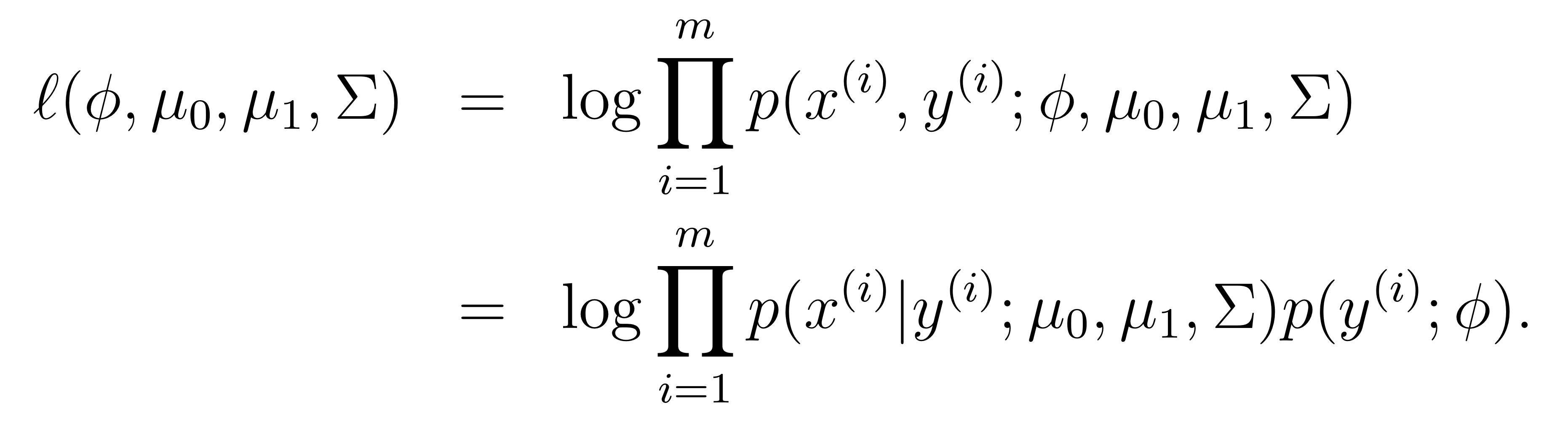
위 log likelihood를 각각의 파라미터에 대해 최대화하면, 다음과 같은 식을 얻을 수 있다.

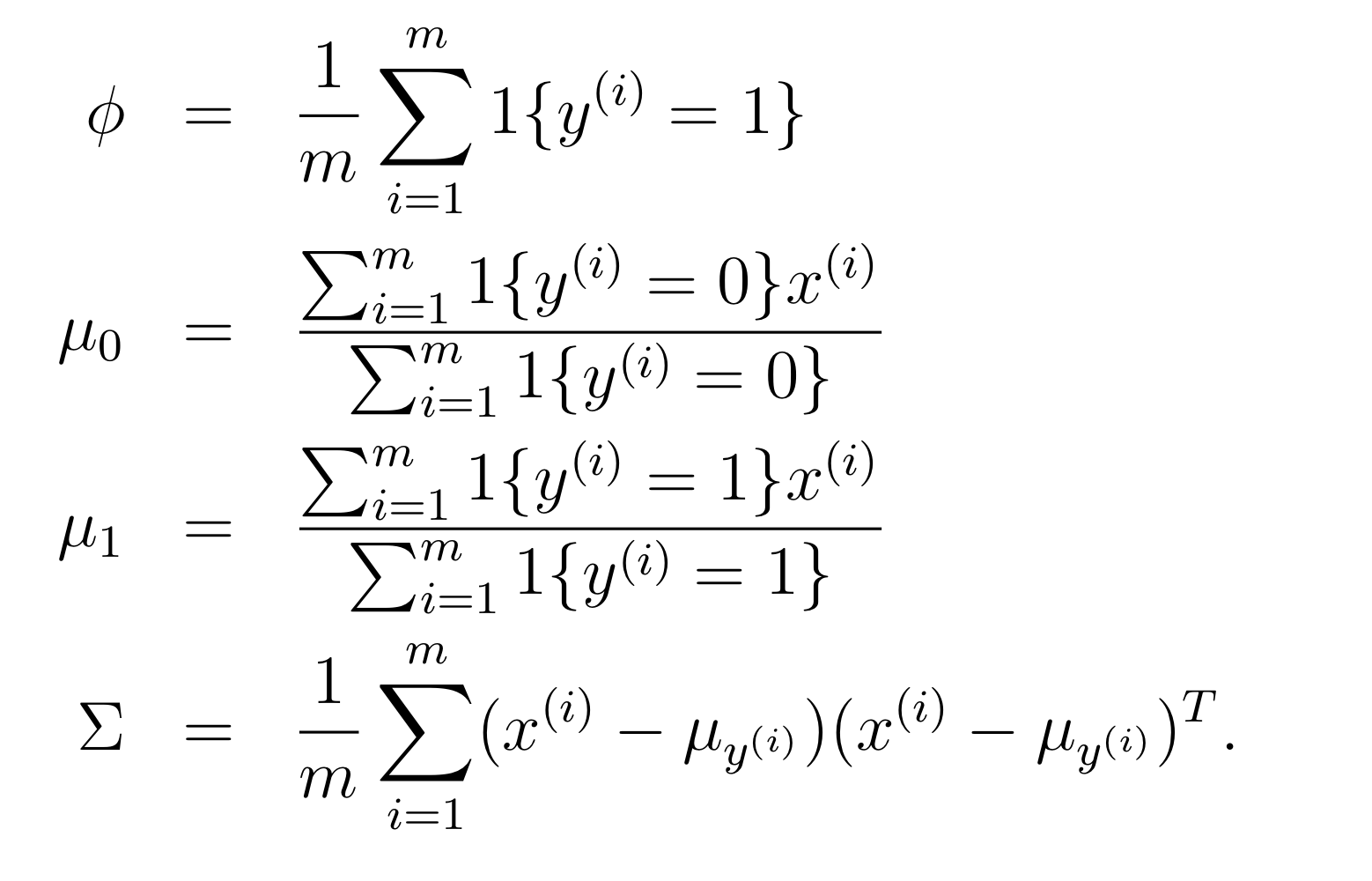
첫번째 $\phi$ 는 당연히 그렇게 될 수 밖에 없고
두번째 $\mu_0$ 의 경우에의 식은 $y=0$ 에 해당하는 샘플들의 평균을 의미하는데, 그렇게 했을 때 likelihood 가 커질 것이라는 것을 쉽게 예상해볼 수 있다.
세번째도 마찬가지다.

Generative Vs Discriminative Comparision

GDA 와 Logistic regression은 연관이 있다.
우리가 $p(y=1|x;\phi,\mu_0,\mu_1,\Sigma)$ 를 $x$에 대한 함수로써 생각한다면. 우리는 이것이 exponential family에 의해 $\frac {1} {1+exp(-\theta^Tx)}$ 으로 나타날 수 있음을 알 수 있다. (binary classification)

여기서 $\theta$는 $\phi,\mu_0,\mu_1,\Sigma$ 으로 이루어진 적절한 함수라고 가정할 수 있다.

그러면 어떤 걸 사용하는게 좋을까? GDA를 사용하는게 좋을까 Logistic regression을 사용하는게 좋을까. 일반적으로 이 두개는 다른 경계선을 만든다.

위에서 살펴본 바로는 $p(x|y)$ 가 다변수 가우시안(분산이같은) 이라면 $p(y|x)$는 logistic function을 따를 수 밖에 없다. 그러나 그 반대는 성립하지 않는다. $p(y|x)$가 logistic function이라고 해서 $p(x|y)$ 가 다변수 가우시안 분포를 가지지는 않는다. 여기서 다음과 같은 점을 알 수 있다.

GDA는 Logistic regression보다 강한 modeling assumptions 을 가지고 있다.

만약 데이터에 대한 assume(다변수 가우시안분포이고 분산이 같다)이 정확하다면, GDA는 더 좋은 성능을 보일 수 있다.
asymptotically effecient 하다고도 표현하는데, 이 말은 데이터가 무한정 많아진다면, GDA보다 더 좋은 알고리즘은 없다는 뜻이다. (중심 극한 정리와도 연관되는 내용인 것 같다)

반면에, logistic-regression은 훨씬 더 robust하고 틀린 assumption에 대해서 더 robust 하고 덜 민감하다.

어떤 데이터가 실제로는 포아송 분포인데 가우시안 분포라고 가정하고 GDA를 사용한다면, 안좋은 결과를 내겠지만 만약 logistic-regression을 사용한다면 꽤 괜찮은 결과를 보여준다.

왜냐하면 포아송 분포 또한 $p(y|x)$ 가 logistic 하기 때문이다.

데이터가 실제로 gaussian 인 경우, 혹은 거의 무한한 경우
-> GDA better
데이터가 gaussian 분포가 아닌경우
-> logistic regression better

Naive Bayes

naive는 한국어로 순진하다는 뜻이다. Naive Bayes는 뭘까?
GDA 에서 feature 벡터 x는 연속적인 실수 벡터였다. 이제 feature 벡터가 이산적인 값인 경우를 생각해보자.

예시로 text classification 문제를 생각해보자. 예를 들어 스팸 메일을 분류하는 문제를 생각해 볼 때, 우리는 어떤 메일을 feature 벡터로 표현할 수 있다. 그 feature 벡터는 사전에 등록되어 있는 단어들의 개수와 같을 것이다.(혹은 가장 많이 사용되는 10000개의 단어 등으로 축소시킬 수도 있다)

아래 $x$ 가 make a buy 라는 메일이라고 가정해보자.

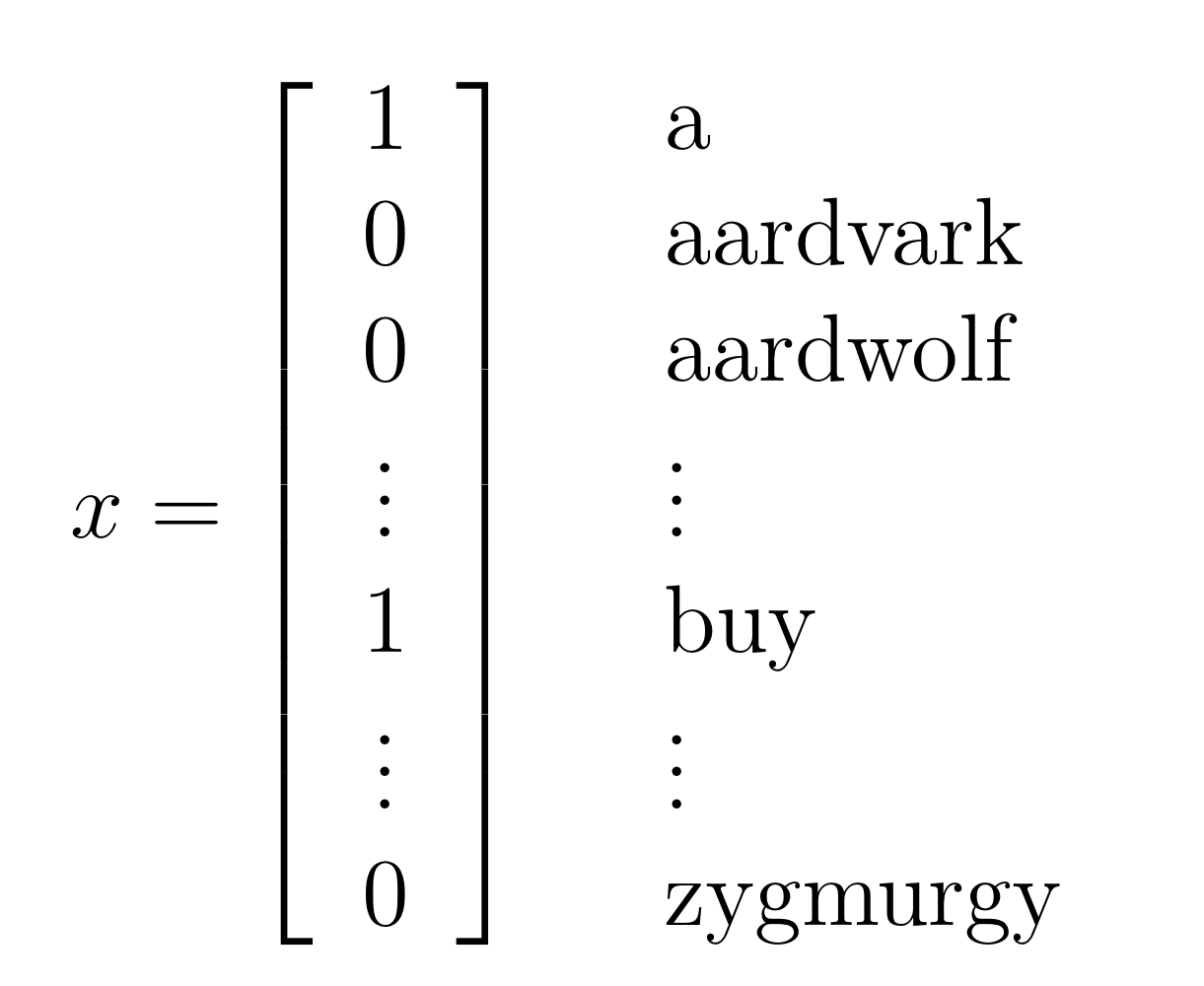
그리고 뽑은 어떤 샘플을, 그 단어를 가지고 있다면 해당 인덱스에 있는 값을 1로, 그 단어가 없다면 해당 인덱스에 있는 값을 0으로 표현할 수 있다.

이렇게 feature vector로 encoded 된 것을 vocabulary 라고 부른다. $x$ 의 차원이 vocabulary 의 크기와 같다고 할 수 있다.

이제 feature vector를 만들었으면, generative model 을 만들어보자. 그러나 만약 단어가 50000개만 있다고 하더라도.. 가능한 경우의 수가 $2^50000$ 가지가 된다. 그리고 파라미터는 $2^50000-1$개가 될 것이다..(bias)

파라미터가 너무 많다. 그래서 우리는 아주 강력한 assumption을 할 것이다.
만약에 모든 feature 들이 주어진 $y$에 대해서 조건부 독립이라면, 우리는 이 assumption을 Naive Bayes assumption (NB) 라고 부른다. 그리고 이렇게 해서 만든 분류기를 Naive Bayes classifier. 라고 한다.

p(x|y)를 모델링 할 때, 모든 feature vecter 들이 주어진 y 에 대해 conditionally independent 하다면, 이것을 Naive Bayes assumption이라고 부르고 이렇게 만들어진 분류기를 Naive Bayes classifier라고 부른다.

예를 들어 만약 $y=1$이 스팸 이메일이라고 한다면. "buy"라는 단어와 "price"라는 단어가 서로 연관이 없다는 뜻이다. 수학적으로 표현했을 때
buy $= x_{2087}$, price $= x_{39831}$ 이라고 한다면
$p(x_{2087}|y) = p(x_{2087}|y,x_{39831})$ 이라고 말할 수 있다.

이 말은 buy 와 price라는 단어가 서로 독립적이라는 의미가 아니다. 다만 y라는 조건이 주어졌을 때 buy 와 price라는 단어는 독립적이라는 뜻이다.

만약 모든 feature 들이 $y$에 대해 조건부 독립이라면, 다음과 같이 쓸 수 있다.

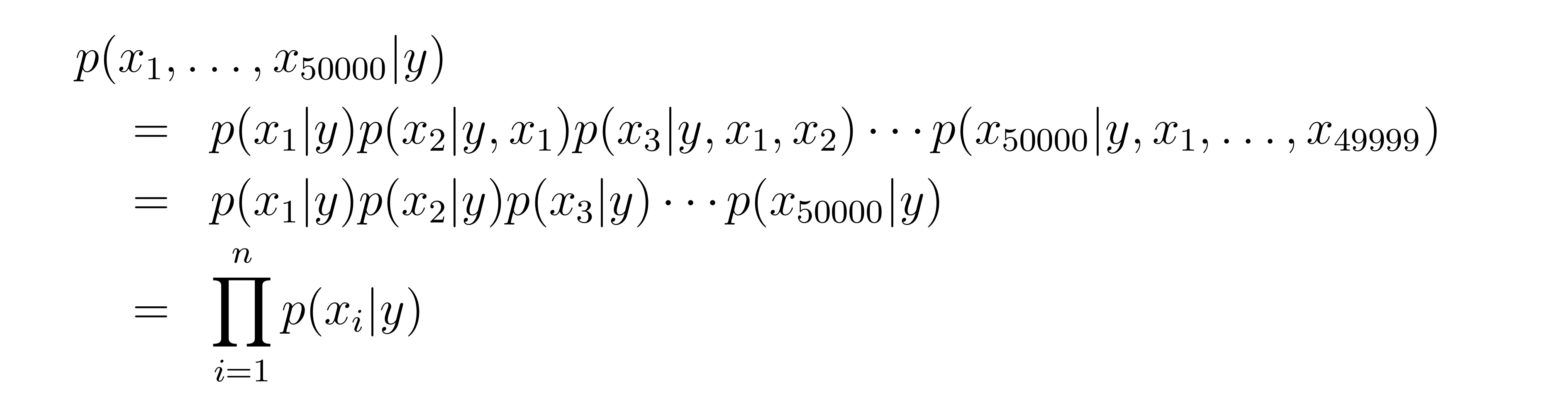
두번째 등호에서 NB assumption이 사용되었다.

우리 모델을 다음과 같이 parameterized 될 수 있다.
$\phi_{i|y=1} = p(x_i=1|y=1), \phi_{i|y=0}=p(x_i=1|y=0)$
and $\phi_y=p(y=1)$

training set을 $\{(x^i,y^i);i=1,\dots,m\}$ 로 설정한 후
우리는 joint likelihood를 다음과 같이 적을 수 있다.

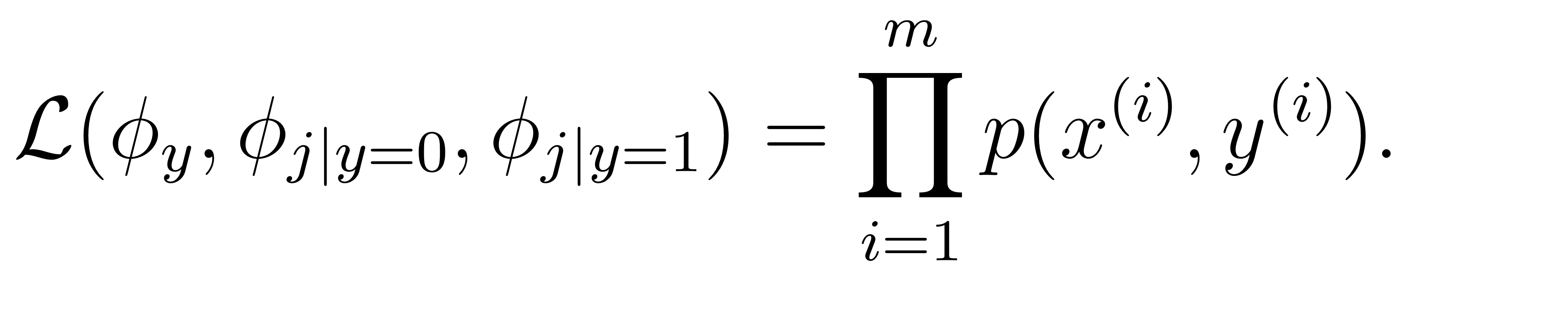
스팸 메일이 발생할 확률과 스팸메일일 경우 각각의 feature들의 확률, 그리고 스팸메일이 아닐 경우 각각 feature들의 확률로, $x^{(i)}$ 샘플과 $x^{(i)}$라는 결과가 동시에 발생할 확률 분포를 만들 수 있다.

우리의 목표는 오른쪽의 의 확률값을 최대화 하는 $\phi$를 찾는 것으로 볼 수 있다.

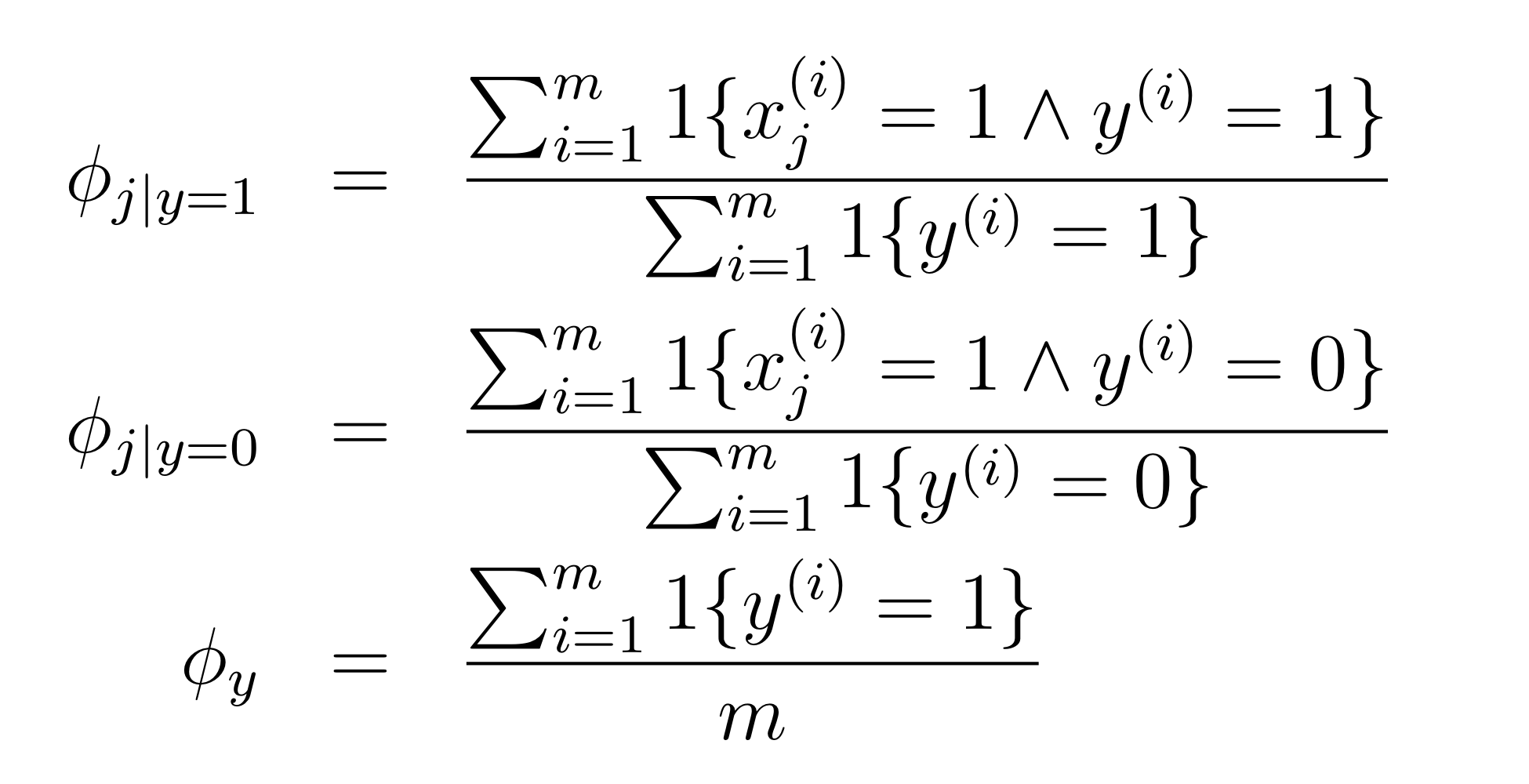
likelihood를 최대화 시키는 $\phi$들을 위와 같이 적을 수 있는데, 첫번째 식에서 모든 스팸 메일의 개수로 j 번째 feature 가 1이면서 동시에 스팸메일인 샘플의 개수를 나누고 있다. 즉 j번째 feature 에 대해 스팸 메일일 기댓값을 구하고 있다.

다른 식들도 어렵지 않게 해석할 수 있다.
위 식을 사용해 모든 파라미터들을 fit 했으면, 베이즈 법칙을 사용해 prediction을 수행할 수 있다.

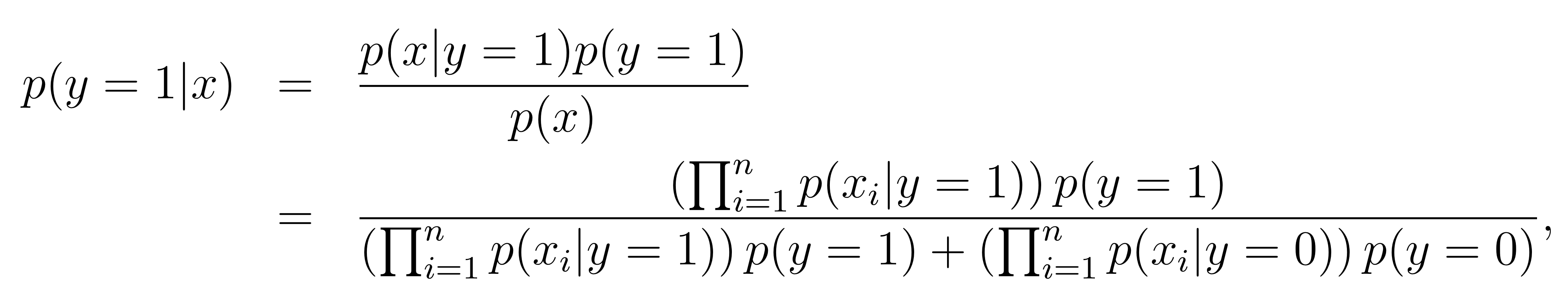
위에서는 Bernoulli 분포라고 assume 한 경우를 생각했다. 그러나 Multinominal distribution인 경우에도 우리는 Naive Bayes를 적용할 수 있다. 예를 들어 스팸메일인 지 아닌 지 를 친구메일, 기업메일, 광고메일 등으로 구분하는 Multinominal한 문제를 생각해볼 수 있다. 이런 경우에 해당하는 feature 를 0이나 1이 아니라 2, 혹은 3으로 설정할 수 있다.

만약 continuous-valued attributes 가 multivariate normal distribution에 의해서 모델되지 않는다면 feature들을 이산적으로 분류하고 NB를 사용하는 것이 더 효과적일 수도 있다.

근데 문제가 있다. 만약 어떤 $p(x_i|y=1)$ 이 0이 되어버린다면.. 어떤 문제가 발생할 수 있다. 이 문제를 해결하기 위해 Laplace smoothing 이라는 것을 사용한다. 다음 포스트에서 확인해보자

Laplace smoothing

NIPS 라는 협회에 논문을 낸다고 생각해보자. 이 협회에 매일을 보내고 난 다음에 돌아오는 메일에 대해 위의 스팸 분류기는 어떻게 분류할까?
아마 이전에는 NIPS라는 협회로부터 메일을 받은 적인 단 한번도 없을 것이다. 그 상태에서 내가 받았던 메일을 기준으로 Naive Bayes를 사용해 Maximum likelihood를 사용했을 때 만약 NIPS가 6017번째로 라벨링되어있는 단어라면 그 단어가 스팸일 확률은 0일 것이다. 또 스팸이 아닐 확률도 0일 것이다.
즉 $P(x_{6017}=1|y=1) = \frac {0}{\#y=1} ,P(x_{6017}=1|y=0) = \frac {0}{\#y=0}$

허나 이건은 조금 이상하다

통계적으로 어떤 현상이 이전에 일어난걸 보지 못했다고 해서 해당 확률이 0이라고 가정하는 것은 좋지 않은 생각이다.

이것을 기준으로 어떤 메일을 받았을 때 스팸일 확률을 구한다면,

이 된다. 왜냐하면 분자의 $P(x=1|y)$ 는 모든 $x_1 \sim x_{10000}$ 까지의 확률을 곱한 것이고, $P(x_{6017}=1|y=1)$ 은 0이기 때문이다. 분모도 마찬가지로 0+0이 된다. 0으로 나누는 오류가 생기게 된다.

0으로 나누는 오류는 차치하고서라도, 어떤 일을 한 번도 본적이 없다는 이유로 확률이 0이라고 가정하는 것은 좋지 않은 일이다. 내가 하얀색 까마귀를 본 적이 없다는 이유로 하얀색 까마귀가 있을 확률을 0이라고 해도 괜찮을까?

이러한 문제를 해결하는 것이 Laplace smoothing이다.

Laplace smoothing은 어떤 사건이 일어났던 횟수에 +1을 해준다.
예를 들어 위에서 NIPS라는 단어가 나타난 횟수는 0회였지만, 의도적으로 +1을 더해주는 것이다. 이렇게하면 확률이 0이되어 버리는 문제를 해결할 수 있다.

위 수식에 Laplace smoothing을 적용하면 아래와 같다.

스팸 문자가 아닐 때 $i$ 번째 단어가 있을 확률을 구할 때 우선 분자에서 해당 단어가 나타나는 갯수에 +1을 해주고 분모에서는 스팸 문자일 때 해당 단어가 나타나는 경우, 그리고 스팸 문자가 아닐 때 해당 단어가 나타나는 경우 두 가지 케이스에 대해서 각각 +1을 해준다. 결과적으로는 스팸문자가 나타나는 횟수 + 2가 된다.

위에 NIPS의 경우에는 확률이 0.5가 된다. 한번도 나타난 적이 없었기 때문에 중립을 유지하는 0.5는 합리적으로 보인다.

Event Model