SVM에 대한 이야기를 해보겠다. 강의내용은 되게 러프해서 내가 이전에 정리해둔 글과 같이 조금 자세하게 정리해보겠다.# SVM-BASE
SVM이란 Support Vector Machine의 약자이다.
SVM은 Classification을 위한 ML Algorithm의 하나인데, 여백(Margin)을 이용하여 일반화 능력을 향상시킨다.
왜냐하면 기존의 Classification은 경계선과 데이터간의 관계를 고려하지 않았는데, SVM은 이 두개의 관계를 고려했기 때문이다. SVM에서는 경계선이 Test Data를 잘 구분 해주더라도, 조금 더 학습을 진행시켜 경계선이 Train Data로부터 멀리 떨어지도록 만든다(여백을 증가시킨다).
북한과 남한의 경계를 가를 때 딱 붙여서 갈랐다면 안 좋은 일이 생겼을 것이다. 두 개의 경계를 잘 가르기 위해서는 중간에 DMZ라고 하는 완충지대가 필요하다. DMZ를 SVM에서 말하고 있는 여백이라고 비유해볼 수 있다.
SVM은 비록 DL에 밀려 시들하지만 수학적으로 봤을 때 아름답기 때문에 ML을 공부한다면 알아볼 필요가 있다.
SVM은 NN과 비교했을 때 훨씬 더 다루기 쉽고 우리가 완전히 정복한 이론이다. 이 것을 이해한다면 생각의 폭이 더 넓어질 것이다.
알아야 하는 선형대수 지식
먼저 알아야 하는 선형대수 지식이 있다.
선형대수에서 직선의 방정식을 벡터의 내적형태로 표현할 수 있다.
w=[ab],d=[xy]
ax+by=[ab][xy]=w⊺d=c
이렇게 내적의 형태로 표현하면 훨씬 더 간단하게 표현할 수 있다.
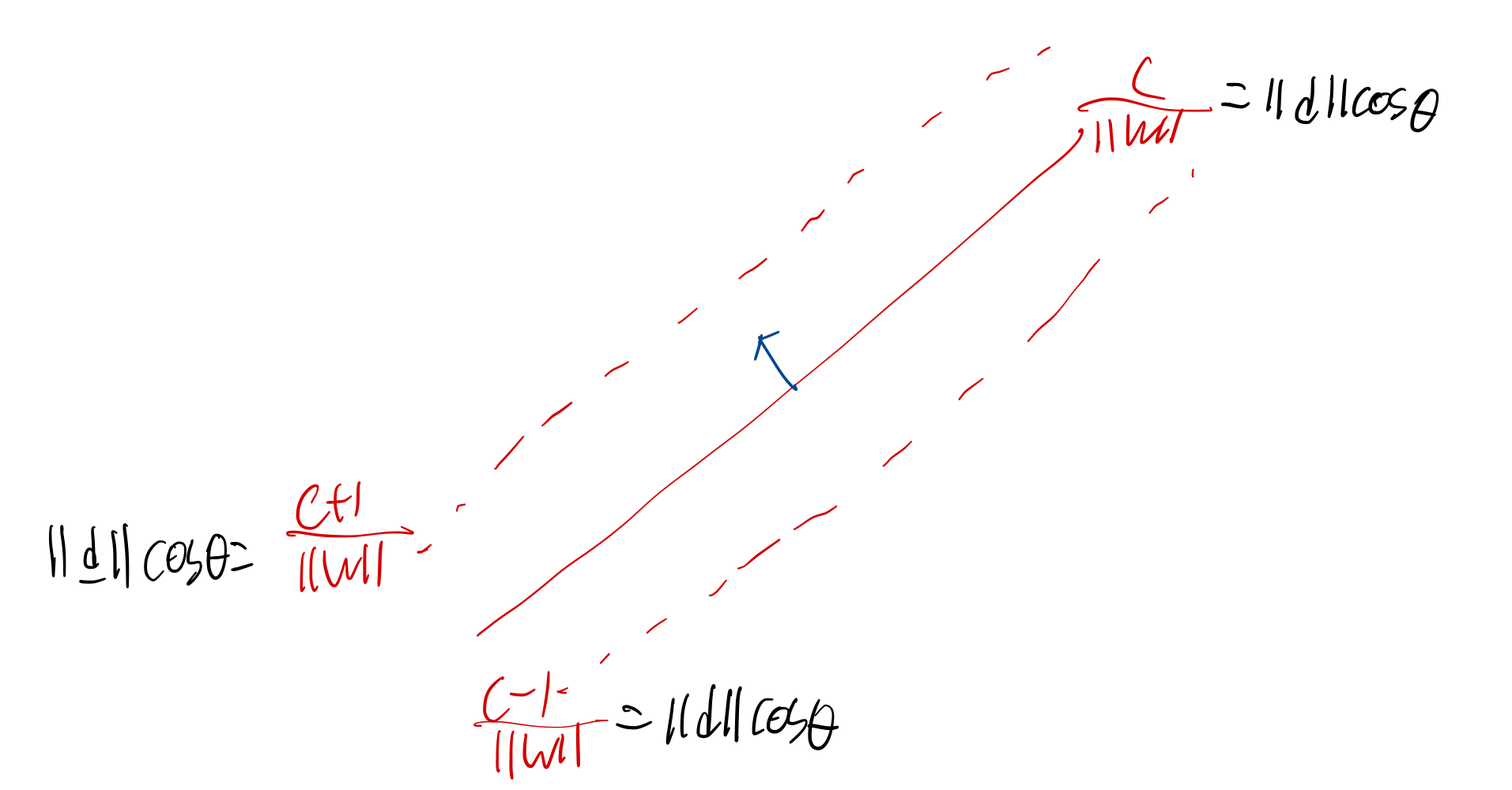
그리고 w⊺d=c는 우리가 ∥w∥∥d∥cosθ=c 로 표현할 수 있다.
여기서 식을 변형해 다음과 같이 살펴보자.∥d∥cosθ=∥w∥c
여기서 우변을 하나의 상수처럼 취급할 수 있다.
만약에 ∥w∥가 1이라고 둔다면 (w 는 법선벡터이므로, 크기는 중요하지 않다. )
∥d∥cosθ=c
이렇게 되는데
이때 d의 자취를 그려보면, w 벡터에 정사영 했을 때 그 크기가 c 인 벡터들의 모임이므로,
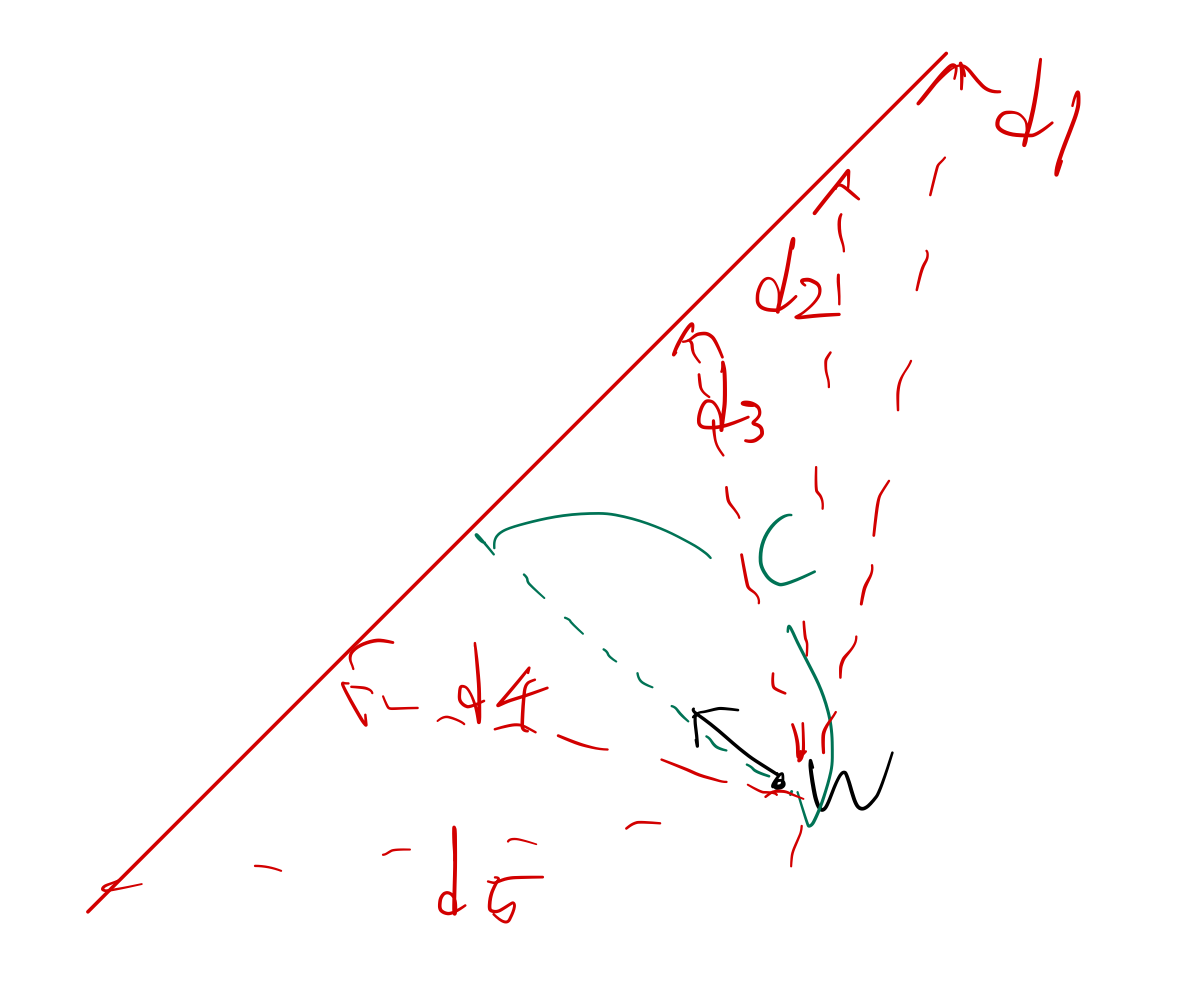
다음과 같이 빨간 직선이 d의 자취로 그려진다. 그리고 이것이 곧 직선의 방정식이 된다.∥d∥cosθ=∥w∥c
즉 우리가 이 식의 그래프를 우변을 만족하는 d의 자취로도 해석할 수 있다.
만약에 어떤 점이 이 직선보다 위에 있다면 어떨까?
위 식의 d 대신에 그 점을 집어넣으면 된다. 그리고 그렇게 한다면
위 식의 좌변은 우변보다 커지게 될 것이다.
만약 아래에 있다면 좌변은 우변보다 작아지게 될 것이다.
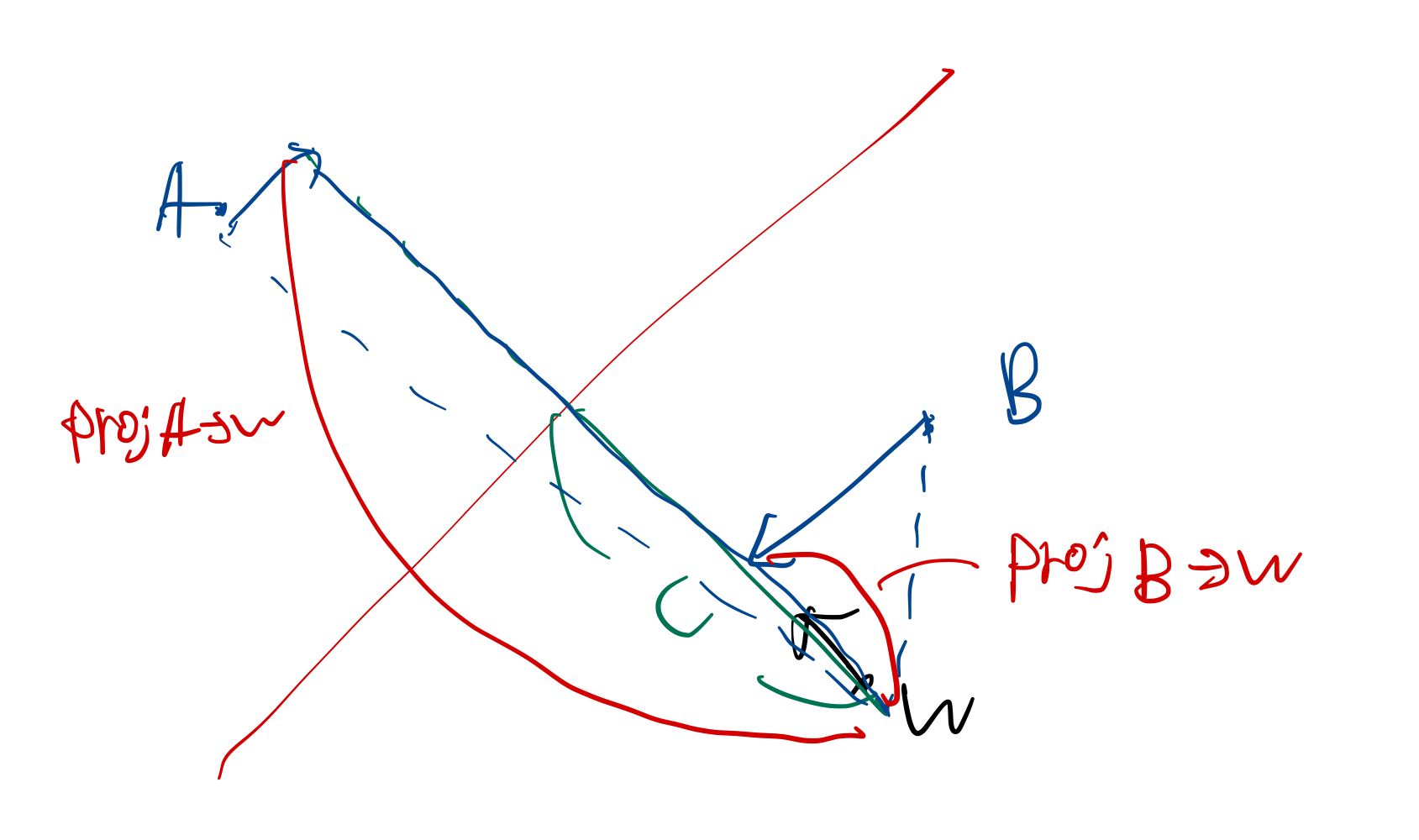
점 A는 직선보다 위에 있고 점 B는 직선보다 아래에 있다.
∥w∥가 1일때
점 A에 해당하는 벡터를 w에 정사영 시킨다면 그 값은 c 보다 커지게 된다.
∥A∥cosθ >∥w∥c=c
점 B에 해당하는 벡터를 w에 정사영 시킨다면 그 값은 c 보다 작아지게 된다.
∥B∥cosθ<∥w∥c=c
∥w∥가 1이 아닌 경우로 일반화하고 싶으면 c를 ∥w∥c으로 변경하면 된다.
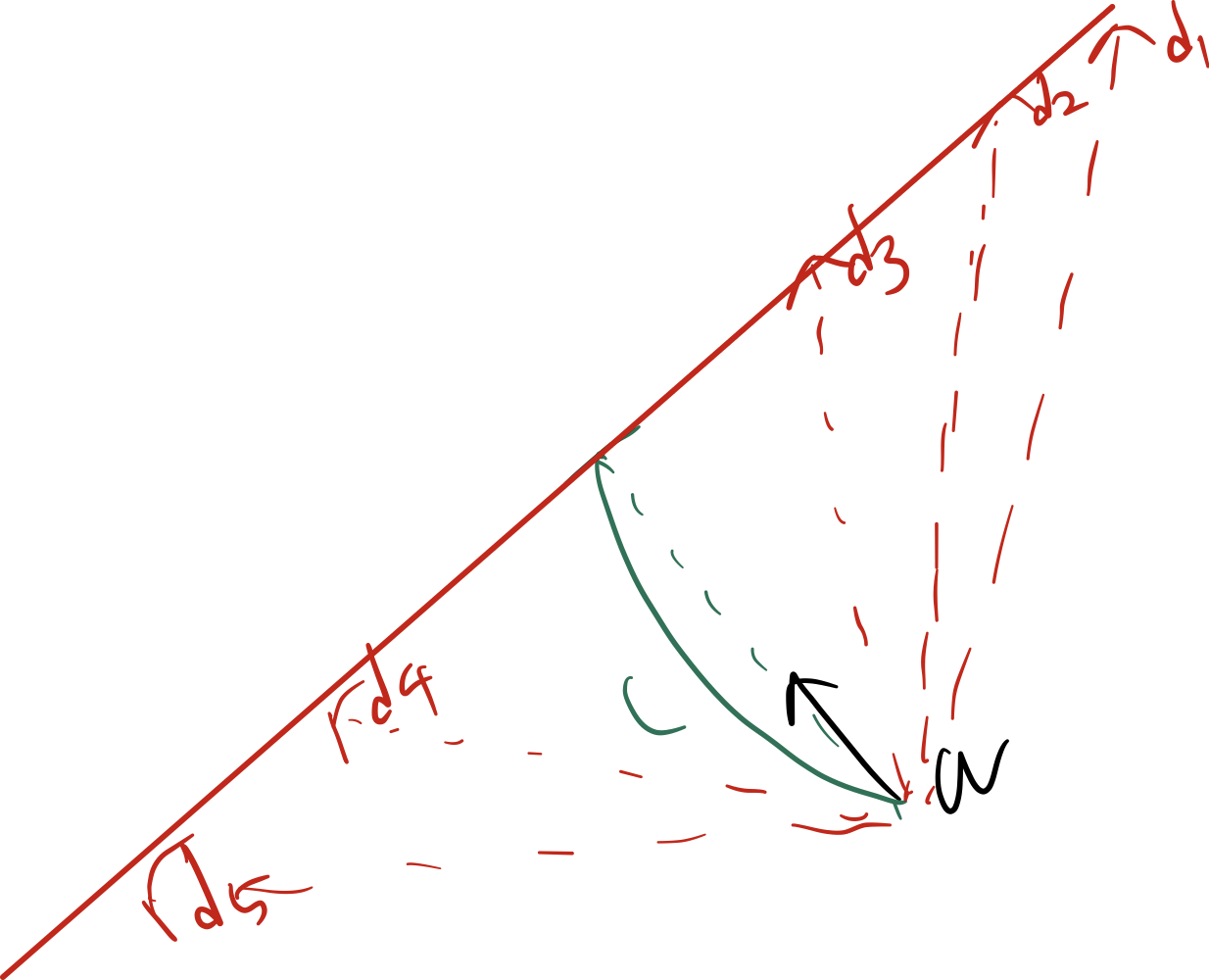
이제 이 그림을 이해해보자, 굵은 빨간 기준 경계선이 있고, 위 아래로 같은 거리에 빨간 점선이 두가지 있다.
위 빨간 점선에 해당하는 식은 다음과 같이 쓸 수 있다. 우리는 w의 값을 자유롭게 조정할 수 있으므로, 분자에 어떤 값이 더해지든 큰 상관은 없다. 하지만 편의성을 위해 1을 더한다.
∥d∥cosθ=∥w∥c+1
∥d∥cosθ=∥w∥c 보다 w 에 정사영을 내렸을 때 그 값이 더 큰 벡터들의 자취로 볼 수 있다.
아래 빨간 점선에 해댱하는 식은 다음과 같이 쓸 수 있다.
∥d∥cosθ=∥w∥c−1
그리고 이 식도 마찬가지로, w에 정사영을 내렸을 때 그 값이 더 작은 벡터들의 자취로 볼 수 있다.
굵은 선에 비해 같은 양이 커지고 작아졌으므로, 이 직선들 간의 간격은 같다.
그리고 이 두 점선 사이의 거리는 우변끼리 빼주면 ∥w∥2 다음과 같이 쓸 수 있다.
SVM에서 margin을 말할 때 ∥w∥2를 사용하게 된다. 이것을 잘 보자.
SVM LINEAR
선형 분리 가능한 문제에 대해서 먼저 생각해보자.
SVM의 단계는 다음과 같다.
- 데이터를 오류없이 분류하도록 w 정한다.
- 정해진 직선의 방향w에 대해, 직선으로부터 가장 가까운 샘플까지의
거리가 같게 되도록 바이어스 c를 정한다.
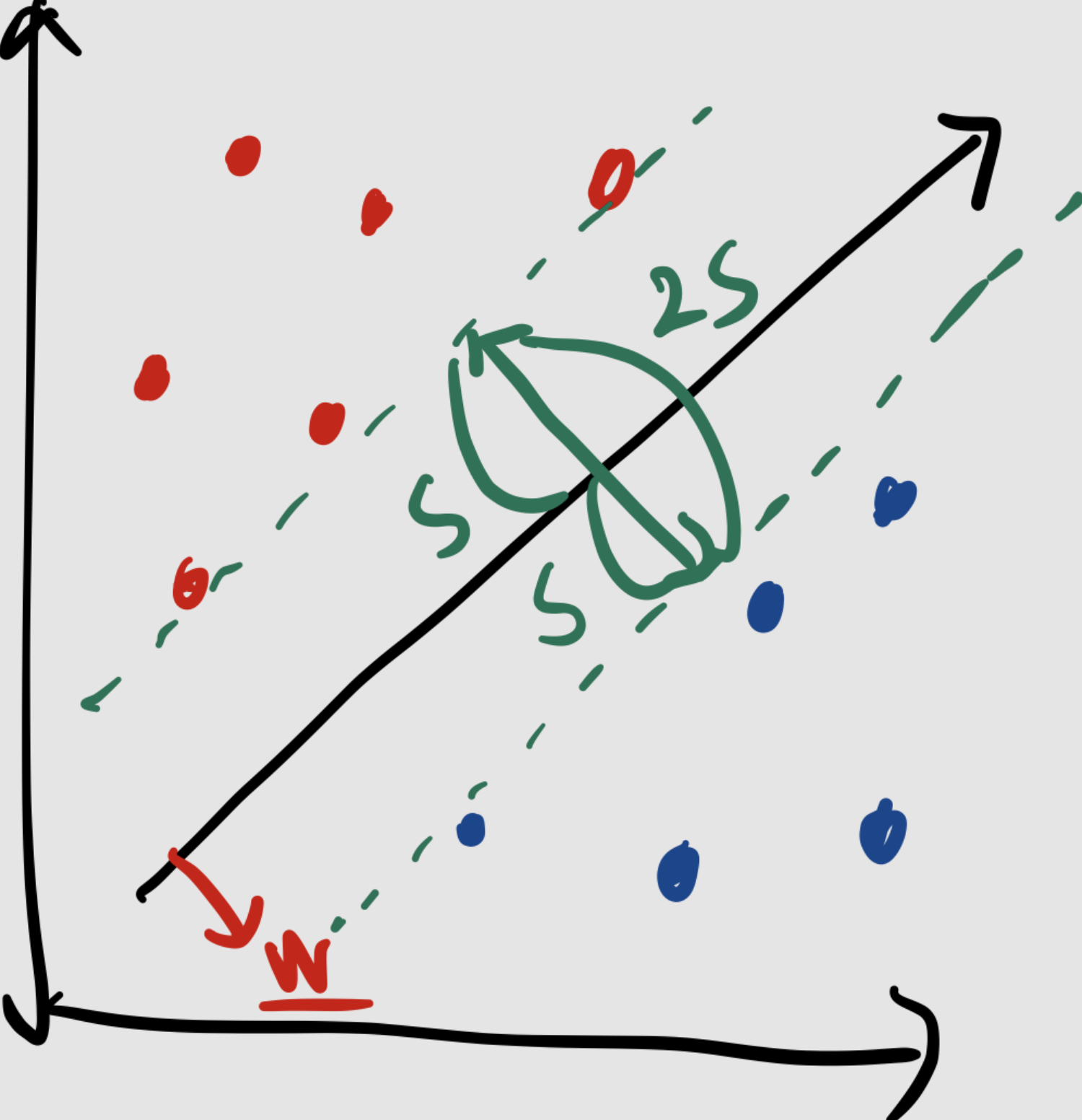
위 그림에서 직선과 가장 가까운 빨간색 샘플까지의 거리와 직선과 가장 가까운 파란색 샘플까지의 거리가 같도록 직선을 결정하면 된다.
여기서 이 초록색 띠의 너비 (2s)를 마진이라고 부른다.
SVM은 여기서 이 마진의 크기를 최대로 하는 결정 초평면을 구하는 알고리즘이다.
그리고 이전 시간에 margin을 ∥w∥2으로 나타낼 수 있음을 배웠다.
마진을 최대화 하는 것이 우리의 목표이다. 그런데 마진을 최대화 하는 것은
∥w∥를 최소화 하는 것과 같고, 이것을 최소화 하는 것은
21∥w∥2를 최소화 하는 것과 같다. 이렇게 쓰는 이유는 단순히 계산상의 편의 때문이다.

우리는 마진을 최소화 하는 것도 중요하지만, 샘플들이 잘 분류되도록 하는 것도 중요하다.
위 그림에서 왼쪽 점선띠(c+1) 위에 있는 샘플들은 1로 분류하고
오른쪽 점선띠(c−1) 아래에 있는 샘플들은 -1로 분류해야한다.
이 것을 다음 식으로 표현할 수 있다.
훈련 집합을 {(x1,y1)⋯(xn,yn)} 으로 표현한다면,
w⊺xi≥c+1 ,∀yi=1 ← d(xi)≥1 ∀yi=1
w⊺xi≤c−1 ,∀yi=−1 ← d(xi)≤−1 ∀yi=−1
이 식을 만족시켜야 한다. 이 식의 의미는,
w⊺xi≥c+1 ,∀yi=1 를 만족시키는 모든 xi에 대해서,
그에 해당하는 yi를 1로 분류해줘야 한다는 뜻이다.
다른 식도 마찬가지로 해당 식에 대해서 yi를 -1로 분류해주라는 뜻이다.
식을 바꿔주면
w⊺xi−c−1≥0 ,∀yi=1
w⊺xi−c+1≤0 ,∀yi=−1 로 바꿔줄 수 있다.
이것을 간단하게 바꿔주면 다음과 같은 식으로 쓸 수 있다.
yi(w⊺xi−c) 는 항상 양수이므로, (음수 곱하기 음수 또는 양수 곱하기 양수 이므로)
$y_i(\underline w^\intercal \underline x_i -c)-1 \geq 0 $ 를 만족시키도록 하면 된다.
즉 우리는 문제를 다음과 같이 쓸 수 있다.
Minimize:J(w)=21∥w∥2
Subject to:yi(w⊺xi−c)−1≥0,i=1,2,3,4,5,⋯n
or
Subject to:yi(c−w⊺xi)+1≤0,i=1,2,3,4,5,⋯n
Meaning of Support Vector
서포트 벡터의 의미가 무엇인가?
그것은 경계선에 있는 점들의 위치벡터를 의미한다.
즉 yi(w⊺xi−c)−1=0 을 만족하는 xi벡터들을 의미한다.
(a.k.a w⊺xi−c−1=0 혹은w⊺xi−c+1=0 를 만족시키는 Vector xi)
Lagrangian in SVM
위 Problem을 라그랑지안을 통해서 표현할 수 있다.
f(x)를 최소화하면서 g(x)≤0 을 만족하는 문제를 풀 때,
라그랑지안을 L(x,λ)=f(x)+μg(x) 로 쓸 수 있다.
f(x)를 최소화하면서 g(x)≥0 을 만족하는 문제를 풀 때는
L(x,λ)=f(x)−μg(x) 이렇게 쓴다. 이번에는 이걸로 아래에 notation 해보겠다.
이를 SVM에 적용하면 (μ 를 α로 표현) (c를 b로 표현)
L(w,b,α)=21∥w∥2−i=1∑nαi(yi(w⊺xi−b)−1) 와 같이 쓸 수 있다.
그리고 이 라그랑지안 문제를 풀면 된다.
푸는 첫번째 방식은 KKT를 사용해 그라디언트가 0이 되도록하는 것을 구해서 연립하는 것이다.
∂w∂L(w,b,α)=0 ⇒w=i=1∑nαiyixi
∂b∂L(w,b,α)=0⇒i=1∑nαiyi=0
∂α∂L(w,b,α)=0⇒i−1∑n(yi(w⊺xi−b)−1)=0
αi≥0
두번째 방법은 Dual Problem을 이용하는 것이다.∇w,bL을 이용하여 w,bargminL 을 찾은 후
∇q(α)를 통해 αargmaxq 를 찾는다.
첫번째를 풀면
w=i=1∑nαiyixi
i=1∑nαiyi=0 이 두가지 식이 나온다.
그리고 w=i=1∑nαiyixi를 원래 식 L에 대입하면
q(α)=21∥i=1∑nαiyixi∥2−i=1∑nαi(yi((j=1∑nαjyjxj)⊺xj−b)−1)이 나오고 정리하면
q(α)=21i=1∑nj=1∑naiajyiyjxi⊺xj−i=1∑nj=1∑naiajyiyjxi⊺xj+i=1∑naiyib+i=1∑nαi 이다.
여기에 i=1∑nαiyi=0 이므로 대입하면 b를 없앨 수 있다.
q(α)=i=1∑nαi−21i=1∑nj=1∑naiajyiyjxi⊺xj 이렇게 쓸 수 있다.
여기서 문제를 다음과 같이 간단하게 할 수 있다.
i=1∑nαiyi=0를 만족하고,
αi≥0 i=1,2,3,4,5 를만족하면서,
q(α)=i=1∑nαi−21i=1∑nj=1∑naiajyiyjxi⊺xj 를 최대화 시켜라.
SVM SOFT MARGIN
지금까지 우리가 배운 SVM은 HARD MARGIN SVM이다.
여백 안에 있는 data에 대해서 오차를 허용해 주지 않는 SVM을 뜻한다.
여기서 다음 데이터를 어떻게 잘 구분할 수 있을까?
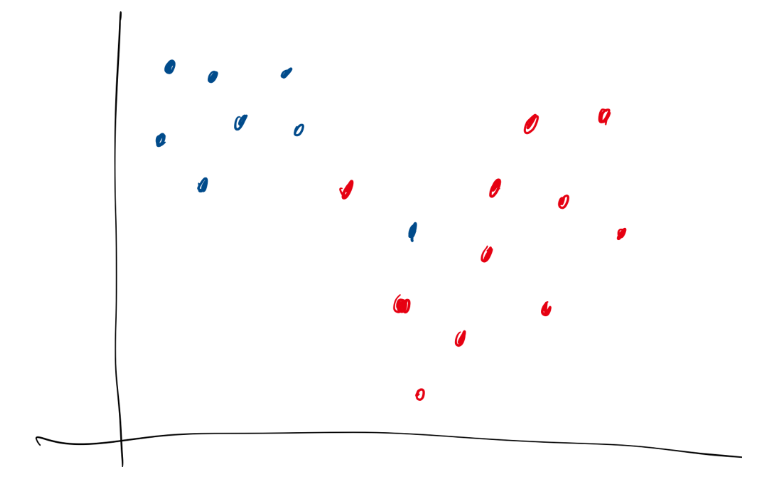
기존의 SVM 방법으로는 이 데이터를 잘 구분해주는 결정경계를 만들 수 없다.(a.k.a 선형분리 불가)
이 데이터 상에서 결정경계를 만들어 주기 위해서는, 여백 안에 데이터들이 어느정도 존재하더라도 허용하게 만들어줄 수 있다.
그래서 ξ라는 새로운 변수를 도입해, 여백 안에 데이터들이 있더라도 어느정도 허용해주도록 할 수 있다.
이것이 실제로 어떻게 적용될 수 있나 알아보자.
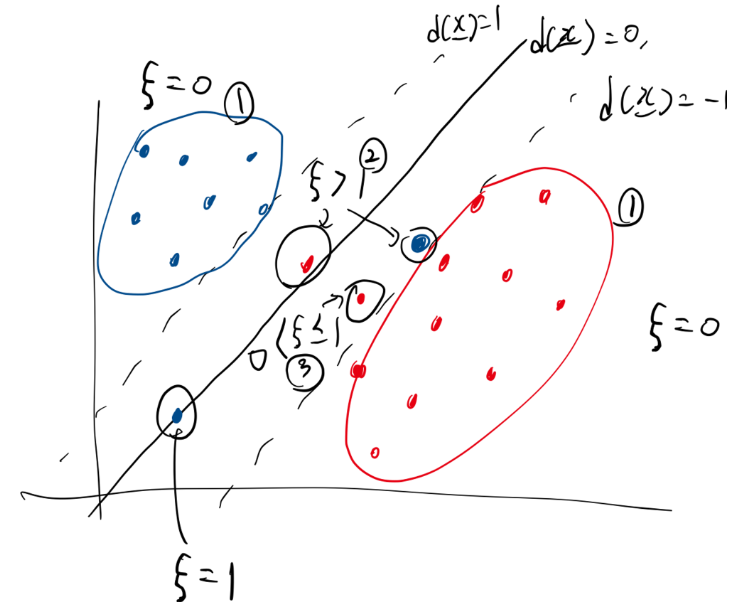
(w⊺xi−c) =0 이것이 결정경계라고 했을 때 (그림에서 직선)
yi(w⊺xi−c)=1 이것이 support vector에 대한 여백의 경계선이다. (그림에서 점선)
그리고 모든 데이터 샘플에 대하여
yi(w⊺xi−c)≥1 이 식이 만족되도록 하면서 마진을 최소화 하는 것이 SVM의 목적이다.
그런데 이 식에 슬랙 변수를 도입해서
yi(w⊺xi−c)≥1−ξi 이렇게 바꾼다면,
여백에 대해서 데이터에 대한 케이스를 다음과 같이 세가지로 나눌 수 있다.
1) 옳게 분류된 경우 (그림에서 1번 동그라미)
yi(w⊺xi−c)≥1 , ξi=0
2) 옳게 분류됐지만 마진 안에 있는 경우 (그림에서 2번 동그라미)
0≤yi(w⊺xi−c)≤1 , 0<ξi≤1
3) 틀리게 분류된 경우 (마진 안에 있는지는 고려 안함)(틀렸으므로) (그림에서 3번 동그라미)
yi(w⊺xi−c)<0 , 1<ξi
1번 케이스의 경우에는 어짜피 잘 분류가 되었으므로 ξi=0인경우라고 할 수 있다.
2번 케이스의 경우에는 분류가 잘 되었지만 마진 안에 있고 0<ξi≤1 인 경우라고 할 수 있다.
3번 케이스의 경우에는 분류가 잘 안되었고 결정경계의 밖에있는 1<ξi 인 경우라고 할 수 있다.
yi(w⊺xi−c)≥1−ξi
이상적인 상황은 모든 점들의 슬랙변수가 0인 상황일 것이다. 그러나 위 그림과 같이 데이터가 항상 선형 분리되도록 주어지지는 않기 때문에, 여백 안에 몇개의 불순물들이 있는 것은 허용해 주어야 한다. 이것을 위해 2번 케이스나 3번케이스와 같은 샘플들에 대해서는 슬랙변수를 0보다 크게 만들어 여백 안에 있거나 결정경계를 벗어나는 경우라도 허용해주는 것이다. 그러나 무턱대고 허용해주다 보면 또 분류가 이상하게 잘 안될 수 있다. 그러니 허용을 해주더라도, 그 허용해주는 범위를 최소화 시켜줘야한다.
자 그러면.. 우리의 목표는 ξi 을 작게 만드는 것이 된다. 왜냐하면 특정 샘플을 허용해주라도, 그 허용해주는 정도를 최소화 해야하기 때문이다. ξi 을 허용해주는 정도로 해석하면 편하다
어떤 데이터 xi 에 대해서 ξi의 의미를 생각해보자
만약 ξi가 1보다 크다는 것은 그 데이터xi 가 오분류 되더라도 그냥 허용하겠다는 뜻이다.
만약 ξi가 0보다 크고 1보다 작으면 그 데이터xi 가 여백안에 있는 것을 허용하겠다는 듯이다.
만약 ξi가 0이라면 그 데이터xi 가 여백안에 있는 것도 허용하지 않고, 여백 밖에서 분류되도록 하겠다는 뜻이다.
데이터를 허용해주지 않으면 분류자체를 못하게 되기 때문에 어느정도의 허용은 필수적이라고 할 수 있다.
슬랙을 이해했다면 우리는 문제를 다음과 같이 다시 정의할 수 있다.
Minimize:J(w,ξ)=21∥w∥2+Ci=1∑nξi
여기서 C는 Hyper parameter로 Minimize를 할 때 어떤 것에 더 중점을 둘 지에 대한 상수이다.
만약 C가 크다면 여백을 최대화 하는 것 보다 ξ를 최소화 하는 것(a.k.a 데이터가 여백안에 있거나 오분류 되는 것을 허용해주지 않는 것)이 더 중요할 것이고,
작다면 21∥w∥2를 최소화(a.k.a. 여백을 최대화) 하는 것이 ξ를 최소화 하는 것 보다 더 중요할 것이다.S.T:
yi(w⊺xi−b)≥1−ξi0≤ξi,i=1,2,…,n
위 조건을 만족하면서 최소화 시키면 된다. (c를 b로 변경)
이를 라그랑주로 바꾸면 다음과 같이 된다.
L(w,b,ξ,α,β)=(21∥w∥2+Ci=1∑nξi)−(i=1∑nαi(yi(w⊺xi+b)−1+ξi)+i=1∑nβiξi)
여기서 w,b,ξ는 우리가 구하고자 하는 변수이고, α,β는 라그랑주 상수이다.
KKT condition을 사용하자. ( i=1,2,3,…,n 이라고 가정)
(Stationarity)
∇L=0
∂w∂L=0⇒w=i=1∑nαiyixi
∂b∂L=0⇒i=1∑naiyi=0
∂ξi∂L=0⇒C=αi+βi
(Complementary Slackness)
αi(yi(w⊺xi+b)−1+ξi)=0
βiξi = 0
(Feasibility)
αi≥0,βi≥0
이렇게 나온다.
이 문제를 쉽게 풀기 위해서 Dual Problem으로 바꿔보자.
라그랑주를 최소화 하는 Primal optimal w,b,ξ 를 찾고
Primal optimal을 대입했을 때의 식을 최대화 시키는 Dual optimal α,β을 찾으면 된다.
자 해보자!
우선
∂w∂L=0⇒w=i=1∑nαiyixi
∂b∂L=0⇒i=1∑naiyi=0
∂ξi∂L=0⇒C=αi+βi 를
L(w,b,ξ,α,β)=(21∥w∥2+Ci=1∑nξi)−(i=1∑nαi(yi(w⊺xi+b)−1+ξi)+i=1∑nβiξi) 여기에 대입해서 정리하면

다음과 같이 바뀐다.
Maximize:q(α)=i=1∑nαi−21i=1∑nj=1∑naiajyiyjxi⊺xj
S.T.:i=1∑naiyi=0, 0≤αi≤C