SOLOv2: Dynamic, Faster, and Stronger 논문 정리

진짜 이 논문은 YOLO 오마주 노린 것 같다 .. 저자는 다른 것 같은데 이번 제목도 그렇고 들어가 있는 Figure도 그렇고 YOLO랑 넘나 비슷함 👀
그건 그렇고 발표할 생각에 눈앞이 깜깜하다😧 SOLO부터 얘기해야할꺼 같고 레퍼런스 달린 논문들도 다 언급은 해야할꺼 같은데.. 언제 다 정리한담 😥
그래도 내용은 너무 신기하다 이게 이렇게 된다고..!? 엥 ఠࡇఠ ( ꒪⌓꒪) 의 연속

생각보다 SOLO의 내용이 매우 많이 필요하므로 꼭 한번 읽고오세요 😡

---

1. Introduction

이전 SOLO: Segmenting Objects by LOcations 게시글에서 introduction에 이미 많이 적어뒀지만, segmentation 문제를 푸는 방식에는 다양한 접근 방법이 존재한다.

가장 먼저 주어진 이미지에서 RoI를 찾고 각각의 bounding box내에서 instance의 segment를 찾아내는 top-down 방식과 affinity relation을 이용해 각 픽셀의 embedding vector를 구하고, 그 vector들을 잘 묶어서 하나의 instance를 구하는 bottom-up 방식이 있다.그리고 마지막으로 이 논문에서 사용하는 raw image에서 곧바로 segment map을 찾아내는 방법이 있다.

여기에서는 기존의 SOLO 아키텍쳐에서 mask learning이라는 개념을 추가하고, NMS를 mask NMS로 수정해 더 효율적이고 빠른 SOLO2를 제안한다.

🌊 Decoupled head from SOLO

사실 저번에 SOLO 리뷰할때 decoupled head로 수정한 부분 다음 SOLO2에서 설명해야지~ 하고 넘어갔는데 뒤에서 언급하면 너무 중언부언할꺼 같아서 여기에서 간단하게 설명하고 넘어가려고 한다.

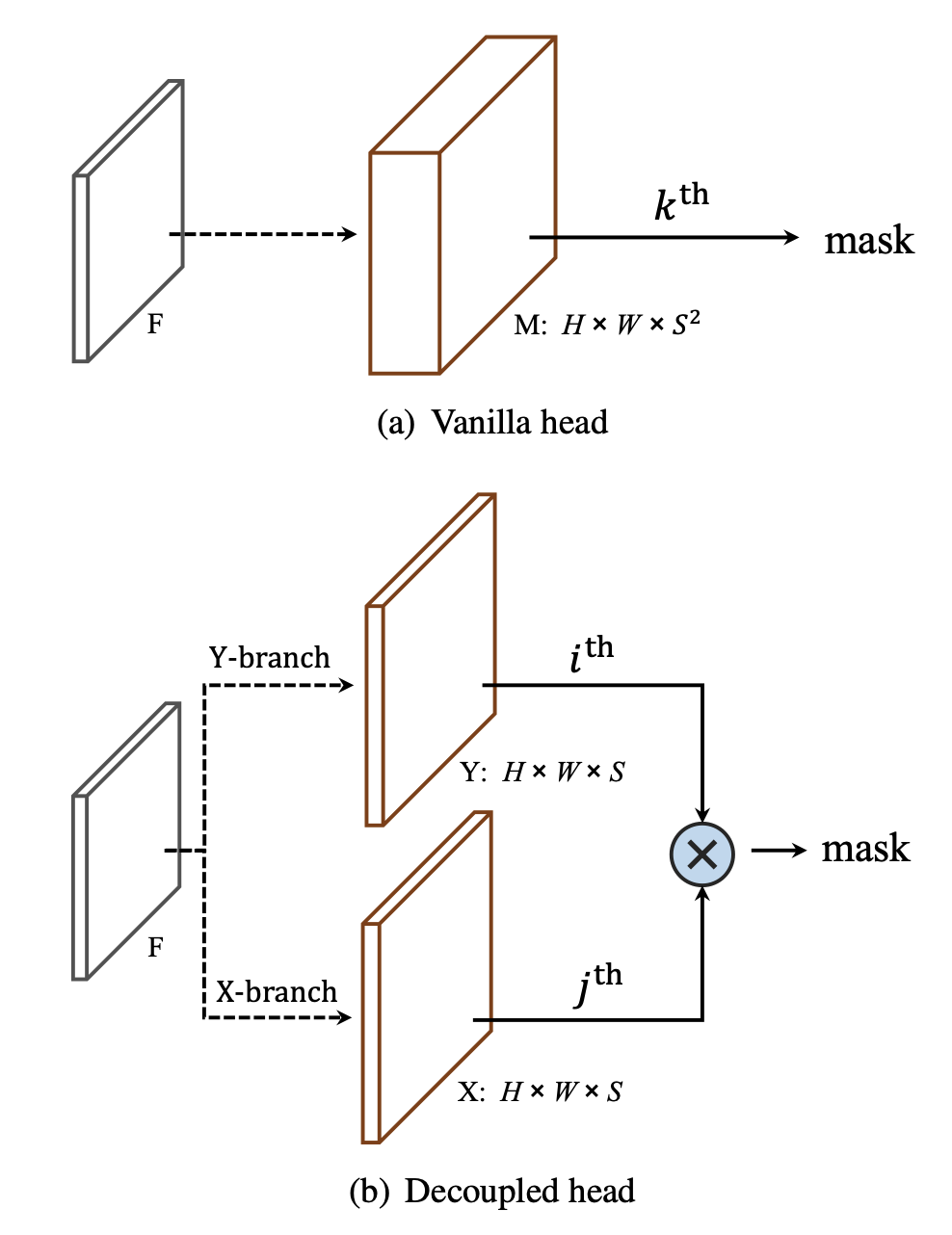
SOLO의 아키텍쳐에서 mask branch (vanilla head)쪽을 다시 가져와서 보면, feature map $F$에서 convolution 연산을 거쳐 채널축의 깊이가 $S^2$인 텐서를 만들어내는 것을 알 수 있다. 그 텐서에서 $k=i*S+j$ 번째 mask를 가져오면 $grid(i,j)$ 에 중심이 있는 object의 mask를 찾을 수 있다는게 SOLO의 주된 내용이었다.

그런데 사실 $S^2$라는 텐서의 깊이는 약간 많이 깊기는 하다.. $S$를 20으로만 잡아도 텐서의 깊이가 400이 되는데 그 중에서 대부분이 같은 object를 중복해서 잡는다던가 의미없이 아무 것도 잡지 못한다. (한 이미지에서 평균 object 수 3개) 그래서 head 부분에서 x축과 y축을 따로 예측하는 decoupled head를 제안했다. vanilla head에서 depth가 $S^2$ 였던 걸 $S$로 끌어내리고 그 대신 x축과 y축으로 나눠서 output space를 $H \times W \times 2S$로 줄였다.

이렇게 되면 이전 vanilla head에는 $i$와 $j$를 이용해 $k$를 계산하고 $k_{th}$ mask를 가져오면 됐었는데, decoupled head에서는 Y-branch에서 $i_{th}$ map을 가져오고 X-branch에서 $j_{th}$ map을 가져와 이 두 map을 element-wise로 곱해주기만 하면 된다.

decoupled head의 SOLO로 실험을 진행했을 때 기존 vailla head의 SOLO와 성능이 비슷했고, training / testing 할때 GPU 사용량은 현저히 줄어들었다.

2. SOLOv2: Dynamic, Faster, and Stronger

SOLO2에서는 SOLO에서 크게 2가지가 개선되었는데, head부분과 post-processing(NMS)이다.

Head 부분에서는 다이나믹하게 segmentation을 할 수 있도록 mask를 learning 하는 방식(convolution kernel learning and feature learning)으로 변경했다. 이렇게 되면 input 자체에 맞는 kernel을 이용해서 연산을 진행할 수 있기 때문에 훨씬 다이나믹하다.

그리고 기존의 NMS가 segmentation 연산을 하기에는 오버헤드가 크고, 병렬연산을 진행하기 힘들다는 한계를 극복한 mask NMS를 제안한다. 이 방법은 SOLO2 뿐만 아니라 다양한 object detection method들과 함께 사용해도 성능이 향상된다고 한다.

2.1 Dynamic Instance Segmentation

이전의 SOLO에서 마지막 mask branch를 생각해보면(사진 위에 있다), 가장 마지막 layer는 1X1 convolution layer로 $H \times W \times E$ 크기의 텐서를 $H \times W \times S^2$ 크기의 텐서로 바꾸어 준다. 그러면 그 마지막 layer의 kernel은 $1 \times 1 \times E \times S^2$의 크기를 가지게 될 것이다.

그렇다면, output map($H \times W \times S^2$ 크기의)을 $M$이라고 하고, 1x1 convolution layer 이전의 feature map을 $F$, convolution의 kernel을 G라고 했을 때, 마지막 연산을 $M = F * G$ 로 표현할 수 있다. 그런데 여기에서 last feature map $F$는 고정되어 있고, output $M$은 중복되는 mask가 많이 존재한다.

그렇다면 convolution kernel $G$를 그냥 바로 학습해주면 $M$이 중복되지 않고 잘 나오지 않을까?

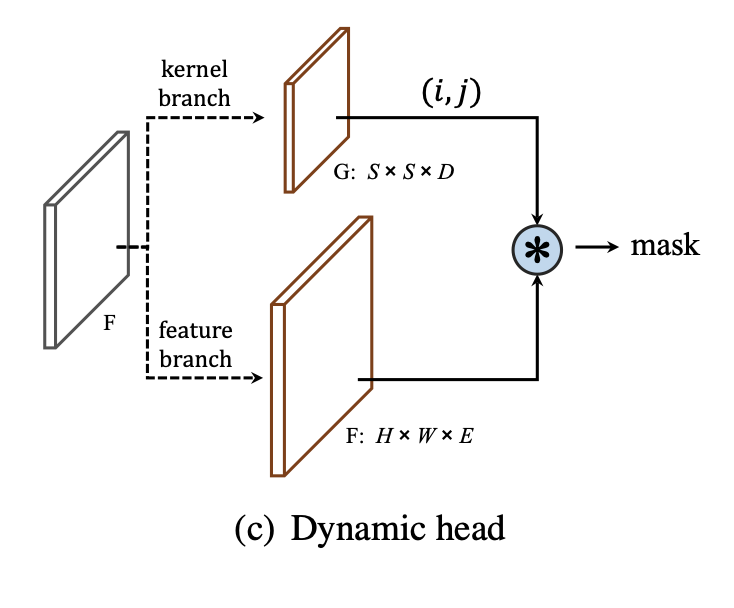
이런 고민을 해결하기 위해서, SOLO2에서는 mask prediction을 kernel learning과 feature learning으로 나누어 수행한다.

❤️ Mask Kernel Branch

Mask kernel branch는 모든 grid pixel마다 $D$차원의 output을 만들어 낸다. 위에서 설명한 것과 같이 1x1 convolution layer를 사용한다면 $D$와 $E$가 동일하겠지만, 3x3 convolution layer를 사용한다면 $D$는 $9E$와 동일하게 된다. 하나의 3x3 convolution kernel에 9개씩 값이 들어가는 걸 생각하면 될꺼 같다.

💛 Mask Feature Branch

그리고 feature branch를 생각해보자. feature branch는 좋은 feature map $F$를 예측해야한다. feature map의 크기는 $H \times W \times E$이고, 여기서 $E$는 kernel branch 설명할 때 언급했던 $E$와 같은 의미이다.

만약에 kernel branch에서 구한 모든 $S^2$개의 weight을 전부 사용해서 output mask map을 구한다면, 그 크기는 $H \times W \times S^2$가 된다. 설명이 횡설수설 하는 것 같기는 한데, 1x1을 기준으로 생각하고 tensor와 weight의 shape을 생각해보면 금방 이해가 갈 것이다..🙄

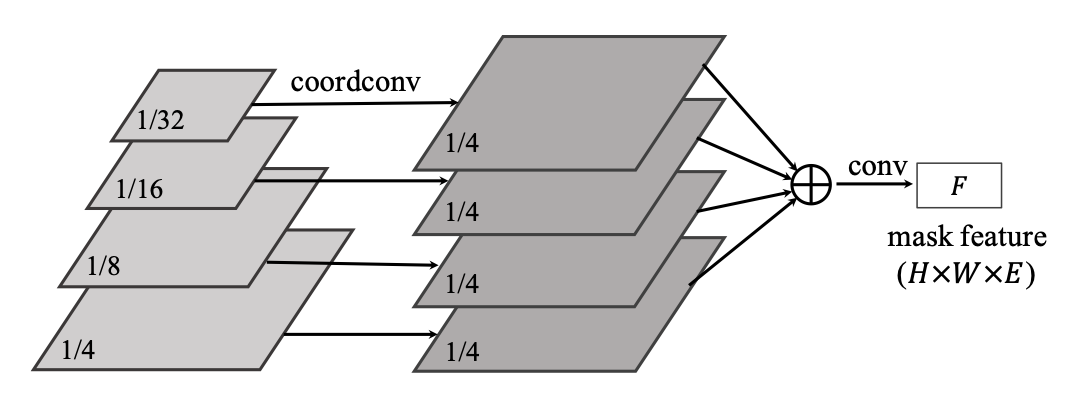
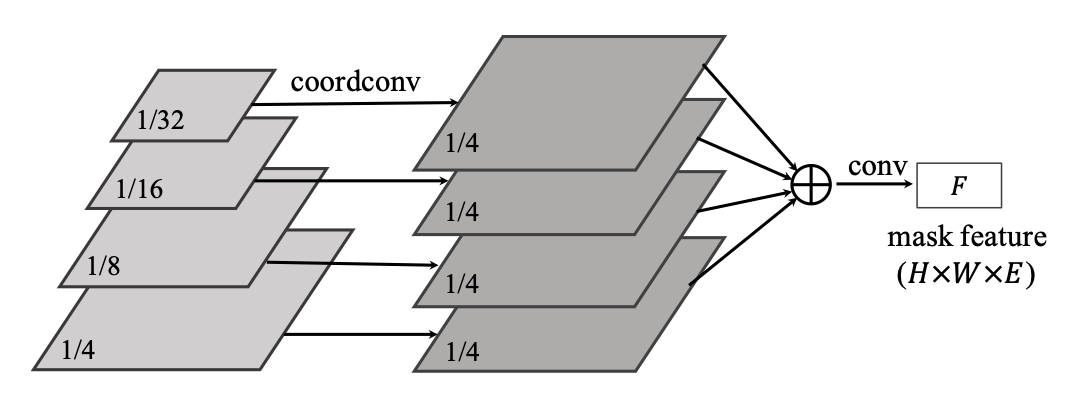
그런데 방금 설명한 dynamic head는 FPN의 모든 feature pyramid level마다 달려 있어야 한다. feature map의 크기가 다르다 보니 어떻게 보면 당연한 소리일 수도 있는데, 바로 위의 사진 처럼 하나의 resolution으로 맞춰서 하나의 $F$를 만들어 head를 하나만 달아주는 방법도 있다. FPN에서 나온 다양한 resolution의 feature를 1/4의 크기가 될때까지 upsampling 해주고, 크기가 맞춰진 모든 feature를 element-wise로 더해주고 1x1 convolution을 거쳐 unified mask feature $F$를 만들었다고 한다.

제일 작은 resolution인 1/32의 경우에는 직접적으로 x, y 좌표를 알려주는 CoordConv를 사용해서 위치정보를 알려줬다고는 하지만.. 이게 사실 어떻게 기존 아키텍쳐보다 성능이 더 좋게 나왔는지는 잘 이해가 안된다. 다양한 resolution의 feature map을 서로 합침으로써 rich semantic information을 가지면서도 local 정보도 가지고 있는 그런 feature map을 얻을 수 있게 된건가..😩 아직 Panoptic Feature Pyramid Network를 안 읽어봐서 감 못 잡는 것 같아서 이 논문을 읽어보고 unified feature branch를 다시 이해해봐야겠다..

(20.07.06 추가) Panoptic Feature Pyramid Network paper를 궁금해서 읽고 왔는데, 저 resolution 들을 합쳐서 conv를 씌워 pixel-wise prediction을 찾는 걸 하나의 독립된 branch로 생각한다.
여기에서는 좋은 $F$를 찾기 위해서 branch 하나를 팠다고 생각해도 될 것 같다. 각 level별로 구하는 것보다 이렇게 summation을 이용하는게 더 효율적이고 robust하다고 한다.

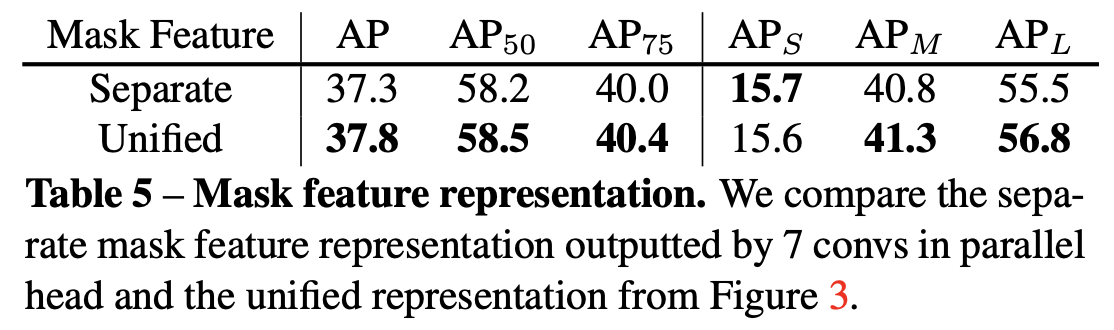
이 table은 Unified architecture가 더 성능이 좋다는 실험 결과이다.

💚 Learning and Inference

Loss function은 이전 SOLO에서 사용한 loss식과 동일하다. $L_{category}$를 conventional focal loss라고 하고 $L_{mask}$를 mask prediction의 loss라고 할 때, loss $L$은

이거 식도 그렇고 웬만한거는 다 SOLO와 같으니까 그 부분을 확인하면 좋을 것 같다.

2.2 Matrix NMS

SOLOv2에서 새롭게 제안하는 Matrix NMS은 soft NMS에서 영감을 받아서 만들었다고 한다. 사실 NMS 알고리즘들을 많이 공부해보지는 않아서 이 부분은 내가 잘못 이해했을 수도 있다 😅

💙 Explanation

Soft NMS는 두 object의 iou가 높으면 더 낮은 object를 제거하는게 아니라 detection score를 단순감소함수 $f(iou)$만큼 곱해줘서 천천히 감소시킨다. Soft NMS와 관련해서는 나중에 글을 따로 써서 올릴 예정이니까 여기에서는 자세하게 설명은 하지 않겠다.

기존의 soft NMS에서는 단순히 decay factor를 단순감소함수 $f(iou)$를 이용해서만 정의했다. 하지만 matrix NMS에서는 두가지를 기준으로 decay factor를 정한다. $m_i$와 $m_j$ 두 mask 중 $m_i$의 점수가 더 높을 때, $m_j$의 decay factor는

1. $m_i$가 $m_j$에게 주는 패널티 → $f(iou_{i,j})$
2. $m_i$가 suppressed될 확률 → IoU 가지고 추정

이 두가지를 가지고 정의할 수 있다. 사실 suppress될 확률을 곧바로 구하는건 좀 어려우니까 suppress될 확률과 IoU가 양의 상관관계에 있다고 생각하고 추정(다른 mask와의 iou가 높을 수록 suppress될 확률 높음)해서 사용한다.

(+ 처음 읽을 때 헷갈렸던 건데 $f(iou_{i,j})$ 는 IoU 값을 의미하지 않는다. 아래에서 다시 정의할 예정)

이렇게 하면 $m_i$가 가장 많이 겹친 mask와의 IoU를 기반으로 $m_i$가 suppress될 확률을 근사적으로 구할 수 있다.

decay factor에 영향을 주는 값을 2개 다 구했으니 $decay_j$ 를 구하면 다음과 같다.

이러한 과정을 거쳐 나온 decay factor $decay_j$를 이용해 $s_j = s_j\cdot decay_j$를 계산하고 업데이트 한다.

$f(iou_{i,j})$는 lienar function과 gaussian 두가지로 정의할 수 있다.

• [linear] $f(iou_{i,j}) = 1 - iou_{i,j}$
• [gaussian] $f(iou_{i,j}) = exp(-\frac{iou_{i,j}^2}{\sigma})$

🖤 Implementation

NMS를 계산하는 수도 코드이다 🤨
matrix를 구하고 pairwise IoU를 구해서, 순서대로 decay factor를 구하고 있으니까 코드+논문을 읽어보면 금방 이해할 수 있을 것이다 👩‍💻

def matrix_nms(scores, masks, method=’gauss’, sigma=0.5): 
# scores: mask scores in descending order (N)
# masks: binary masks (NxHxW)
# method: ’linear’ or ’gauss’
# sigma: std in gaussian method

# reshape for computation: Nx(HW)
masks = masks.reshape(N, HxW)

# pre−compute the IoU matrix: NxN 
intersection = mm(masks, masks.T)
areas = masks.sum(dim=1).expand(N, N)
union = areas + areas.T − intersection
ious = (intersection / union).triu(diagonal=1)

# max IoU for each: NxN
ious_cmax = ious.max(0)
ious_cmax = ious_cmax.expand(N, N).T 
# Matrix NMS, Eqn.(4): NxN
if method == ’gauss’: # gaussian
	decay = exp(−(iousˆ2 − ious_cmaxˆ2) / sigma) else: # linear
	decay = (1 − ious) / (1 − ious_cmax) 
# decay factor: N
decay = decay.min(dim=0)
return scores ∗ decay

3. Experiments

Mask learning과 mask NMS를 이용한 SOLOv2로 실험을 진행했을 때 특히 큰 object에서 기존의 실험결과보다 더 좋은 결과를 얻었다고 한다.

그리고 mask feature branch의 output을 visualization을 했을 때 두가지 양상을 발견할 수 있었다.

위의 사진에서 주황색? 살구색?으로 체크되어 있는 feature map은 position-aware 해서 왼쪽에서 수평으로 image를 스캔한 것과 같은 output임을 확인할 수 있고, 흰색으로 체크되어 있는 feature map은 foreground에 있는 모든 object를 하이라이트하고 있다.

이건 개인적으로 SOLOv2가 생각보다 boundary detail을 잘 찾아서 신기해서 가져온 figure이다.

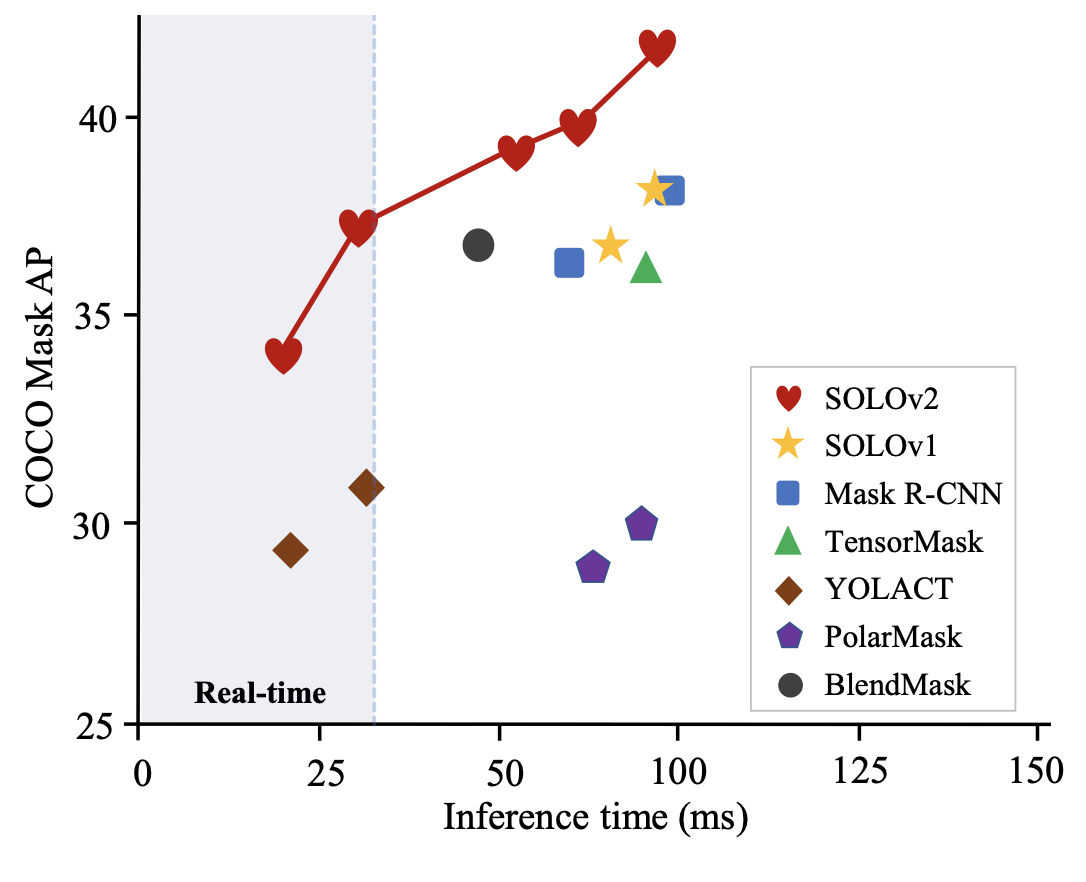
SOLOv2의 압도적인 성능을 보여주는 귀염뽀짝 그래프이다.. 하트가 정말 너무 인상적인 피겨.. inference time 보고 놀랬는데 Tesla V100-GPU에서 실험 돌렸다고 해서 내가 실험 돌려보지는 못하겠구나 하고 빠른 포기를 했다 😇

얼마나 Matrix NMS가 효율적인지를 알 수 있는 table이다. 기존 NMS들과 비교했을 때 시간과 성능 모두 뒤지지 않는다.

4. Conclusion

이 논문에서는 기존 SOLO: Segmenting Objects by Location 에서 head와 NMS를 수정한 SOLOv2를 제안한다. 기존 연구에 비해 더 빠르고 정확한 모델을 소개하면서, 다른 instance level task에서도 충분히 활용될 수 있는 dynamic kernel과 기존의 NMS 대신 쉽게 붙일 수 있는 빠르고 효율적인 matrix NMS를 제안한다.

(+ 이거 하나 읽으려고 지금 레퍼런스 한 5개는 읽은 것 같다😱 읽은거 언제 하나하나 정리한담)
(+ 읽는데 하루 글 쓰는데 이틀 걸렸다🥱 저주받은 집중력)

reference

• https://arxiv.org/abs/2003.10152