Linear Regression

from sklearn import datasets

boston = datasets.load_boston()
X =  boston.data
y = boston.target

print(X.shape)
print(boston.feature_names)

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)

from sklearn.linear_model import LinearRegression
from sklearn.tree import DecisionTreeRegressor
model = LinearRegression()
model.fit(X_train, y_train)

print(model.coef_)   #회귀식의 계수. y=ax + bx2 + ... 
print(model.intercept_)   #절편 

model.score(X_test, y_test) # R-square(r2_score)   #사이킷런 분류문제 스코어 원칙 정확도 

y_pred = model.predict(X_test)

#분석결과 시각화
plt.scatter(y_test, y_pred, edgecolors=(0, 0, 0))
plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'k--', lw=4)
plt.xlabel('Measured')
plt.ylabel('Predicted')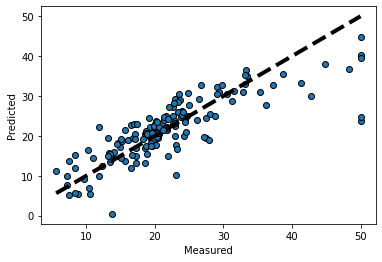

선형회귀 분석

다중공선성 제거

1. 상관계수 기반

corr_matrix = X.corr()

#상관계수 행렬에서 feature 쌍과 상관 계수를 추출 
correlation_pairs =[]
for col in corr_matrix_columns:
	for index, value in corr_matrix[col].nlargest(n=2).iteritems():
    	if index != col:
        	correlation_pairs.append((col, index, value))
            
# 상관계수가 높은 순서대로 feature 쌍 추출 
cor_col, cor_idx, cor_val =[], [], []
for pair in sorted(correlation_paris, key=lambda x: abs(x[2]), reverse=True):
	cor_col.append(pair[0])
    cor_idx.append(pair[1])
    cor_val.append(pair[2])

result_corr = pd.DataFrame({'col1': cor_col, 'col2': cor_idx, 'corr_val': cor_val})

corr_07 = result_corr.loc[result_corr['corr_val'] > 0.7]
cols_07 = pd.concat([corr_07.col1, corr_07.col2], ignore_index=True)
cols07_valcnt = cols_07.value_counts().sort_values(ascending=False)
del_cols = cols07_valcnt[cols07_valcnt.values > 1].index
#len(del_cols)
X.drop(columns = del_cols, inplace=True)

2. VIF 기반

import statsmodels.api as sm
from statsmodels.stats.outliers_influence import variance_inflation_factor

X_ = sm.add_constant(X)
model = sm.OLS(y, X_)
result = model.fit()

vif_df = pd.DataFrame()
vif_df['Variable'] = X_.columns
vif_df['VIF'] = [variance_inflation_factor(X_.values, i) for i in range(X_.shape[1])]
vif_df.sort_values(by='VIF, ascending=False)

sel_features = vif_df.loc[vif_df['VIF'] <5, 'Variable'][1:].tolist()  # 상수항 제외 
X = X[sel_features]

p-value 확인

import statsmodels.api as sm
X_ = sm.add_constant(X)
result = sm.OLS(y, X_).fit()

p_values = result.pvalues
p_values_df = pd.DataFrame({'Featrues': X_.columns, 'p-value': p_values})
sel_features = p_values_df.loc[p_values_df['p-value'] < 0.05].index.values.tolist()   # p-values 만족하지 않는 변수 제외 
sel_features.remove('const')

X_sel = X[sel_features]

OLS 적합 후 선형회귀 가정 만족 확인

model = sm.OLS(y, sm.add_constant(X_sel))
result = model.fit()
result.summary()

잔차그래프 확인

residuals = result.resid

plt.scatter(result.fittedvalues, resuiduals)
plt.xlabel('Fitted Values')
plt.ylabel('Residuals')
plt.title('Residual Plot')
plt.show()

영향점 확인

import statsmodels.stats.outliers_influence import OLSInfluence

inf = OLSInfluence(result)
inf.plot_index('cook', thereshold = 4/(result.nobs - X_sel.shape[1] -1)) # cook's distance, threshold 기준은 thumb of rule, threshold 이상인 경우에 plot에 index 표시 
plt.show()

# 영향점 제거 후 다시 적합
X_sel2= X_sel.drop(index = inf_idx)
y2 = y.drop(index = inf_idx)

results2 = sm.OLS(y2, sm.add_constant(X_sel2)).fit()
results2.summary()

OLS Regression Results 해석

• Durbin-Watson 통계량

  오차항의 상관성: 오차항(잔차)이 서로 상관되어 있지 않다는 가정

  $D = \frac{\sum_t (e_t-e_{t-1})^2}{\sum_t e_t^2} \approx 2(1-r)$

  • $r$: sample autocorrelation
  • $0<D<4$
  • $D \approx 2$ : no autocorrelation
  • $D \approx 0$ : positive serial correlation(잔차간의 양의 상관이 높다)
  • $D \approx 4$: negative serial correlation

• Prob(JB)

  오차항(잔차)은 정규분포를 따른다는 가정

  • Jarque-Bera 검정은 잔차의 정규성을 평가하기 위해 사용됨
  • 'Prob(JB)' 값이 작을수록 (일반적으로 0.05보다 작으면) 잔차가 정규 분포를 따르지 않을 가능성이 높다

선형회귀 모델 적용

from sklearn.linear_model import ElasticNetCV
from sklearn.linear_model import ElasticNet

from sklearn.model_selection import KFold
from sklearn.metrics import mean_squared_error
from sklearn.metrics import r2_score

elastic_cv = ElasticNetCV(cv=5, random_state=42)
elastic_cv.fit(X, y)
# 최적의 매개변수(alpha, l1_ratio) 출력 

kf = KFold(n_splits = 5, shuffle=True, random_state=0)

model = ElasticNet(alpha = 0.01, l1_ratio=elatic_cv.l1_ratio_, random_state=42)
mse_sum = 0
r2_sum =0
for tr_idx, val_idx in kf.split(X, y):
	tr_x, tr_y = X.iloc[tr_idx], y.iloc[tr_idx]
    val_x, val_y = X.iloc[val_idx], y.iloc[val_idx]
    
    model.fit(tr_x, tr_y)
    pred = model.predict(val_x) 
    
    mse = mean_squared_error(val_y, pred)
    mse_sum += mse 
    
    r2 = r2_score(val_y, pred)
    r2_sum += r2
    
print(f'Elastic Net - mse: {mse_sum/5}, r2: {r2_sum/5}')