PCA
Baisic PCA
from sklearn.decomposition import PCA
pca = PCA(n_components=x.shape[1], whiten=False)
# 이미 정규화가 되어있기때문에 whiten False
# x.shape[1]은 열개수 =784. 축소 안한다?
pca.fit(x)
x_pca = pca.transform(x) # 하지만 결과는 기존 데이터와 똑같지는 않다.
### 주성분에 의해 설명되는 비율
sum(pca.explained_variance_ratio_) #99.99%
comp = [10, 20, 50, 100, 200]
for c in comp:
v = sum(pca.explained_variance_ratio_[:c])
#print('%3d개 주성분 : %.4f' % (c, v))
print(f'{c}개 주성분 :{v:.4f}')
# 10개 주성분 :0.4971
# 20개 주성분 :0.6533
# 50개 주성분 :0.8316
# 100개 주성분 :0.9184
# 200개 주성분 :0.9683
### 숫자 분류에 영향을 주는 두 특성으로 산점도 시각화
RFC = RandomForestClassifier(max_depth=10, n_jobs=-1)
RFC.fit(x, y)
pca_xy = np.where((-RFC.feature_importances_).argsort()<=1)[0]
# minus -> 가장 큰 숫자부터 index 출력
# argsort 결과가 0이라는 것은 가장 작은 숫자라는 의미, 즉 여기서는 가장 큰 숫자
# <=1 이므로 0번째, 1번째 index를 출력해준다.
pca_xy
# 633번, 687번 변수가 가장 중요한 변수이다. Incremental PCA
- 미니배치로 PCA 수행, 미니배치 적용때마다 점진적으로 PCA성능 개선
- 레코드가 충분하면 Basic PCA와 거의 유사하나 메모리 사용량이 낮음
Sparse PCA
- sparse는 자료해석의 용이함, 과대적합 방지 등에 효과가 있음
- alpha값이 클수록(희소성의 유지가 잘 될수록) 일부 입력 변수에서만(0을 무시하고) 선형 결합 탐색
- 일반 PCA보다 계산량이 많아 데이터가 커질수록 속도가 저하됨
Kernel PCA
- 원본 데이터 쌍들에 대해 유사성을 개선하여 비선형적으로 차원을 축소
- 비선형 결합 방식은 RBF(주로 사용), sigmoid, cosine 등이 있음
- RBF(Radial Basis Function)에서는 gamma가 커질수록 비선형 정도가 강해짐
- 데이터에 noise, 이상치가 많은 경우에 사용
SVD
- Singular Value Decomposition
- ML에서는 PCA보다 SVD가 더 잘 요약하는 편이다
Random Projection
- 점 사이 거리의 배열이 유지되도록 저차원으로 점을 투영
- (직관적) 원래 데이터가 KxN 행렬이면 여기에 임의의 NxM 행렬을 곱해서 KxM행렬로 바꾼다. N차원이 M차원이 된다.
- 일반버전 : GRP(Gaussian Random Projection)
- 희소버전 : SRP(Sparse Random Projection)
- 일반적으로 속도 GRP > SRP
Nonlinear Dimensional Reduction
매니폴드 학습
: 두 점 사이의 거리가 근거리에서는 유클리디안 직선 거리 이지만 원거리에서는 그렇지 않은 공간 -> 바르고 곧은 유클리디안 공간을 탐색
Isomap
- Isomap은 fit_transform이 존재하지 않음
- metrics(거리측정방법) : default - minkowski
t-SNE
- t-SNE는 다른 차원축소 기술을 사용해 줄인 차원을 이용할때 더 효과적
- 왜곡이 심함. 가까운 것은 더 가깝게 먼 것은 더 멀게.
- 그림만 그려보는 용도로 많이 쓰임
from sklearn.manifold import TSNE
tSNE = TSNE(n_components=2, learning_rate=300)
x_tSNE = tSNE.fit_transform(x_SVD)ICA(Independent Component Analysis)
- 특성들에는 함께 포함된 수많은 독립적인 신호가 존재
- 혼합성을 개별 성분으로 분리 -> 일부 조합을 추가해 원래 피처를 재구성
(e.g. 음악에서 보컬만 분리)
from sklearn.decomposition import FastICA
ICA = FastICA(n_components=25, whiten=True)
x_ICA = ICA.fit_transform(x)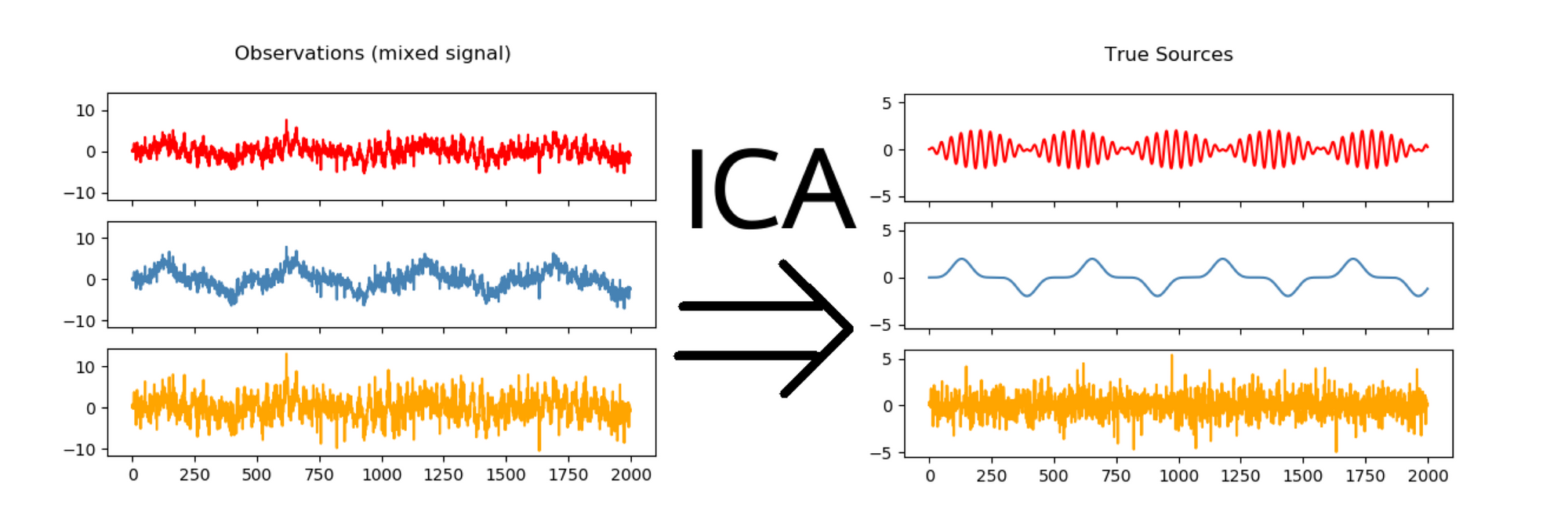
.jpg)