그리디란?
자판기는 남은 금액을 어떤 알고리즘을 반환할까? 그리고 마시멜로 실험에서 마시멜로가 하나 있고 30분을 참으면 마시멜로를 하나 더 준다고 가정할 때 아이들은 어떤 선택을 하는 것인가를 테스트 하는 실험이다.
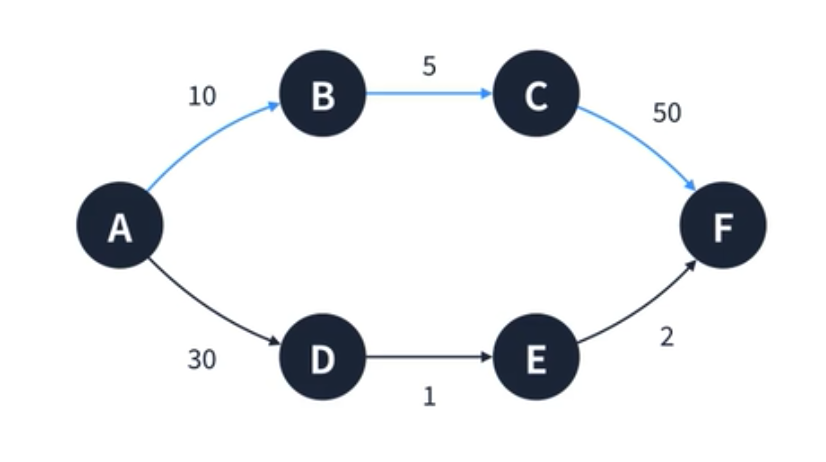
그리디 알고리즘은 매 선택에서 지금 이순간 최적인 답만을 선택하는 알고리즘이다. 최적해를 보장해주지 않는다. 아래의 그림을 보면 먼저 A 부터 갈수 있는 정점은 B와 D가 있다. A가 볼 때는 B가 더 짧기 때문에 B를 선택한다.
이어서 C, F 로 이동하여 총 이동 거리는 65 가 된다. 하지만 실제 최적해는 D를 선택했을 때이다. D를 선택하면 총 이동거리가 33이 된다.
그리디 알고리즘의 특징
- 보통 최적해를 구하는 알고리즘보다 훨씬 빠른 경우가 많다. 특징상 되게 선형 시간만에 끝나는 경우가 많다.
- 크루스칼, 다익스트라 알고리즘 등에 사용된다.
- 직관적인 문제 풀이에 적합하다.
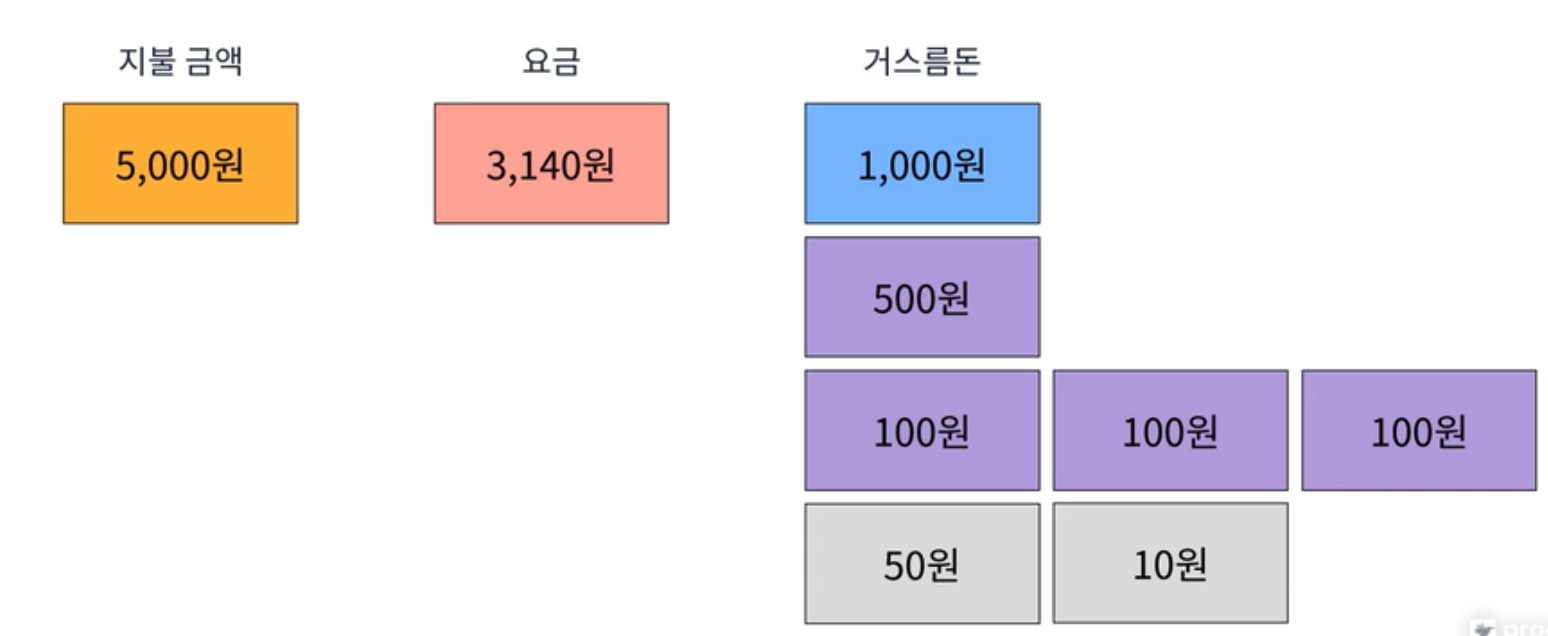
위의 자판기 반환 문제를 어떻게 해결하면 좋을까? 지불 금액은 5000원, 요금은 3140원일 때 거스름 돈은 1860원이다. 여기서 편의를 위해 거스름돈은 큰 단위부터 거슬러 줘야 할 때 어떻게 해야 할까?
답은 매우 간단하다. 거스름돈 1860원을 가장 큰 단위부터 처리하면 된다. 먼저 1000원 반환이 가능하기 때문에 거스름돈에서 1000원을 뺀다. 나머지 860원에서 1000원을 거슬러 줄 수 없기 때문에 다음으로 큰 단위인 500원을 반환한다. 그럼 남은 거스름돈은 360원이 된다. 다음으로 큰 단위인 100원을 세번 반환하면 남은 거스름돈은 60원이 된다. 이런 방식으로 각각 50원과 10원을 반환하면 최대한 적은 횟수로 거스름돈을 줄 수 있게 된다.
그리디 문제 풀이
그리디 알고리즘은 대게 동전 반환 문제와 같이 진행되는 경우가 많다. 참고로 여기서 착각하면 안되는 점은 그리디는 특정 구현 방법이 존재하는 것이 아닌 하나의 개념으로 봐야 한다는 점이다. 따라서 그리디 알고리즘은 문제를 풀면서 이해하는 것이 가장 좋다.