BFS, DFS
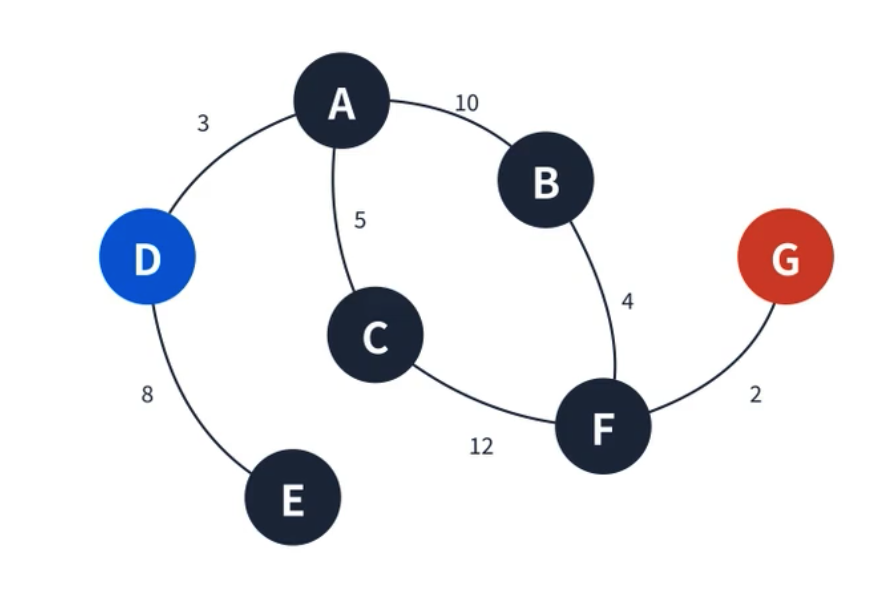
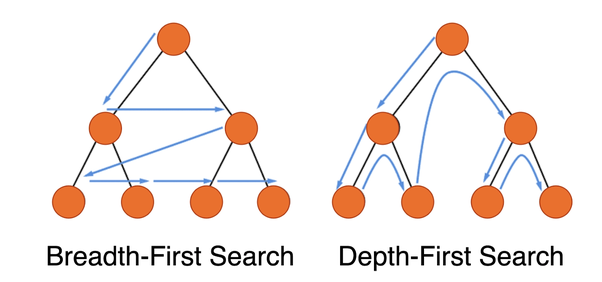
이 알고리즘은 각각 넓이 우선 탐색(Breadth-First-Search)과 깊이 우선 탐색(Depth-First-Search)이라고 부른다. 그림판의 페인트 툴은 어떻게 구현 될까? 그리고 만약 D에서 G로 가는 최단 거리는 어떻게 알 수 있을까? 넓이 우선 탐색과 깊이 우선 탐색을 이용하면 구현할 수 있다.
너비 우선 탐색(BFS)
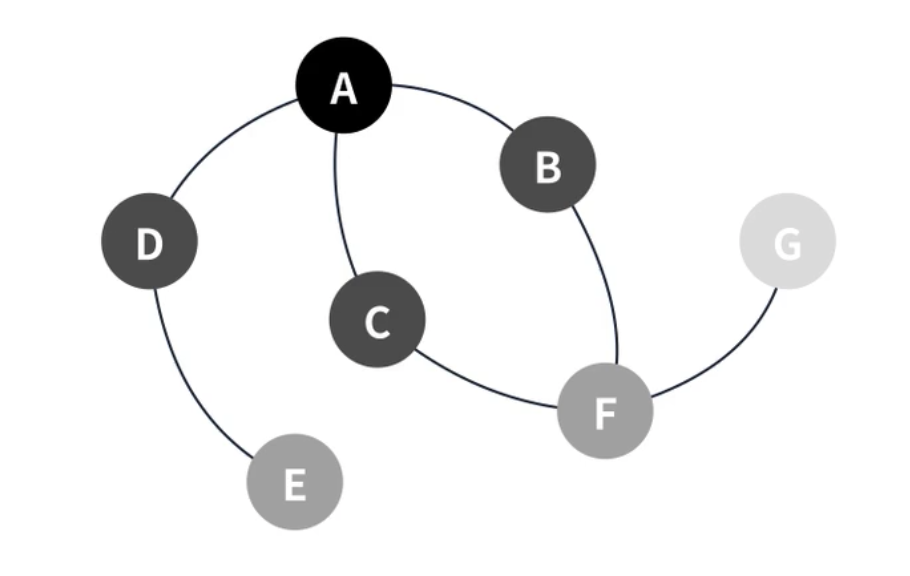
그래프 탐색 알고리즘 중 하나로 같은 깊이에 해당하는 정점부터 탐색해나가는 알고리즘이다. 아래의 그림 예시를 보면 A 부터 시작하여 점점 퍼져나가도록 시각화 하였다. 먼저 A를 탐색하고 이어서 B, C, D 를 탐색한 후 그 다음 단계인 E, F 마지막으로 G를 탐색한 것으로 표현한 것이다.
BFS 의 특징
- Queue 를 이용하여 구현할 수 있다.
- 시작 지점에서 가까운 정점부터 탐색한다.
- V 가 정점의 수, E 가 간선의 수일 때 BFS 의 시간복잡도는 O(V + E)다.
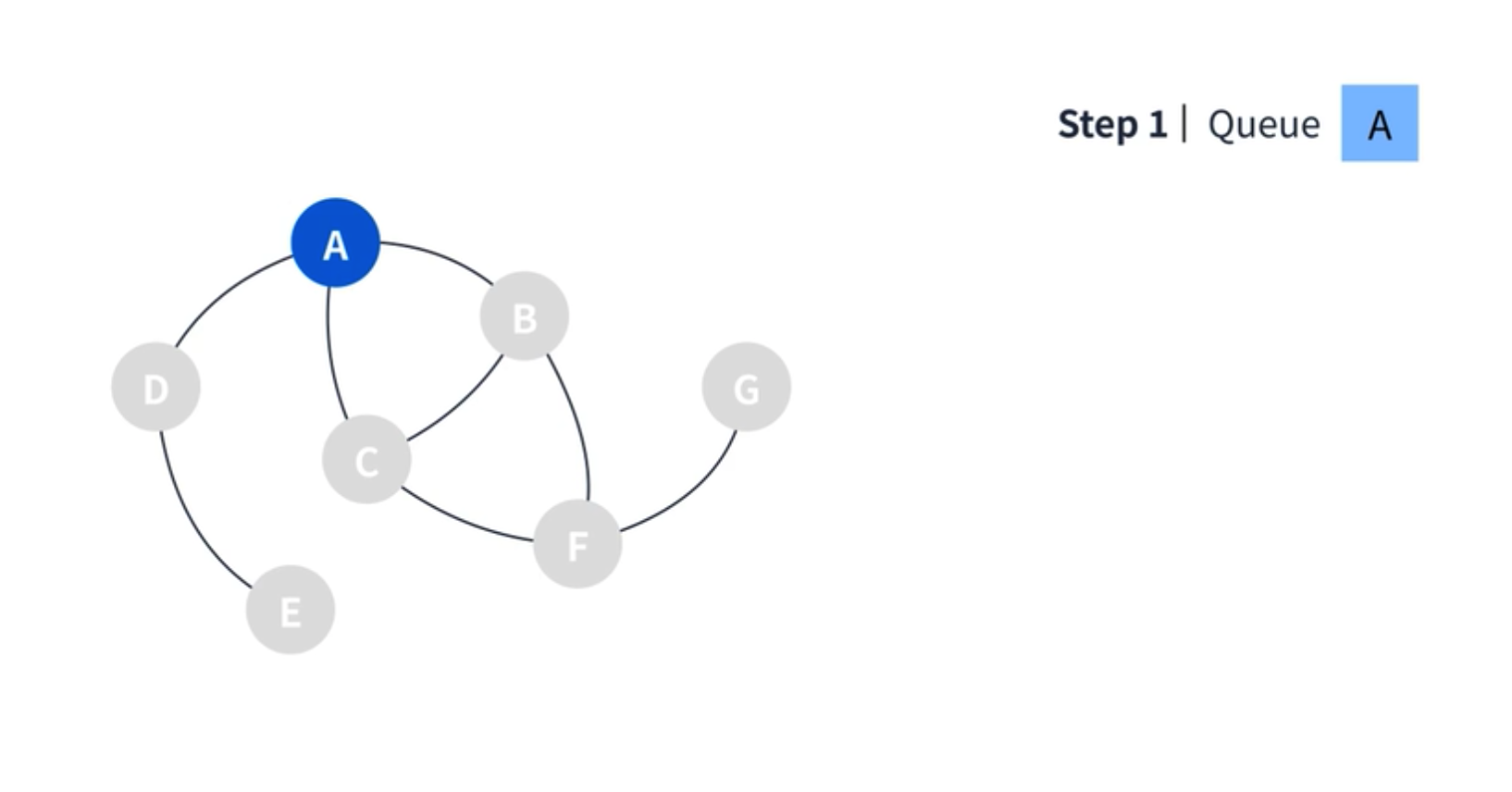
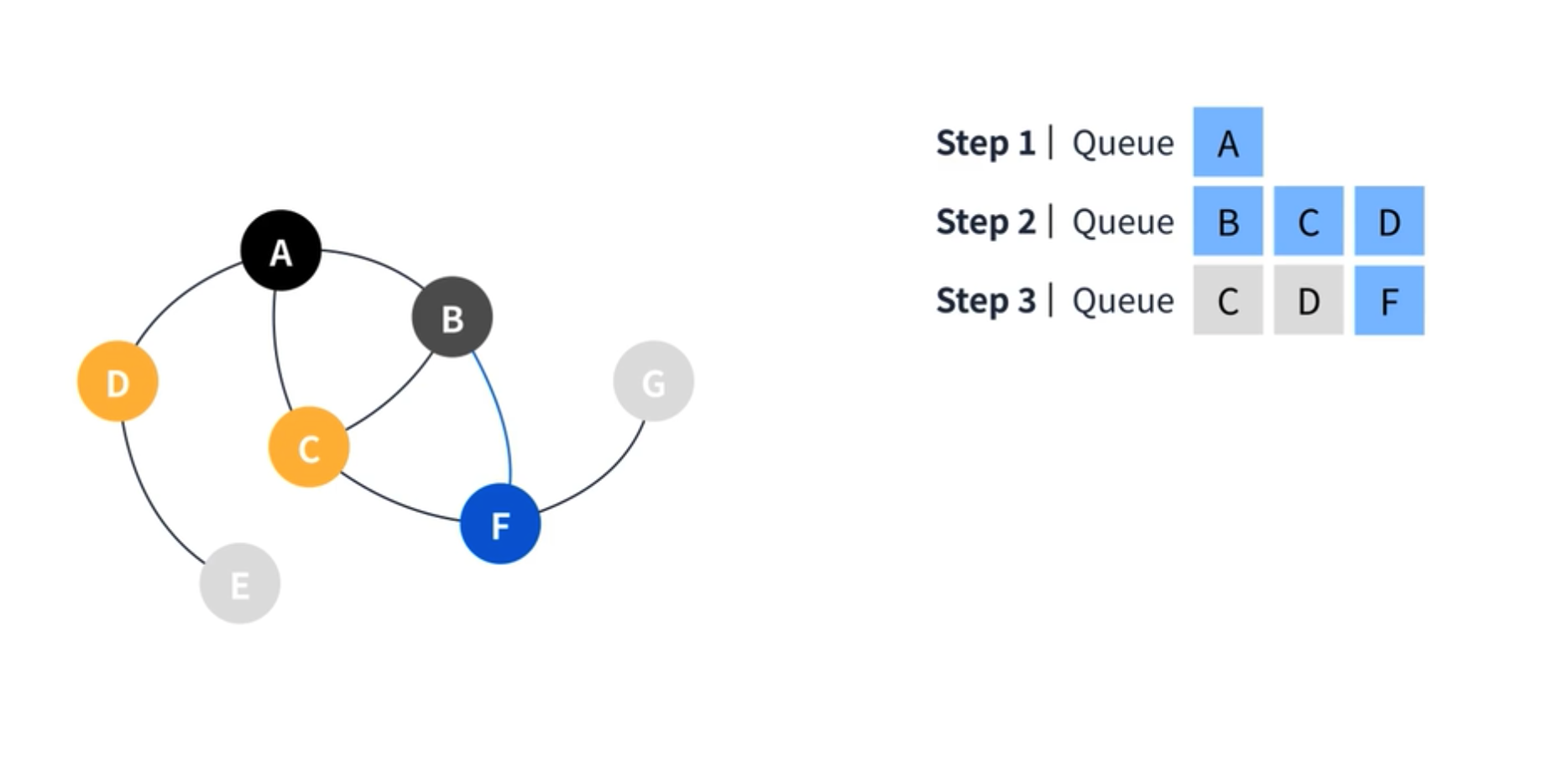
동작 순서는 아래와 같다. 먼저 시작 지점을 A 라고 가정할 때, 큐에 A 를 넣는다.
큐에 있던 A 를 디큐(Dequeue)하고 A 로부터 이동할 수 있는 간선의 수를 체크하여 해당 정점들을 모두 큐에 넣는다. 다음은 B 정점을 디큐하여 B 로 부터 이동 가능한 정점을 큐에 넣는다. 이때 C는 이미 방문한 곳이기 때문에 추가 하지 않는다.
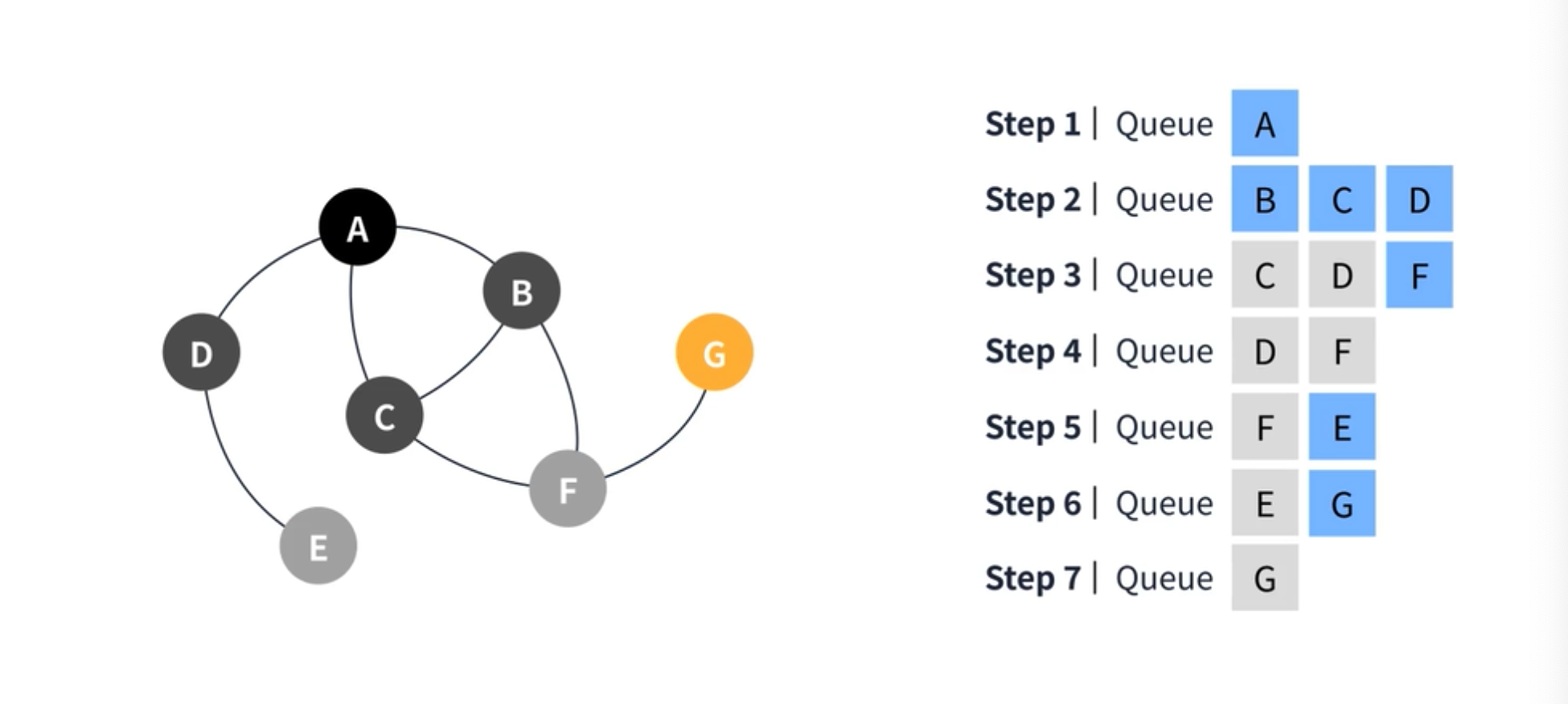
다음은 C 정점을 디큐한다. C 정점에선 F로 갈 수는 있지만 이미 큐에 추가가 되었기 때문에 아무것도 하지 않고 종료한다. 다음으로 D 를 디큐한 후 D 와 연결된 E 정점을 큐에 추가한다. 다음으로 F 정점을 디큐한 후에 F 와 연결된 G 정점을 추가한다. E 정점은 더 이상 갈 수 있는 정점이 없기 때문에 디큐만 하고 종료한다. 마찬가지로 G 정점도 더 이상 갈 수 있는 정점이 없기 때문에 그대로 종료된다. 보시다시피 BFS 는 시작 지점에서 인접한 요소부터 탐색하며 진행된다.
깊이 우선 탐색(DFS)
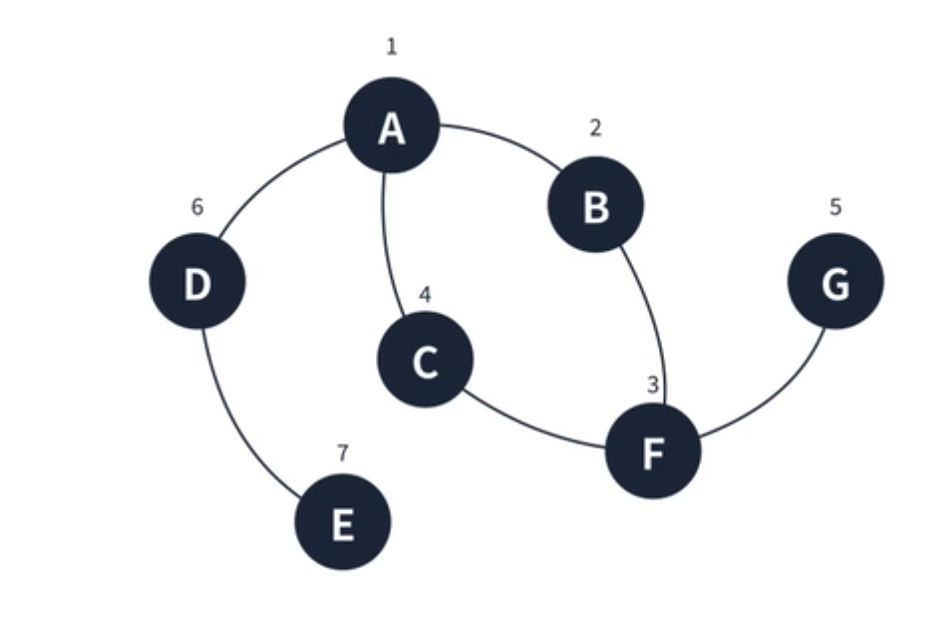
그래프 탐색 알고리즘 중 하나로 최대한 깊은 정점부터 탐색하는 알고리즘이다. 예시를 살펴보면 아래와 같다. 탐색 우선 순위가 더 작은 알파벳이 우선이라 가정할 때, 아래의 그림을 보면 A 정점부터 시작하여 B, F, C 로 이동한 것을 볼 수 있다. C 에서 더 이상 방문할 곳이 없어 F에서 G 로 이동한다. G에선 더 이상 이동할 간선이 없기 때문에 그대로 다시 A까지 빠진다. 이어서 D 를 탐색하고 E 를 탐색하면 깊이 우선 탐색이 마무리된다.
DFS 의 특징
- Stack 자료구조를 이용하여 구현 할 수 있다.
- 시작 정점에서 깊은 것 부터 찾는다.
- V 가 정점의 수, E 가 간선의 수일 때 BFS 의 시간 복잡도는 O(V+E)다.
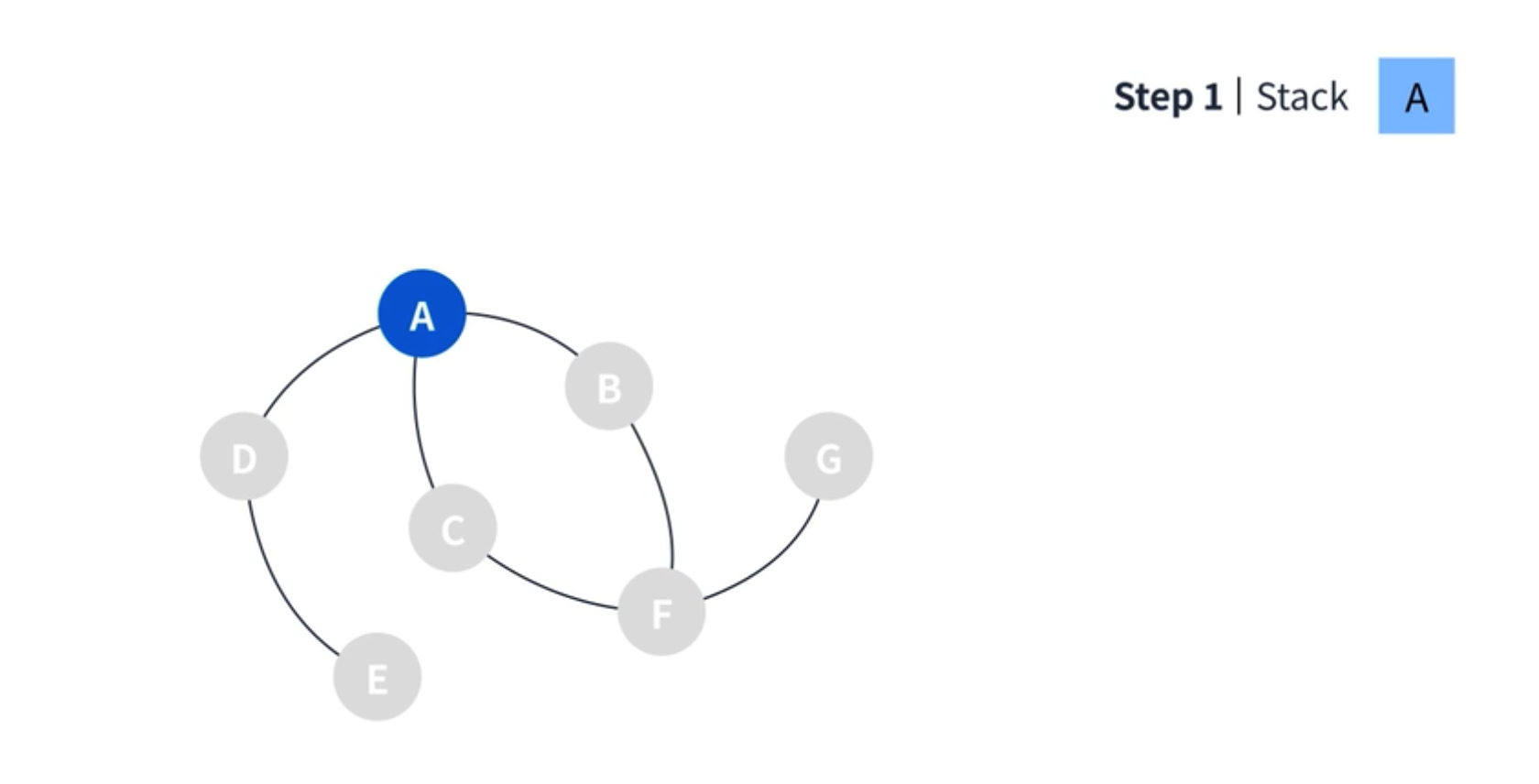
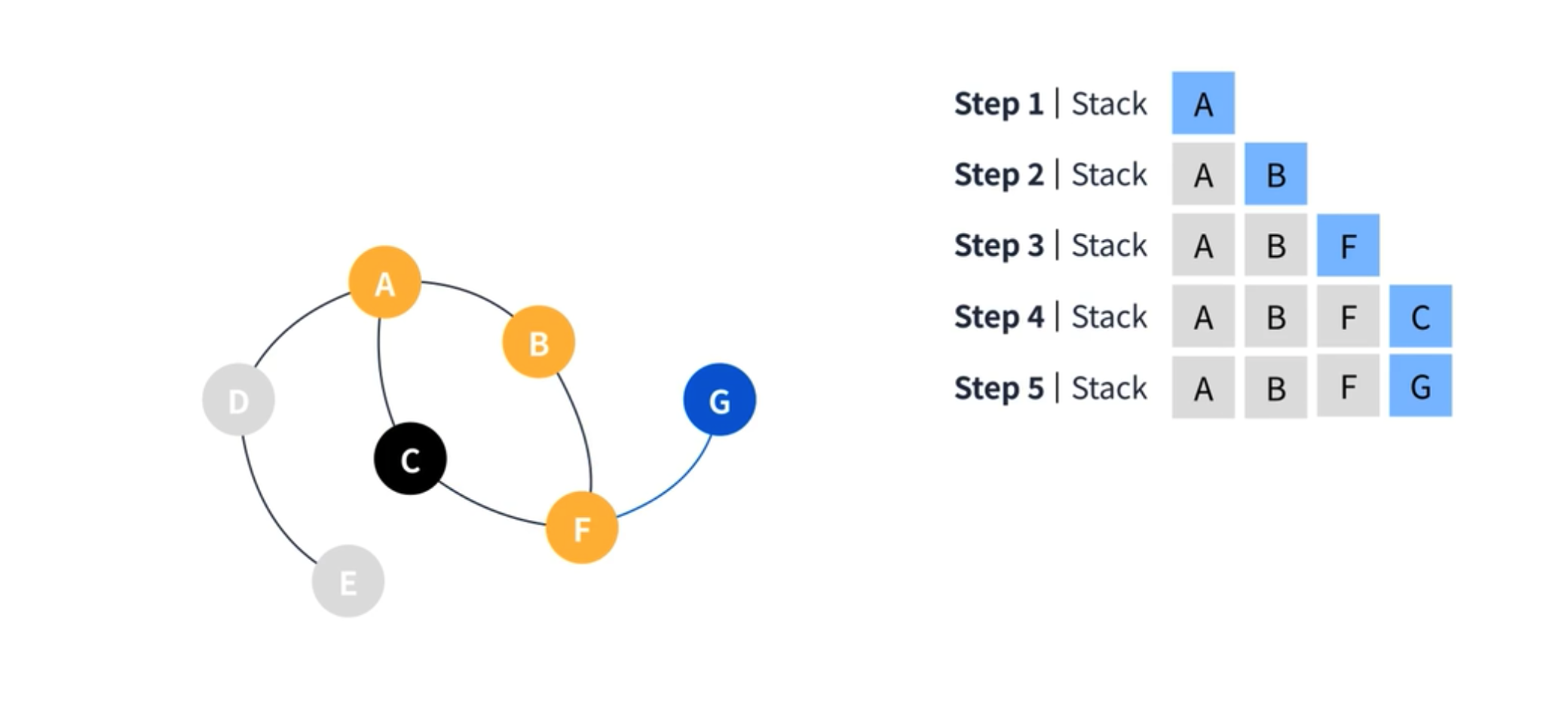
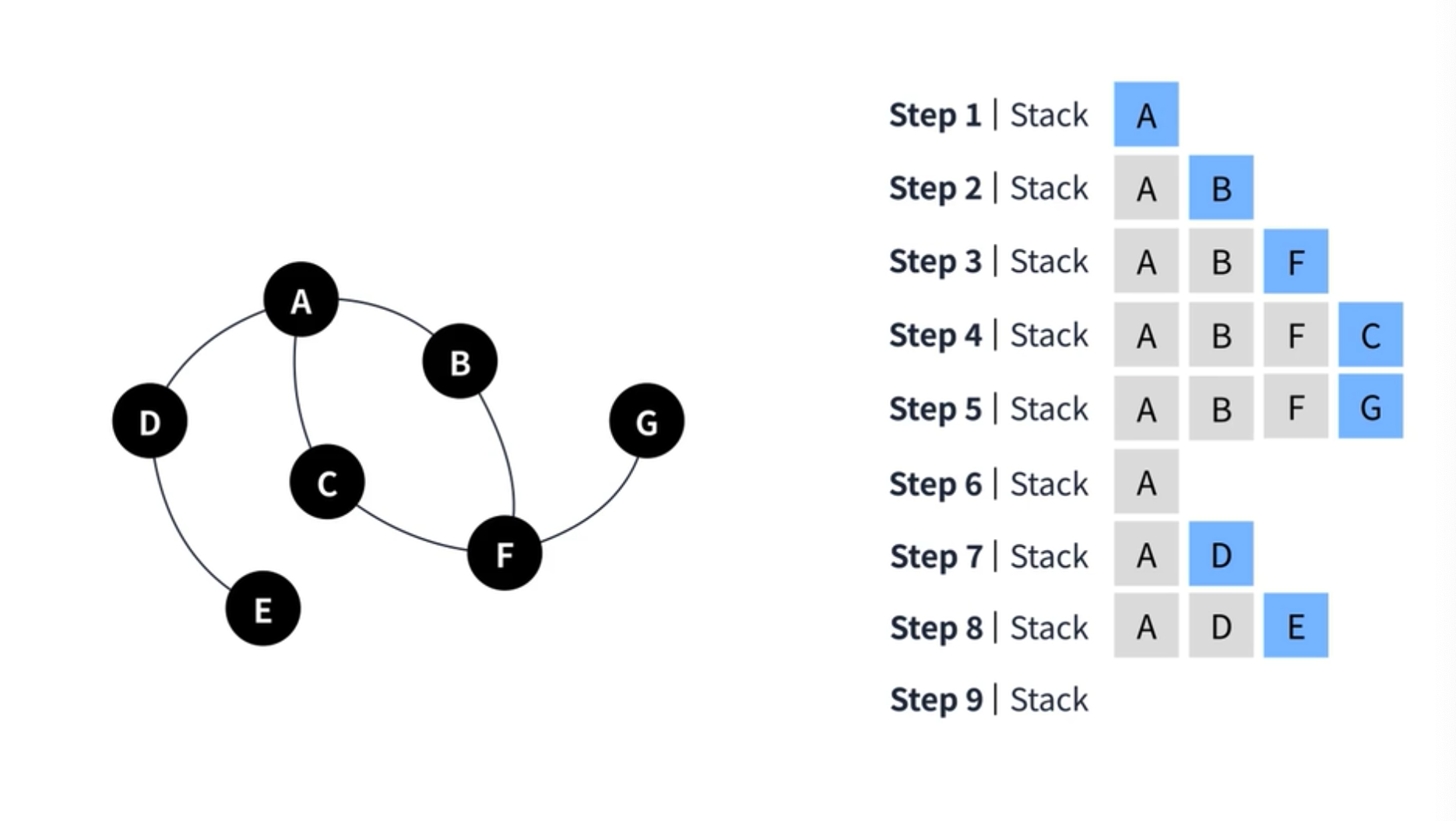
동작 순서는 아래와 같다. 이번에도 A부터 시작할 것이기 때문에 스택에 A를 넣는다.
스택의 탑인 A 를 참고하여 이동할 수 있는 정점인 B 를 스택에 추가한다. 이어서 스택의 탑인 B 에서 이동할 수 있는 정점인 F 를 추가한다. 또 이어서 스택의 탑인 F 에서 갈 수 있는 정점인 C 를 스택에 추가한다.
C 에서는 더 이상 갈 수 있는 곳이 없기 때문에 Pop 하고 다시 F 에서 갈 수 있는 정점인 G 를 스택에 추가한다. G 에서는 더 이상 갈 수 있는 곳이 없기 때문에 그대로 Pop 한다. 나머지 F 와 B 도 더 이상 갈 수 있는 곳이 없어 스택은 A 까지 모든 요소가 Pop 된다. 다시 A 부터 시작되어 D 를 스택에 추가한다. 이이서 E 를 추가한다. 그리고 E 에서 더 이상 갈 수 있는 곳이 없기 때문에 모든 정점을 스택에서 Pop 하게 된다.
이런식으로 DFS 는 깊은 정점부터 탐색하게 된다.