트라이란?
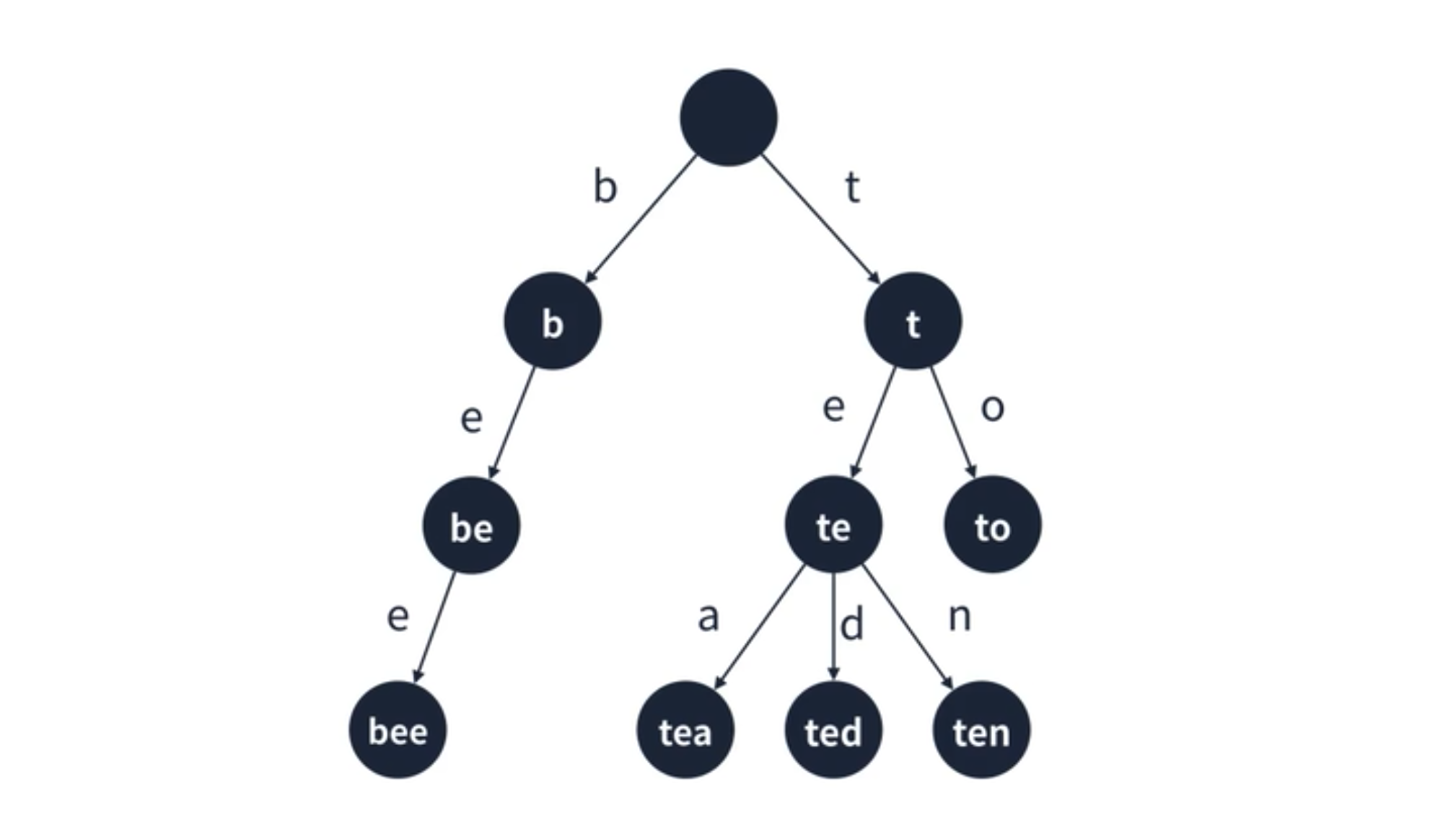
구글이나 네이버 같은 검색 서비스에서 자동 완성을 하려면 어떻게 해야 할까? 이런 경우에 사용하는 적합한 자료구조로 트라이가 있다. 트라이는 문자열을 저장하고 효율적으로 탐색하기 위한 트리 형태의 자료구조이다. 아래의 그림처럼 트리 구조로 되어 있어 간선은 이전 정점으로부터 새롭게 추가되는 문자 정보를 가지고 있다. 그리고 정점은 이전 정점으로부터 더해진 문자열 정보를 가지고 있다. 예를 들어 루트의 오른쪽 정점 t 하위는 모두 앞 글자로 t 를 가지고 있다. 이런 식으로 우리가 미리 정의한 문자열로 자동 완성을 구현할 수 있다.
트라이의 특징
- 검색어 자동완성, 사전 찾기 등에 응용될 수 있다.
- 문자열을 탐색할 때 단순하게 비교하는 것보다 효율적으로 찾을 수 있다.
- L이 문자열의 길이일 때 탐색, 삽입은 O(L)만큼 걸린다.
- 각 정점이 자식에 대한 링크를 전부 가지고 있기에 저장 공간을 더 많이 사용한다.
트라이의 생성
트라이 구조는 몇가지 규칙이 있다.
- 먼저 루트는 비어있는 공백이다.
- 각 간선(링크)은 추가돌 문자를 키로 가진다.
- 각 정점은 이전 정점의 값 + 간선의 키를 값으로 가진다.
- 해시 테이블과 연결 리스트를 이용하여 구현할 수 있다.
예시를 살펴보자.
처음에는 빈 루트 정점만 존재한다.
여기에 cat 이라는 문자열을 추가한다. 먼저 문자열의 맨 앞 ‘c’ 를 잘라 루트 정점의 자식으로 추가한다. 이어서 맨 앞 문자열 ‘a’ 를 잘라 c 정점의 자식으로 추가한다. 이때 간선의 키는 a 가 된다.
마지막 문자열 ’t’ 를 잘라 ca 정점의 자식으로 추가한다. 이렇게 되면 문자열 ‘cat’ 는 트라이 구조에 저장된다.
이번에는 문자열 ‘can’ 을 추가해보자. 맨 앞 문자열 ‘c’ 을 자른 후 확인한다. 이미 정점이 있기에 이동만 한다.
다음으로 맨 앞 문자열 ‘a’ 를 자른 후 확인한다. 이미 정점이 있기에 이동만 한다. 마지막으로 남은 문자열 ’n’ 을 자른 후 확인한다. n 간선은 없기에 정점에 추가한다.
이렇게 하면 문자열 ‘can’ 은 트라이에 저장된다.
자바스크립트에서 사용법
트라이의 로직을 구성하는 방법은 다음과 같다.
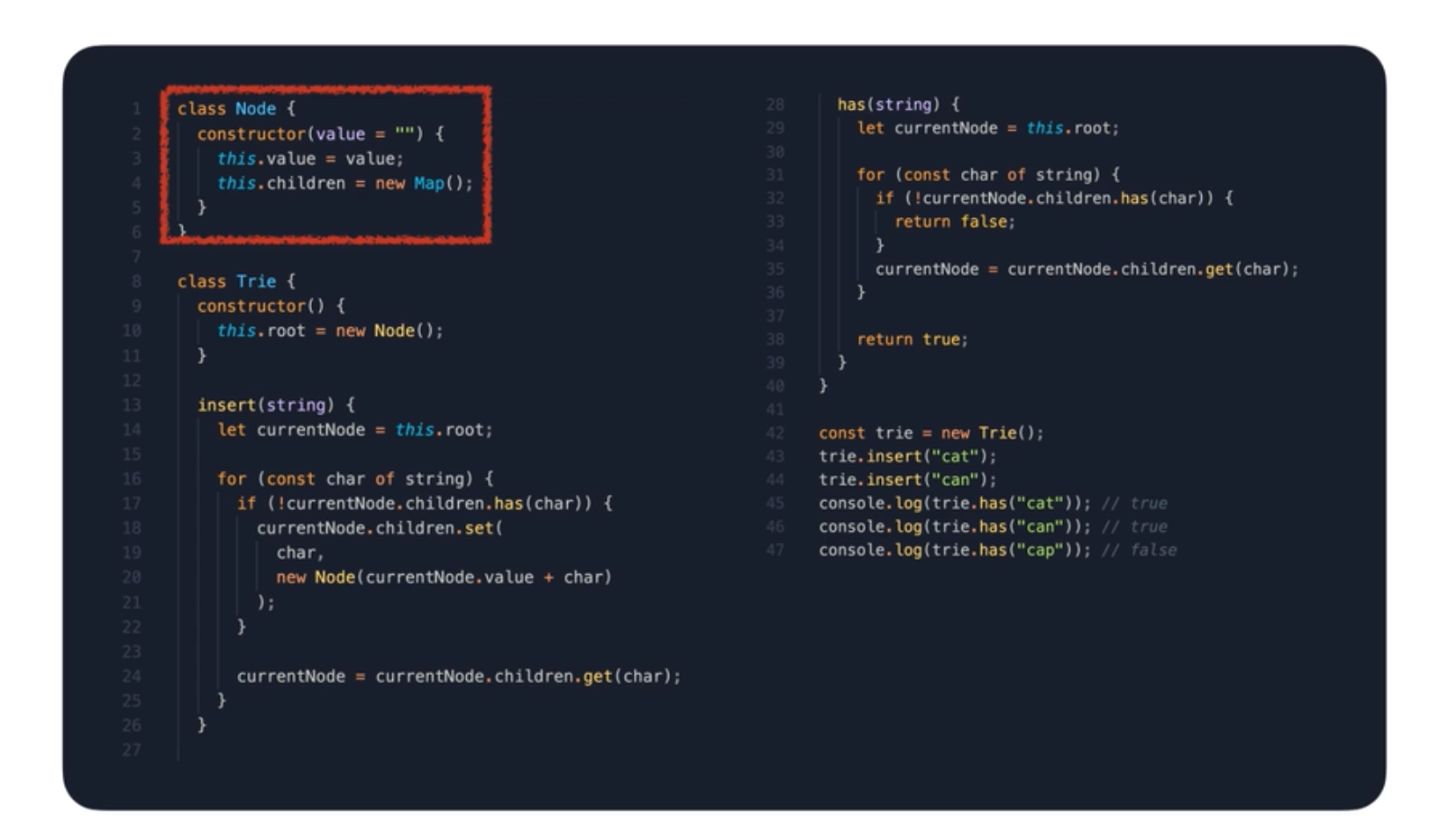
먼저 트리 구조인 만큼 그래프처럼 노드가 필요하다. 여기서 인접 리스트 형태로 구현한다. 트라이를 생성하면 root 로 빈 노드를 생성한다. 문자열을 추가하면 탐색을 위해서 루트부터 시작을 한다. 문자열을 앞에서부터 하나씩 자르면서 순회한다. 만약 현재 노드에서 짜른 문자열을 간선으로 가지고 있지 않다면, 새롭게 노드를 추가한다. 그리고 나서 다음 정점으로 이동한다. 이 루프를 반복하면 문자열을 요소로 전부 추가할 수 있다.
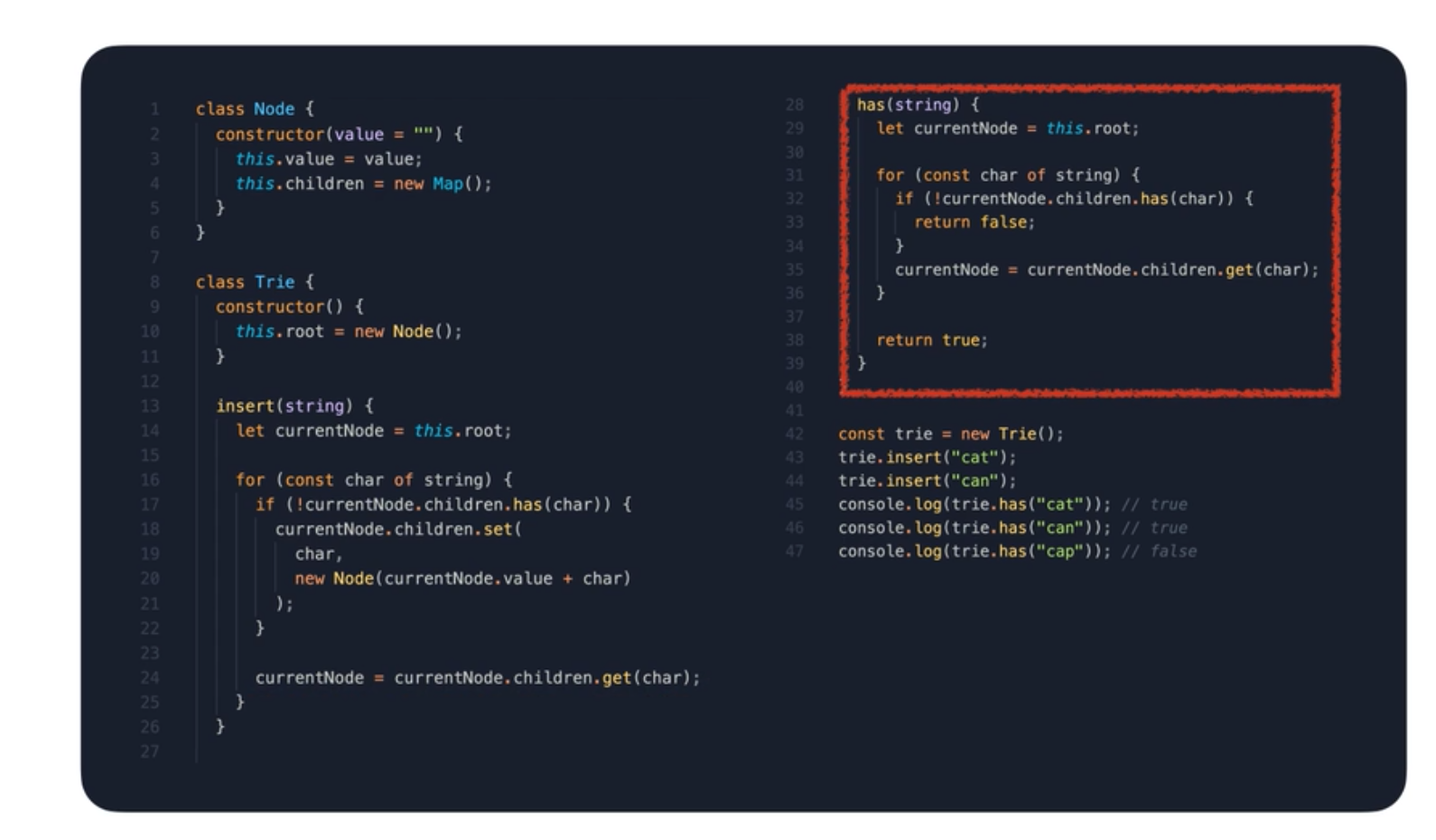
그리고 트라이에서 문자열이 존재하는지에 대한 여부를 체크하는 함수는 has 이다. 추가를 응용한 코드라서 그다지 어렵지는 않다.