이진 탐색이란?
정리가 안된 책장에서 원하는 책을 찾을려면 어떻게 하면 좋을까? 사람마다 다르겠지만 어느 방향이든 순차적으로 찾는 사람이 많을 것이다.
이러한 탐색을 선형 탐색이라고 부른다. 순서대로 하나씩 찾는 탐색 알고리즘이기 때문에 O(n) 시간복잡도가 걸린다.
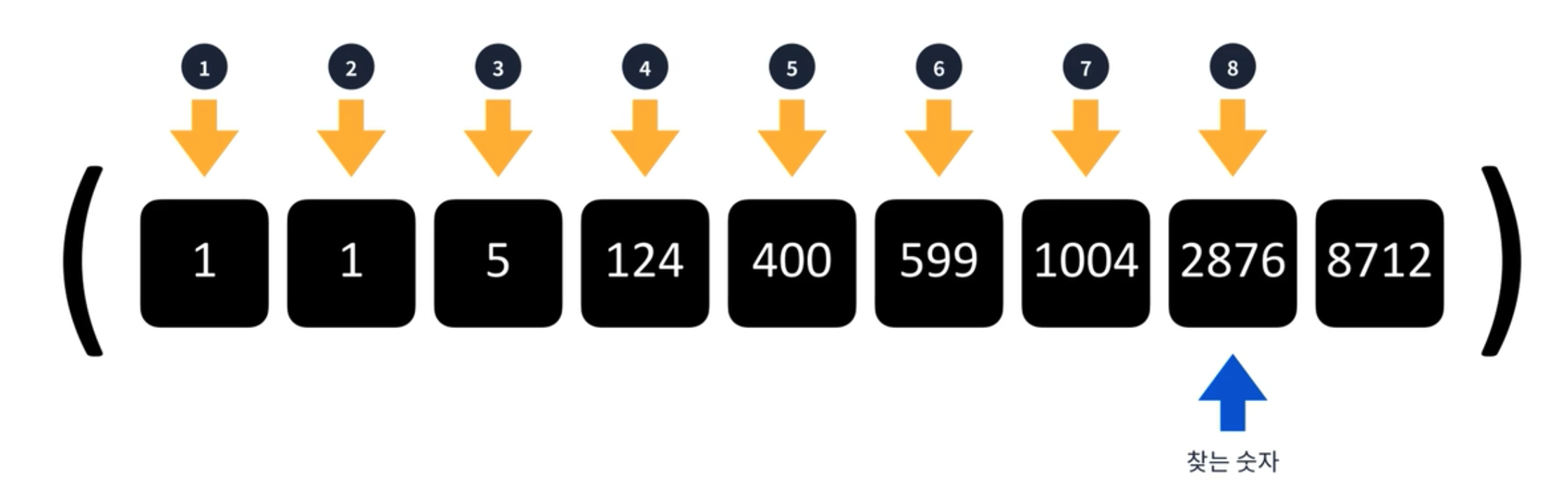
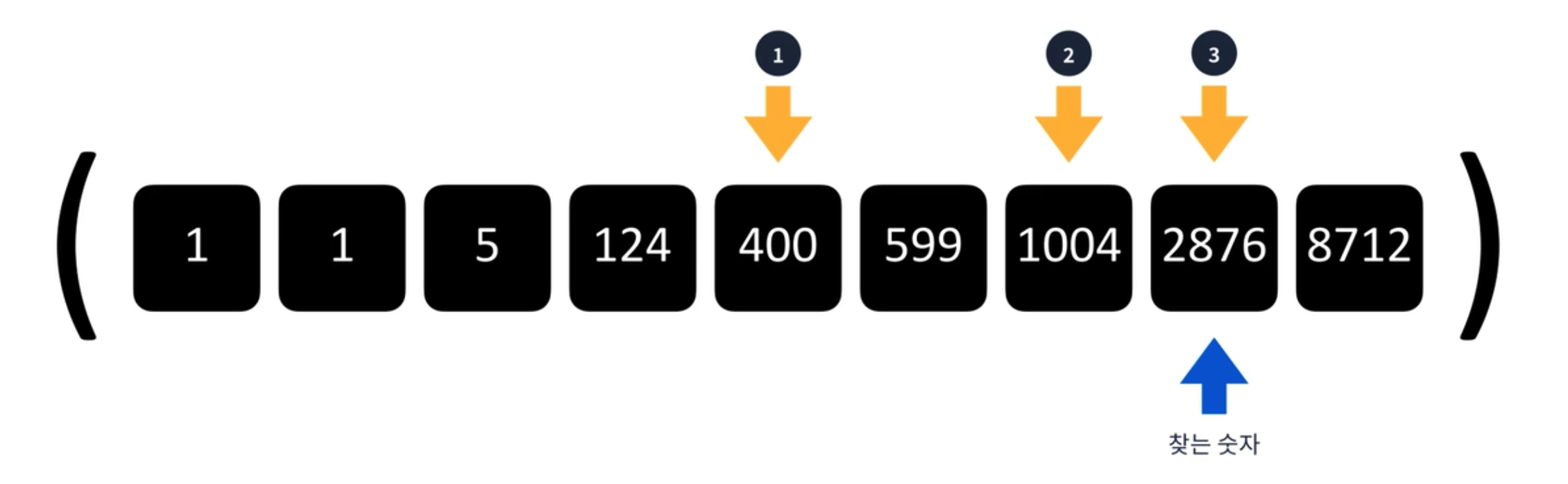
그리고 up and down 게임에 대해서 아는가? 흔히 나이 맞추기 게임을 할 때 많이 사용하는 게임이다. 예상 나이를 말하고 더 큰지 더 작은지를 판단하여 절반씩 줄여나가는 전략을 많이 사용한다.
이런 전략을 이용한 탐색을 이진 탐색이라고 부른다. 이진 탐색은 요소들이 이미 정렬이 되어야 사용할 수 있는 알고리즘이다. 즉, 정렬 되어있는 요소들을 반씩 제외하며 타겟 요소를 찾는 알고리즘이므로 O(log n)만큼 시간복잡도가 걸린다.
이진 탐색의 특징
- 반드시 정렬이 되어 있어야 사용할 수 있다. 따라서 정렬로 탐색하면 선형 탐색보다 느릴 수 있다.
- 배열 혹은 이진 트리를 이용하여 구현할 수 있다.
- O(log n) 시간복잡도인 만큼 상당히 빠르다. 정렬이 되어 있다면 가급적 이진 탐색을 이용하는 것이 좋다. 이렇게 빠른 알고리즘은 거의 없다.
배열을 이용한 구현 방법
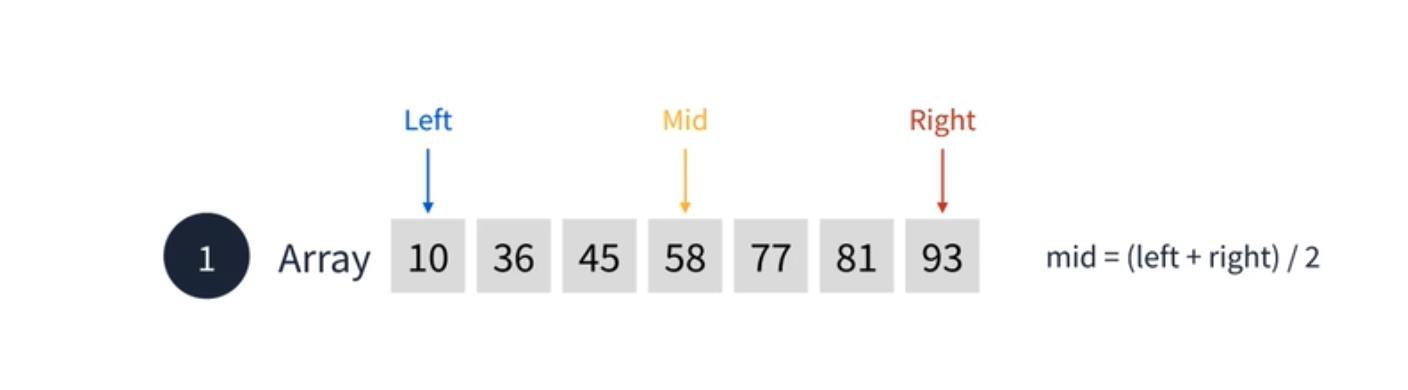
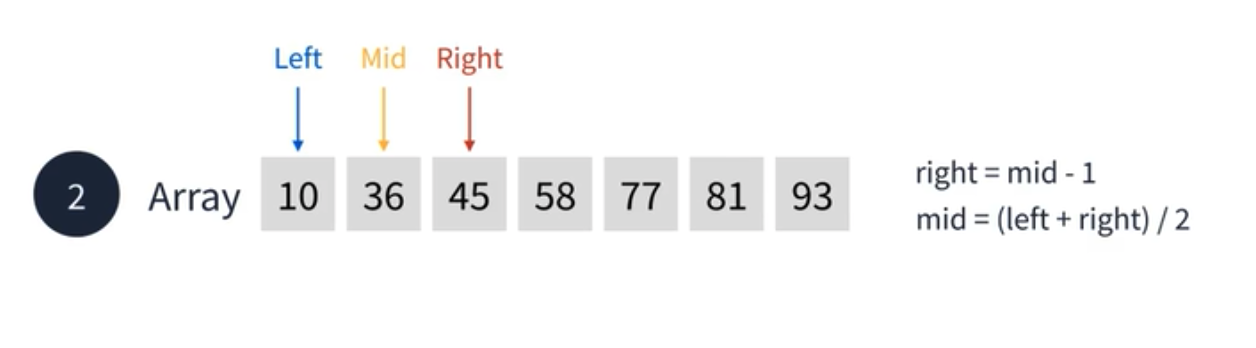
아래의 배열에서 45를 찾으려면 어떻게 하면 될까? 이진 탐색에서는 먼저 시작 지점을 Left 로 두고 끝 지점을 Right 로 둔다. 그리고 중간 지점을 Mid 라고 표현한다.
여기서 mid 와 찾을 값인 45와 비교한다. 58 보다 45 가 작기 때문에 right 값을 한칸 왼쪽에 위치한 후 다시 Mid 값을 구한다.
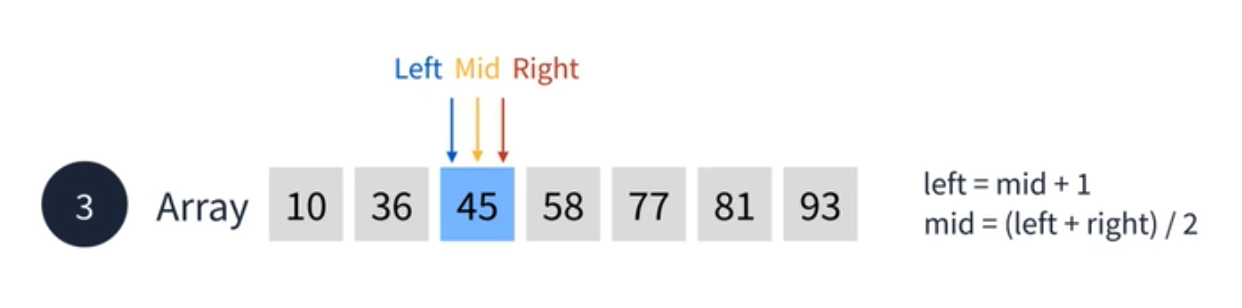
이번엔 36이 45보다 작기 때문에 Left가 36에 오른쪽으로 이동한다. 마침 Left 와 right 가 동일하기 때문에 Mid 도 동일한 값으로 다시 부여된다. 이번엔 Mid 값과 찾을 45 값이 같기 때문에 탐색이 종료된다.
배열을 이용한 방법은 중간에 요소를 추가하거나 삭제하는 경우에는 선형 시간이 걸린다는 단점을 여전히 들고 있다. 그래서 이 방법을 해소하기 위해 이진 탐색 트리를 이용할 수 있다.
이진 탐색 트리를 이용한 구현 방법
이진 탐색 트리
이진 트리에서 한가지 규칙을 추가한 자료구조이다. 이진 트리에서 왼쪽 서브 트리는 루트보다 작은 값이 모여있고 오른쪽 서브 트리는 루트보다 큰 값이 모여있도록 구성되어 있는 트리이다.
이진 탐색 트리 요소 추가
- 먼저 5를 추가하면 root 가 5가 된다.
- 다음으로 4를 추가한다. 4는 root 인 5보다 작기 때문에 왼쪽 정점에 위치한다.
- 다음으로 7을 추가한다. 7은 root 인 5보다 크기 때문에 오른쪽 정점에 위치한다.
- 다음으로 8을 추가한다. 8은 root 인 5보다 크기 때문에 오른쪽 정점으로 이동하고 서브트리인 root 인 7 보다 크기 때문에 7의 오른쪽 정점에 위치한다.
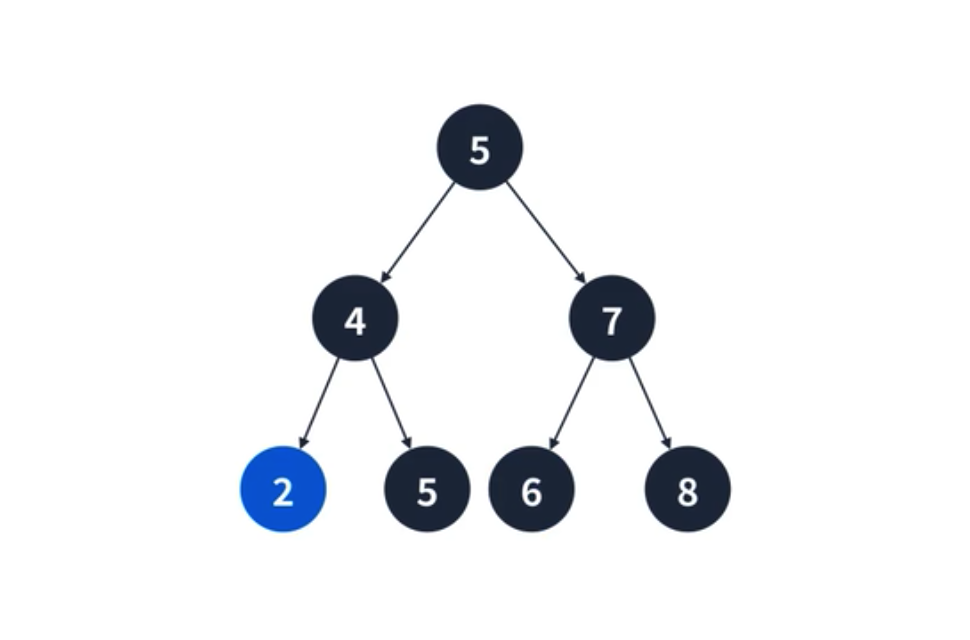
- 이번엔 root 와 동일한 값인 5를 추가한다. 동일한 경우 왼쪽 또는 오른쪽 아무곳에 넣어도 상관 없지만 여기선 왼쪽 정점에 넣어보자. 4보다는 크기 때문에 4의 오른쪽 정점에 추가된다.
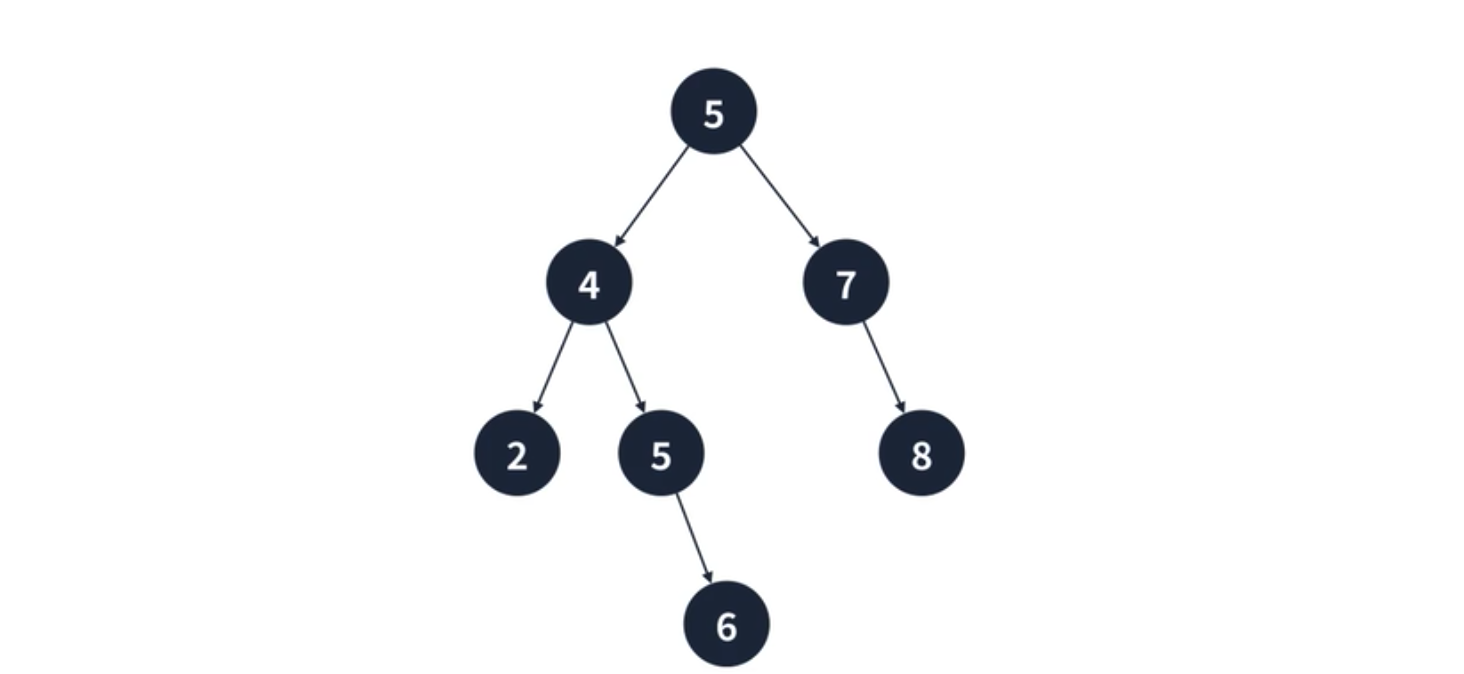
- 이번엔 6을 추가해보자. 6은 5보다 크고 7 보다 작기 때문에 7의 왼쪽 노드에 추가된다.
- 마지막으로 2를 추가해보자. 2는 5보다 작고 4보다 작기 때문에 4의 왼쪽 정점에 추가된다.
이진 탐색 트리 요소 삭제
단말 정점, 즉 leaf 노드를 삭제하는 경우에는 단순하다. 별다른 처리 없이 부모 정점과의 연결을 끊으면 자연스럽게 제거된다.
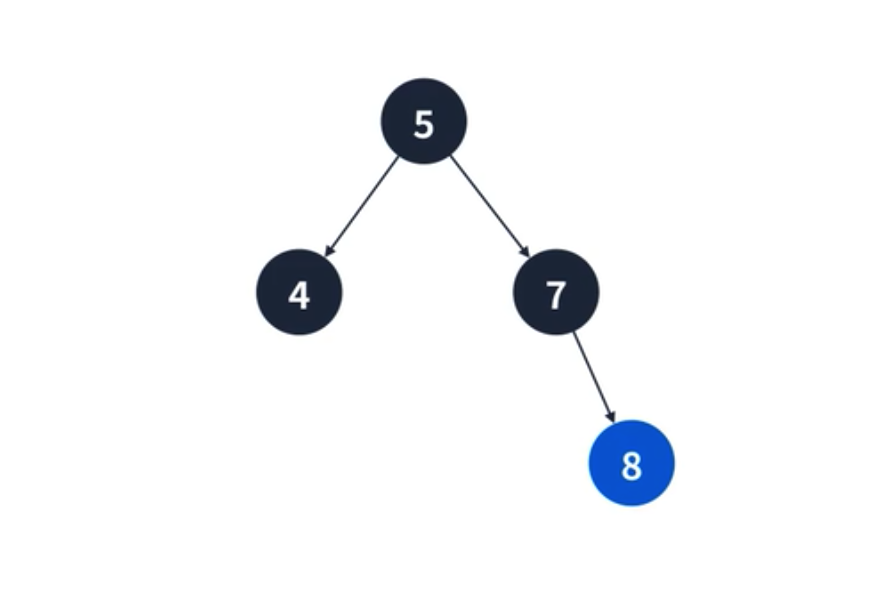
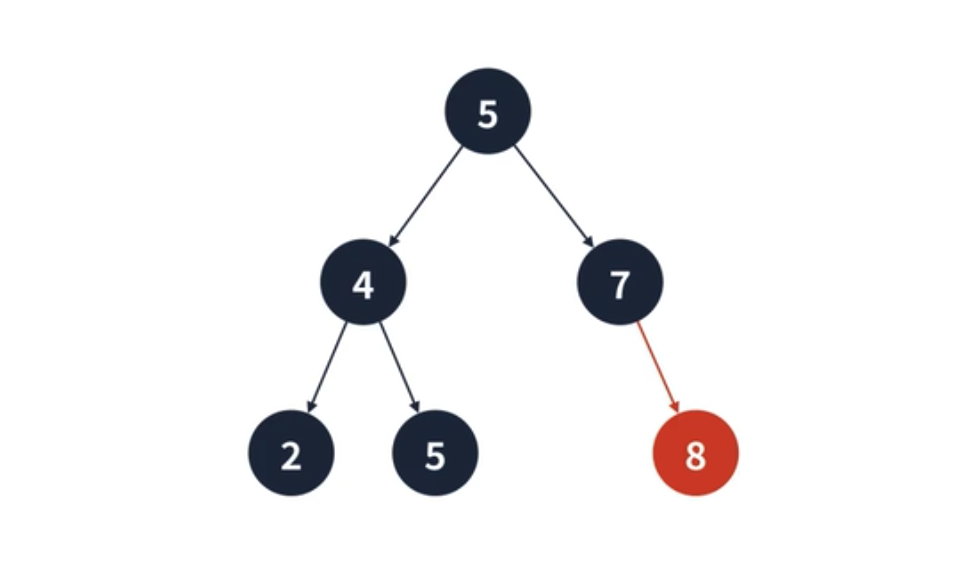
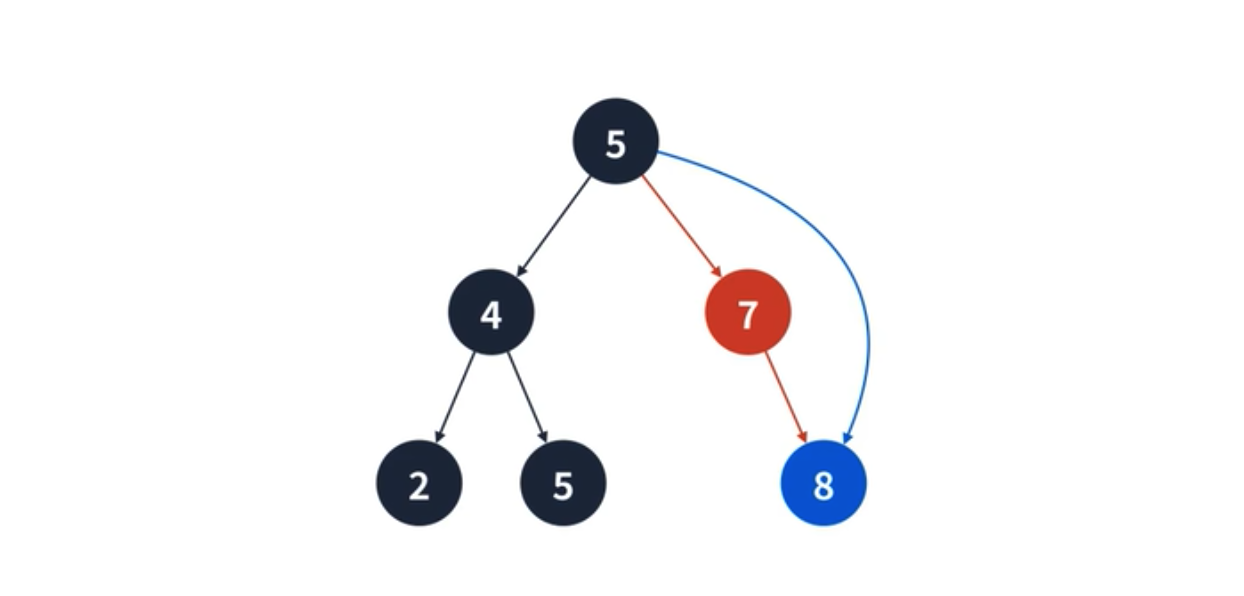
하나의 서브 트리를 가지는 경우, 제거되는 정점의 부모 간선을 자식 정점을 가르키게 바꾸면 된다. 예를 들어 아래의 그림처럼 7을 제거할 경우에 5의 오른쪽 간선을 8을 가리키도록 수정하면 된다.
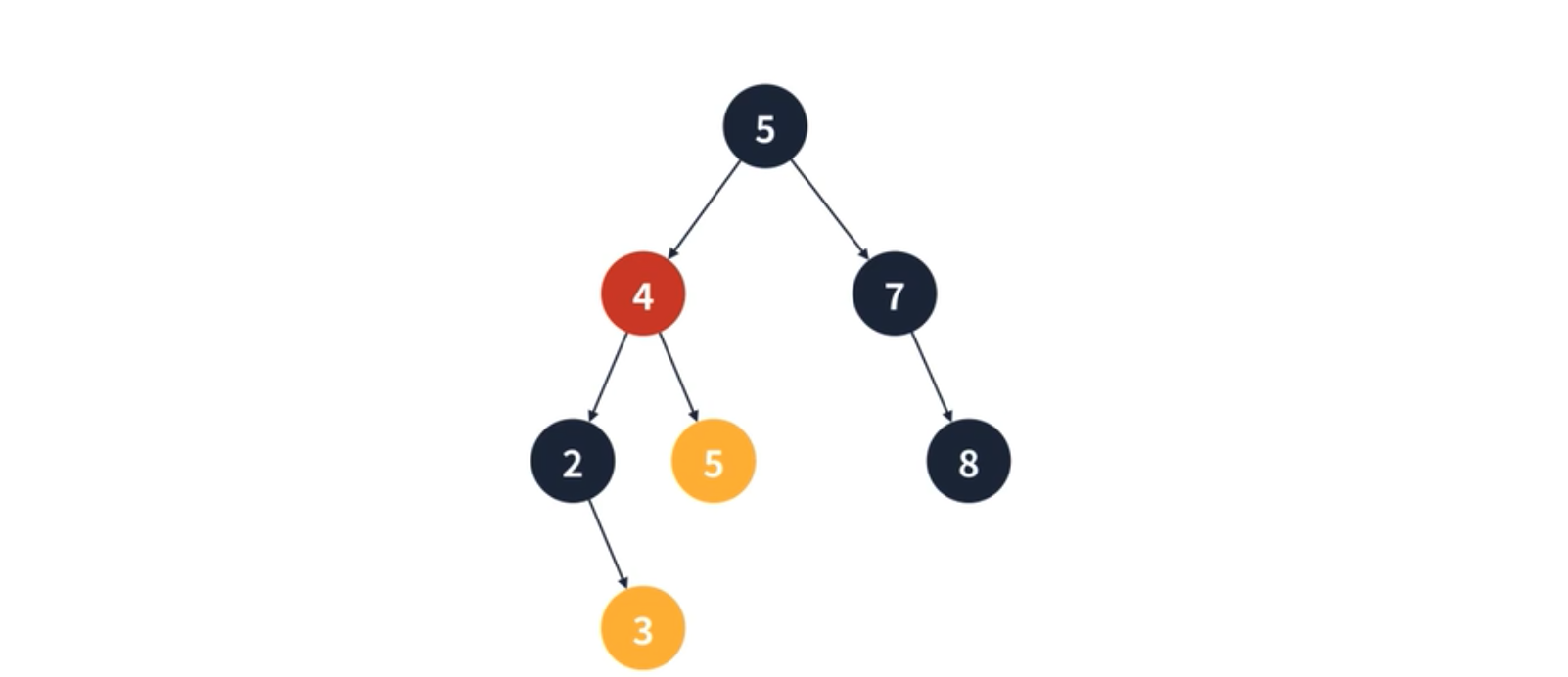
두 개의 서브 트리를 가지는 경우, 조금 복잡하다. 둘중 하나를 선택하면 되는데 왼쪽 서브 트리의 가장 큰 값 혹은 오른쪽 서브 트리의 가장 작은 값과 교체하면 된다. 예시를 보면 4를 삭제할 때 3 혹은 5 에 해당하는 정점과 교체하면 된다. (교체된 정점의 좌우 자식이 없다면 제거되는 정점의 링크로 대체된다.)
이진 탐색 트리의 문제점
굉장히 자주 발생할 수 있는 문제점이다.
- 먼저 5를 추가한다. root 정점이 된다.
- 4를 추가한다. root 정점의 왼쪽 정점이 된다.
- 3을 추가한다. 또 왼쪽 정점으로 삽입된다.
- 2를 추가한다. 또 왼쪽 정점으로 삽입된다.
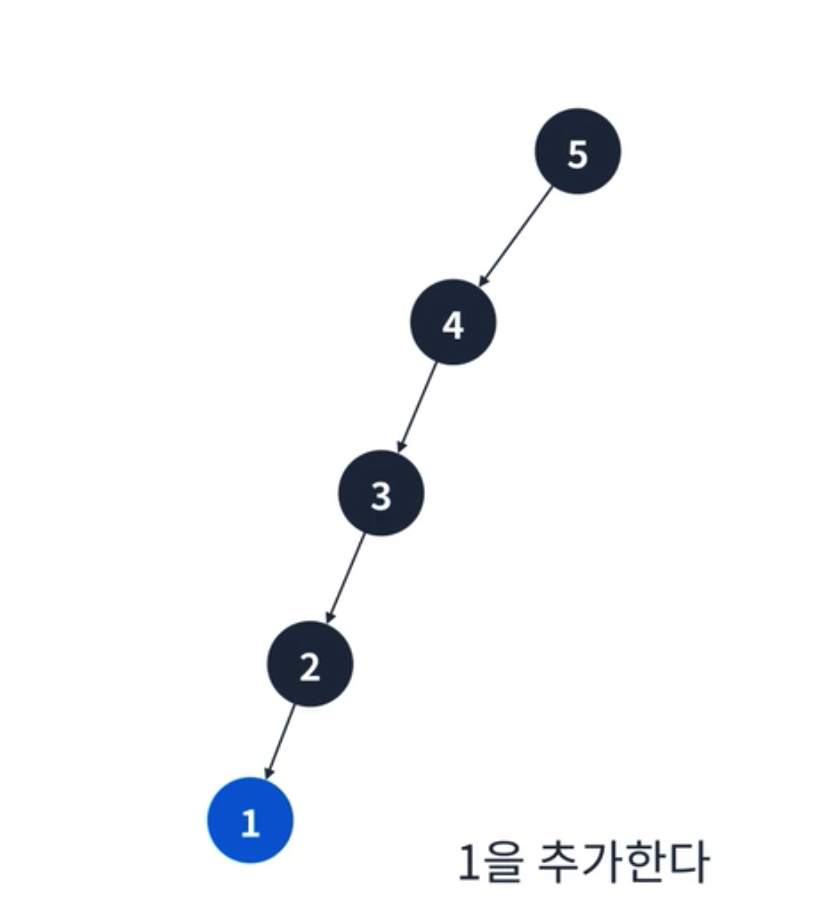
- 1을 추가한다. 또 왼쪽 정점으로 삽입된다.
위의 예시처럼 이진 탐색 트리는 최악의 경우 한쪽으로 편향된 트리가 될 수 있다. 그래서 이런 경우에는 순차 탐색과 동일한 시간복잡도를 가진다. 이를 해결하기 위해 AVL 트리, 레드-블랙 트리 자료구조를 이용할 수 있다. AVL 트리, 레드-블랙 트리 자료구조를 이용하면 이진 탐색 트리의 균형을 맞춰줄 수 있다.