🔍 Problem

1003 피보나치 함수

---

⚡️ 사용한 알고리즘

---

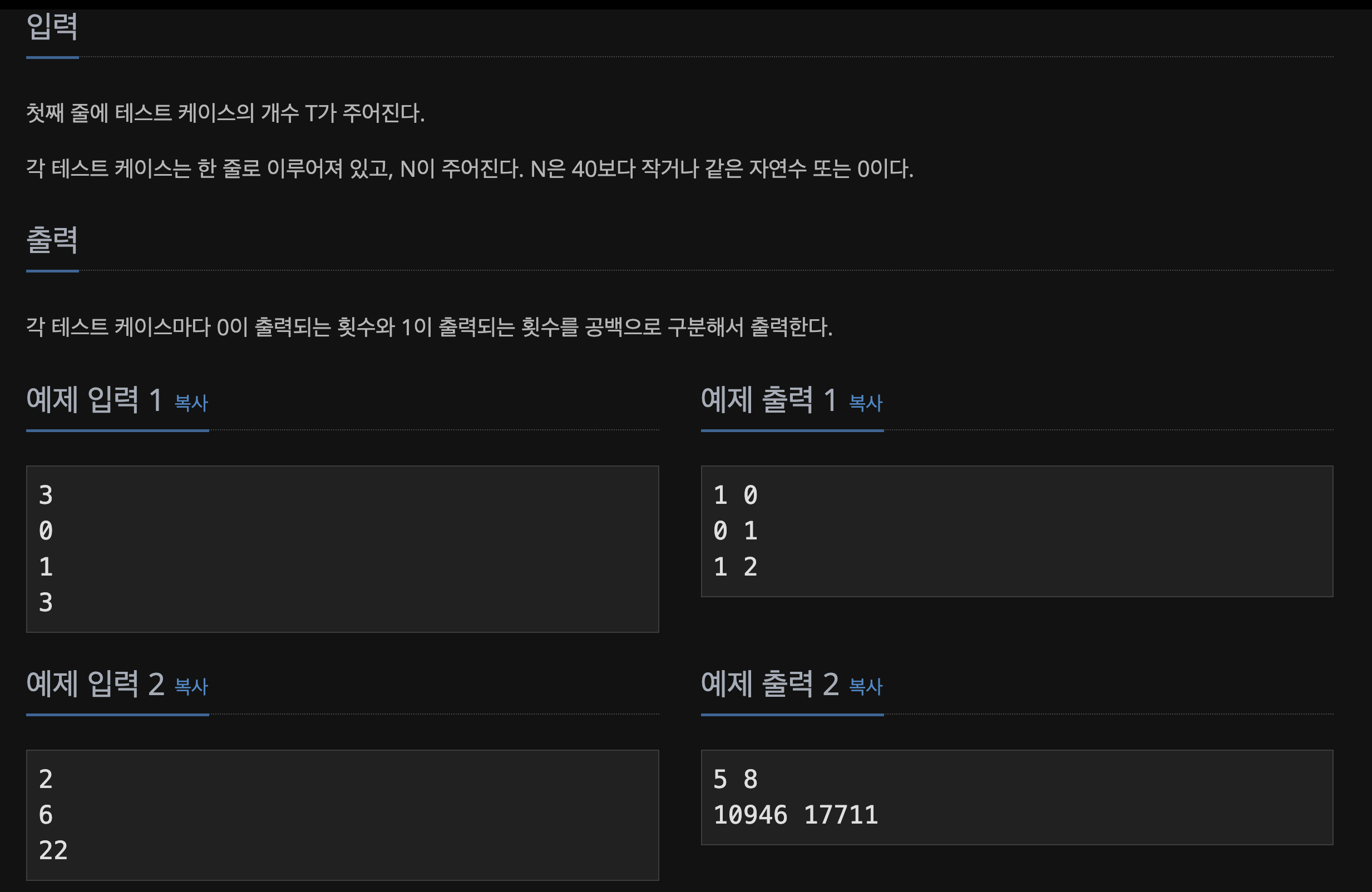
📃 Input&Output

---

📒 해결 과정

1️⃣ 피보나치 함수 트리를 그려보면 이진트리가 다음과 같이 나온다.

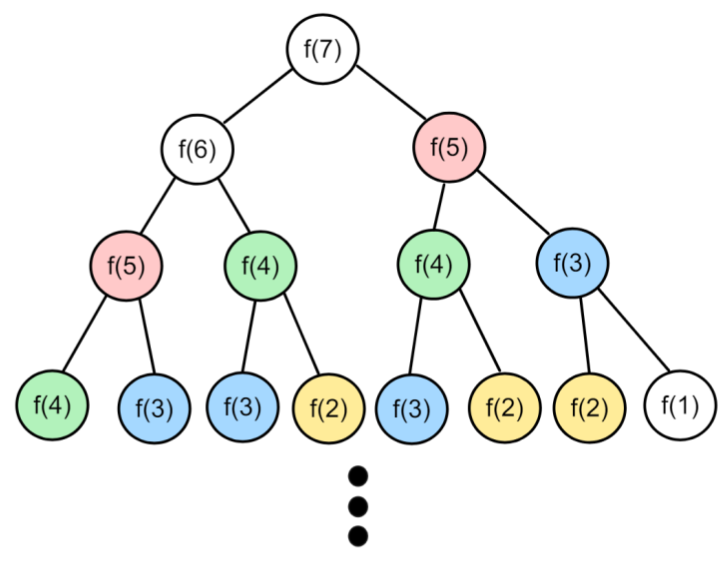
사진에서 f(7)의 f(3)의 개수를 구하려면 f(6)의 f(3)의 개수와 f(5)의 f(3)의 개수를 더하면 된다. 이것을 점화식으로 나타내보면

$f_k(n) = f_k(n-1) + f_k(n-2)$
$f_k = f(k) \quad트리에서\quad가지고\quad 있는\quad f(n)의 개수$

2️⃣ 따라서 1과 0의 dp 배열을 각각 선언해주고 40까지 위의 공식을 사용하여 채운 다음, 원하는 인덱스를 넣어서 프린트해주면 된다.

---

❗주의점

1. 여백

---

💻 Code

simport sys

T = int(sys.stdin.readline())

dp0=[0]*41
dp1=[0]*41

dp0[0]=1
dp1[0]=0

dp0[1]=0
dp1[1]=1

dp0[2]=1
dp1[2]=1

for i in range(3,41):
    dp0[i] = dp0[i-1] + dp0[i-2]
    dp1[i] = dp1[i-1] + dp1[i-2]
    



for _ in range(T):
    n=int(sys.stdin.readline())
    print(f"{dp0[n]} {dp1[n]}")

---

🤔 느낀점

난이도는 높지 않았지만 점점 DP에 대한 감을 찾게해주는 문제다. 가장 중요한건 점화식을 어떻게 할 것인가도 이지만, 이전 값이 다음 값에 영향을 줄 때 어떠한 방식으로 영향을 주는가를 생각하는 것이 시간 단축의 핵심일 것 같다.

위 같은 경우의 어떠한 방식은 "f(n-1)과 f(n-2)의 트리가 합쳐져서 f(n)의 트리를 만든다"는 것이다.

결국은 문제를 많이 풀어봐야한다. 그리고 트리 자료구조가 굉장히 중요한 것 같다.