[알고리즘] 백준 9095 1,2,3 더하기

Halo·2025년 4월 26일

DP 문제풀이 알고리즘

Algorithm

목록 보기

26/85

🔍 Problem

9095 1,2,3 더하기

⚡️ 사용한 알고리즘

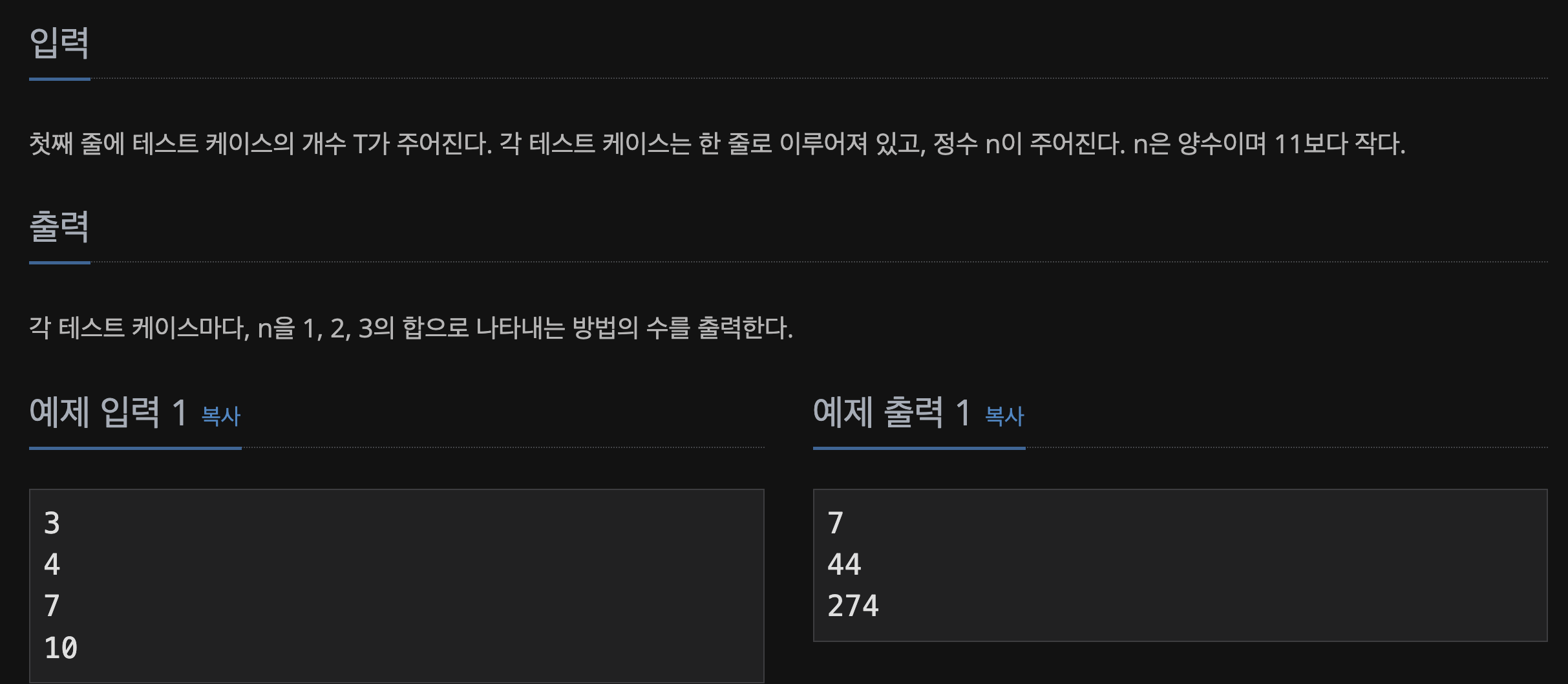
📃 Input&Output

📒 해결 과정

1️⃣ 1부터 1,2 그리고 3의 덧셈 조합으로 되는 경우의 수를 구해본다.

No	경우의 수	Count
1	(1)	1
2	(1+1,2)	2
3	(1+1+1), (1+2), (2+1), (3)	4
4	(1+1+1+1), (1+1+1+2)x4 (2+2)x1, (1+3)x2	7

2️⃣ 자세히보면 4는 다음과 같다.
가. 4 = 3 + 1

4는 3을 구성하는 경우의 수에서 1을 더하면 4가 만들어진다.
ex. 3은 (1+1+1)을 가지고 있고
	4=(1+1+1+1)이다. 그렇다 3의 경우의 수 중 하나에서 1을 더한 것이 4의 경우의 수에도 포함 되는 것이다.

나. 4 = 2 + 2

위의 (가) 원리에 따르면 2를 구성하는 경우의 수 뒤에 2를 더해주면 4의 경우의 수 중 일부가 된다.

4=1+3을 생각하면 1의 경우의 수들에서 3을 더한 것이 4의 경우의 수들 중의 일부가 된다는 말이다.
(n+1, n+2, n+3까진 하였고 n+4는 생각할 필요가 없다. 왜냐하면 이 문제는 1, 2 그리고 3의 조합으로 이루어져야 하기 때문이다.)

3️⃣ 따라서 다음 식으로 나태낼 수 있다.
$dp[i] = dp[i-1] + dp[i-2] +dp[i-3]$ 인것이다.

점화식을 찾았으니 1,2,3까지는 dp에 할당해놓고 4~11까지 구하면 될 것이다.

메모리 및 시간 고려

메모리가 512이고 n은 정수인 11이하인 수 이므로 메모리는 충분하다. 연산은 1초로 11까지 순차탐색하는 경우의 수이므로 아무리 T가 커봤자 2000만번 이하이므로 충분하다.

❗주의점

DP를 사전에 구해놓고 원하는 Index를 탐색하는 방법으로 해결해야 시간을 줄일 수 있다. 매번 DP 리스트를 생성할 필요가 없단 뜻이다. 왜냐하면 n이 11이하라서 배열 크기가 아무리 커봤자 12 이하기 때문이다.

💻 Code

import sys
import math
N=int(sys.sㄹtdin.readline())
dp=[0]*(N+1)

dp[1]=0

# dp[i] = 1 + min(dp[i//2], dp[i//3], dp[i-1])
for i in range(2,N+1):
    
    # v1 : dp/3, v2 : dp/2, v3 : dp[i-1]
    v1,v2,v3=math.inf,math.inf,dp[i-1]    
    
    if i%3==0:
        v1=dp[i//3]
    if i%2==0:
        v2=dp[i//2]
    
    dp[i]=1+min(v1,v2,v3)

print(dp[N])