🔍 Problem

11726 2×n 타일링

---

⚡️ 사용한 알고리즘

DP

---

📃 Input&Output

---

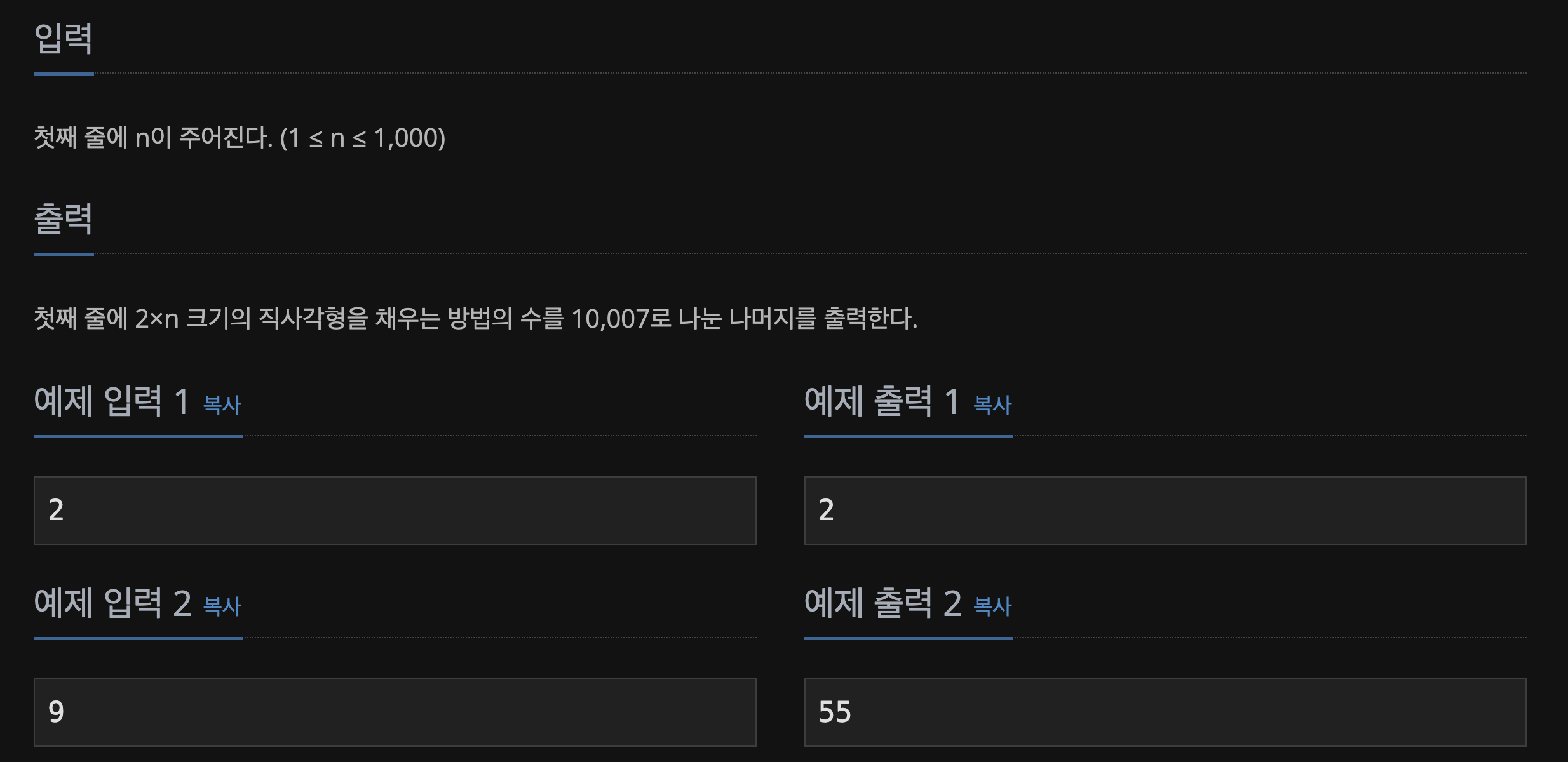
📒 해결 과정

1️⃣ 각 경우의 수를 차례로 구해본다.

n	2xn 크기의 직사각형을 채우는 방법의 수
1	1
2	2
3	3
4	5
5	8

2️⃣ 다음과 같이 점화식을 구할 수 있다.
$dp[i]=dp[i-1]+dp[i-2]$

---

❗주의점

가. 꼭 문제의 흐름을 파악할 필요가 없다.😂
필자는 위 문제를 풀때, n=3인 경우, n=2인 경우에 양쪽에 +1을 하는 경우의 수를 생각하고 중복을 제거하려고 노력했지만 결국 성공하지 못했다. 그래서 답지를 봤는데 단순히 숫자의 규칙로만 점화식을 구성하는게 아닌가? 정말 통탄스럽고 벽을 깬 느낌이였다. 따라서 필자는 앞으로 다음과 같이 DP문제를 접근할 것이다.

1. 단순히 "숫자의 규칙"만 보고 점화식을 세워보자
2. 그래도 안되면 그림을 그려보며 구하려는 점화식의 직관적인 "패턴(원리)"을 찾아보자.

나. DP배열 범위 선언 문제

dp =[0] *1001

# 주의점 나. : 인덱스 에러 (n=1 일때, dp[2]가 존재하지 않음.)
# dp =[0] *(n+1)

dp[1] = 1
dp[2] = 2

---

💻 Code

import sys
input = sys.stdin.readline

n = int(input())


dp =[0] *1001

# 주의점 1 : 인덱스 에러 (n=1 일때, dp[2]가 존재하지 않음.)
# dp =[0] *(n+1)

dp[1] = 1
dp[2] = 2

for i in range(3,n+1): 
    dp[i] = (dp[i-1] + dp[i-2])
print(dp[n] % 10007)

---

🤔 느낀점

굉장히 단순한 문제지만 정말 많은 것을 배웠다. 역시 머리를 싸맨만큼 돌아오는 것 같다. 오늘도 하나의 벽을 깬 느낌이였다. 그리고 논술 풀때 쓴 ∵ ∴ (왜냐하면. 그러므로) 기호들을 사용하니까 노트에 문제 풀 때 굉장히 수월했다. 많이 써야겠다는 생각이 들었다. 꼭 기억하자, DP문제를 풀 때, 첫번째는 단순한 수열의 규칙을 찾아보기, 그래도 안되면 문제의 패턴을 찾아보기!

---

📝 출처

1. jie0025님의 Tistory