[알고리즘] 백준 12865 평범한 배낭

Halo·2025년 4월 30일

DP 문제풀이 알고리즘

Algorithm

목록 보기

30/85

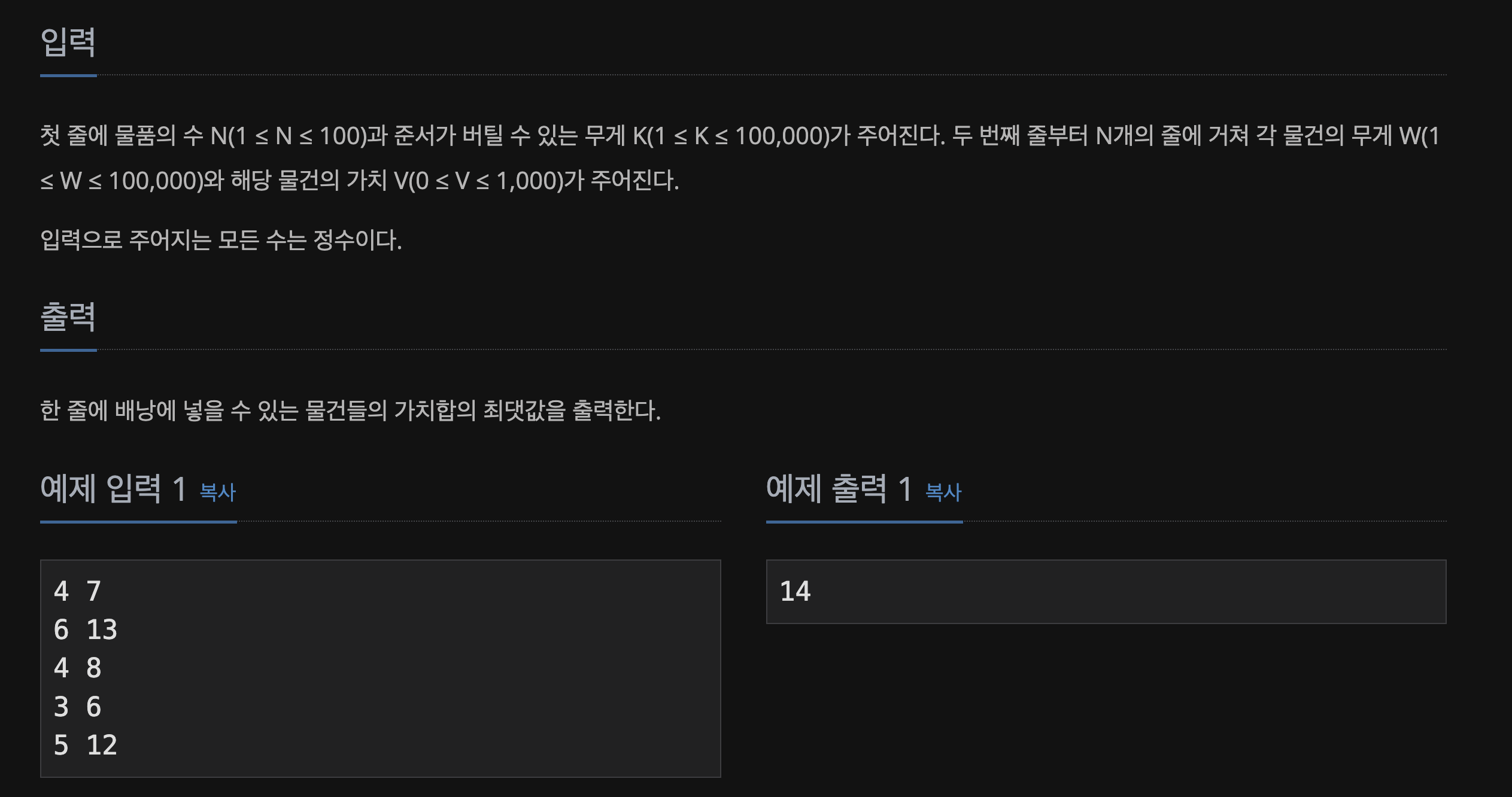
🔍 Problem

12865 평범한 배낭

📃 Input&Output

📒 해결 과정

1️⃣ DP 매트릭스를 그린다.

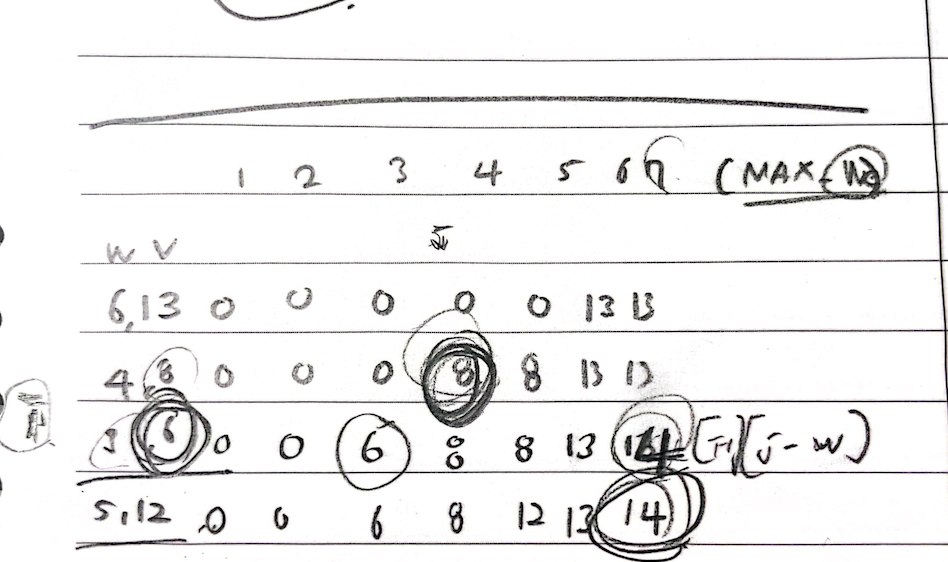
세로 : 가방에 넣을 수 있는 최대 무게
가로 : 각 물건의 무게(w)와 가치(v)
좌표 값 : 최대 가치

가. 생각해야할 것

1. 배낭에 물건을 넣기 전과 후로 나눈다.
배낭에 물건을 넣을 수 있다는 것은 현재 넣는 무게가 최대무게보다 작은 경우고, 현재 물건을 넣기 전의 (최대무게 - 현재무게)가 최대무게인 좌표값을 찾아가면된다. 예를들어 (3,6)행에의 최대무게(가로)가 7인 경우를 생각해보자

현재 최대 무게 : 7

무게 3, 가치 6 짜리 물건 넣고난 후 무게 : 4 (7-3)
따라서 4짜리 무게를 가진 물건을 더 넣을 수 있고 그것은 이전 행의 최대 무게가 8인 값이다. 그리고 이것이 이전 행의 값보다 크다면 이것을 채택하는 것이다.

2. 왜 이전 행인가?
위 매트릭스의 의미는 현재 좌표값은 현재 행을 포함한 이전의 물건들을 넣고 최대 무게를 지정한 경우의 최대값이다. 따라서 DP특성상 이전 제한한 무게의 최선값을 계속해서 저장해 나가고 있는 memorization 기법을 쓰고 있는 것고 이전 행은 이 물건을 넣기 전의 무게별 최대가치에 대한 정보를 가지고 있는 리스트가 되는 것이다.

2️⃣ 결론 및 점화식

가. 만약 현재 넣으려고 하는 무게가 최대 무게 보다 작다면?

현재 무게의 가치와 "그것을 뺀 넣을 수 있는 무게(최대무게-현재무게)"의 최대 가치를 합쳐주면 된다.

$dp[i][j]=dp[i-1][j]$

나.현재 넣으려고 하는 무게가 최대 무게 보다 크다면?

이전행의 같은 최대무게 값을 가져오면 된다.

$dp[i][[j]=max(dp[i-1][j],dp[i-1][j-w(현재무게)]+v(현재 물건의가치)$

💻 Code

import sys

N, K = map(int, sys.stdin.readline().split())

item = [list(map(int, sys.stdin.readline().split())) for _ in range(N)]

dp = [[0] * (K + 1) for _ in range(N + 1)]


# N (1~N)
# K (1~K)

for i in range(1, N + 1):
    w, v = item[i - 1]
    for j in range(1, K + 1):
        if w > j:
            dp[i][j] = dp[i - 1][j]
        else:
            dp[i][j] = max(dp[i - 1][j], dp[i-1][j-w]+v )
            
print(dp[N][K])