🔍 Problem

2579 계단오르기

---

⚡️ 사용한 알고리즘

DP

---

📃 Input&Output

---

📒 해결 과정

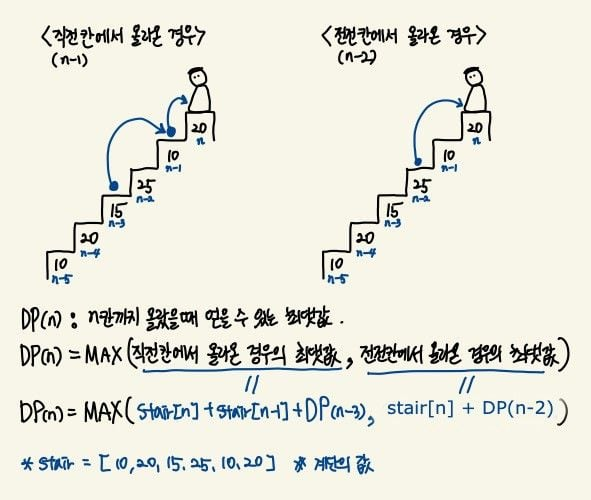
1️⃣ n번째 계단에 왔을 때, 전에 어떤 계단을 거쳐왔는지를 생각해본다.
2️⃣ 3개의 계단을 연속으로 올 수 없기에, 거칠 수 있는 계단은 n-1과 n-2밖이 없다.
	➊ n-1 계단 : n-3 -> n-1 -> n 순으로 계단을 거친 것이다.(이 과정의 식에서 3개 계단이 연속으로 올 수 없는 제약 조건을 걸 수 있다.)
    ➋ n-2 계단 : n-2 -> n 순으로 계단을 거친 것이다.
3️⃣ 위의 2개 Case 중 더 큰 값이 n번째 계단까지 올라온 최대값이 된다.

---

❗주의점

1. dp식에 문제의 규칙 넣기 ( 이 문제의 규칙 : 이어진 3개의 계단을 오를 수 없다.)

---

💻 Code

import sys

N = int(sys.stdin.readline())

stair = [0] * (301)
dp = [0] * (301)

for i in range(1, N + 1):
    stair[i] = int(sys.stdin.readline())

dp[1] = stair[1]
dp[2] = stair[2] + stair[1]
dp[3] = max(stair[1] + stair[3], stair[2]+stair[3])

for i in range(4, N+1):
    dp[i] = max(dp[i-2]+stair[i], dp[i-3]+stair[i-1]+stair[i])
    
print(dp[N])

---

🤔 느낀점

1. DP를 풀 때는 결과론적인 생각을 하자
즉, 뒤에거는 앞에것들을 가지고 완성시키는 것이다. 이 문제의 핵심은 일단 뒤에있는 계단을 올라갔다는 전제하에, 어떤 방식으로 올라올 수 있는지에 대한 경우의 수를 생각하고 그 경우의 수들 중에 최대값을 구하는 문제였다.

---

📝 출처

v3.leedo.m