Few-shot Learning for Multi-label Intent Detection

LEE HANBIN·2022년 11월 28일
논문읽기
0

논문

목록 보기
6/8

Abstract

논문에서는 사용자의 발화 의도(intent detection)를 예측하기 위하여 few-shot multi-label classification을 연구하였습니다. 기존 SOTA 모델은 label과 instance 사이의 연관성을 예측하고, threshold 값을 설정하여 instance와 연관된 모든 label을 선택했습니다. 논문은 데이터가 적은 환경에서 적절한 threshold를 설정하기 위해, 데이터가 풍부한 도메인에서 보편적인 threshold 값을 학습하였습니다. 다음으로 non-parameteric learning을 기반으로 threshold 값을 특정한 few-shot 도메인에 적용하였습니다. 또한, label-instance relevance score을 더 잘 계산하기 위하여 representation space에서 anchor point로 label name을 embedding 하였습니다. 이로 인해, 다른 class를 갖는 representation은 더 잘 나뉠 수 있었습니다. 2개의 데이터셋으로 진행한 실험을 통해, 논문에서 제안한 모델이 one-shot, five-shot 환경에서 baseline 모델을 능가하는 성능을 보이는 것을 확인했습니다.

Problem

Task-oriented Dialogue system에서 intent detection은 기본 구성 요소입니다. 하나의 발화에 동시에 여러 개의 의도가 담겨있을 수 있기 때문에 Multi-Label Classification (MLC)이 주목받고 있습니다. 실제 환경에서는 대화 도메인과 task가 급격하게 변하고, 새로운 domain이 나타나면 intent detection을 위한 학습 데이터가 부족할 수 있습니다.

Few-Shot Learning (FSL)은 위와 같은 학습 데이터가 부족한 문제에 대한 해결책이 될 수 있습니다. FSL은 사람과 같이 데이터를 구분하는 방법을 학습하고, 이 학습 경험을 few-shot example에 적용합니다. 그러나 multi-label 문제에서는 하나의 샘플이 여러 개의 label을 가질 수 있기 때문에 FSL에서 사용하는 유사도 기반 방법론이 효과적이지 못합니다. 또한, label을 위한 적절한 threshold 값을 결정하는 것이 어렵습니다.

Method

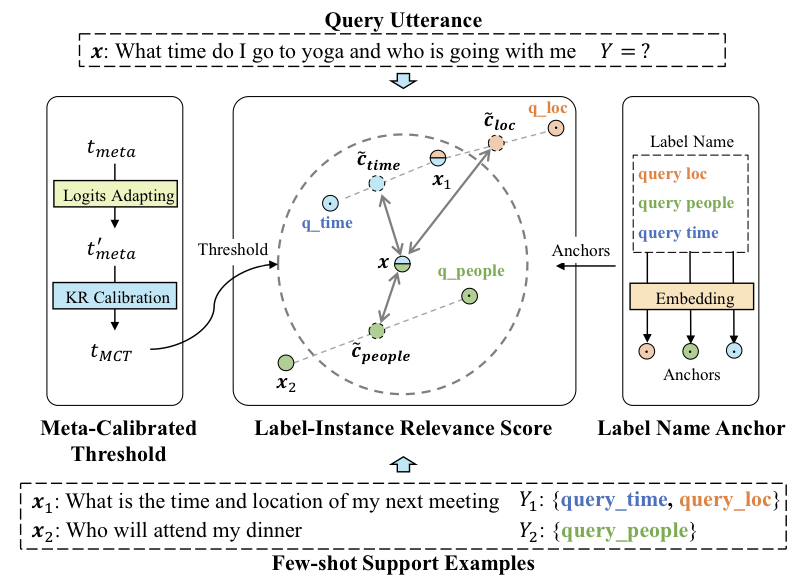
논문에서 제안한 framework의 전반적은 흐름은 위와 같습니다. 각 query xx에 대하여 label-instance relevance score를 계산합니다. 이 때, 그 값은 Anchored Label Representation c~\tilde{c} 와의 유사도를 표현한 값입니다. 다음으로 Meta-Calibrated Threshold mechanism을 통해 얻은 threshold 값 tt보다 score가 큰 label을 모두 선택합니다.

1. Proposed Framework for Few-shot Multi-label Intent Detection

이 논문에서 제안한 framework는 다음과 같이 표현 가능합니다.

Y=h(x,S)={y∣f(x,y,S)>t,y∈Y}Y=h(x,S)=\{y|f(x,y,S)>t,y \in \mathcal{Y}\}

여기서 ff는 label-instance relevance score를 연산하는 함수이고, tt는 threshold 값 입니다.

Few-shot multil-label classification을 위한 함수 ff는 일반적인 유사도를 기반으로 점수를 계산합니다. 먼저, support set SS로부터 각 label에 대한 representation을 얻습니다. cic_i 를 label yiy_i 의 representation vector이라고 할 때, query sentence xx와 label yiy_i 간의 relevance score는 아래와 같습니다.

f(x,yi,S)=SIM(E(x),ci)f(x,y_i,S)=SIM(E(x),c_i)

위 식에서 E(⋅)E(\cdot) 은 embedding 함수를 의미합니다. BERT 모델을 embedder로 사용했고, sentence embedding E(x)E(x)는 BERT output token들의 평균입니다.SIMSIM은 유사도 함수로, dot-product similarity (내적) 을 사용했습니다. Label Representation이 잘 나뉘도록 하기 위해, 논문에서는 Anchored Label Representation으로 cic_i를 계산했습니다. 다음으로, threshold 값 tt를 적절하게 설정하기 위하여 source domain으로 부터 얻은 사전 지식과 target domin에서 관찰한 값을 통합하였습니다. 이를 위해, 논문은 Meta Calibrated Threshold를 제안했습니다.

2. Meta Calibrated Threshold

Few-shot learning에서는 모델을 학습할 때와 테스트 할 때 데이터의 domain이 다르기 때문에 threshold 값이 다를 수 있습니다. 또한, instance에 따라서 label 수와 label-instance relevance score의 밀도가 다를 수 있기 때문에, 각 instance가 서로 다른 threshold 값을 갖고 label을 하도록 해야 합니다.

2.1. Meta Threshold with Logits-Adaptiveness

Domain의 특성을 고려한 threshold 값을 찾기 위해서, 논문에서는 Meta Threshold를 제안합니다. Meta Threshold tmetat_{meta}는 각 domain에 특성을 고려(automatic adaptability)하면서, 다양한 domain에 최적화(jointly optimized on various domains)하여 threshold 값을 예측하는 방법입니다.

Instance 마다 relevance score의 scale과 density과 다릅니다. 그리고 threshold 값은 항상 relevance score의 최대값과 최소값 사이에 존재합니다. Query와 domain의 특성을 반영하는 threshold를 설정하기 위해 Logit-Adaptive mechanism은 score의 최대값과 최소값의 interpolation을 사용합니다. 이를 수식으로 표현하면 아래와 같습니다.

tmeta=T(x,S)=r max∀y∈Y f(x,y,S)+(1−r) min∀y∈Y f(x,y,S)t_{meta}=T(x,S)=r~\underset{\forall y \in \mathcal{Y}}{max}~f(x,y,S)+(1-r)~\underset{\forall y \in \mathcal{Y}}{min}~f(x,y,S)

T(⋅)T(\cdot)은 thresholding 함수를 의미하며, rr은 source domain으로부터 학습한 interpolation rate 입니다.

22

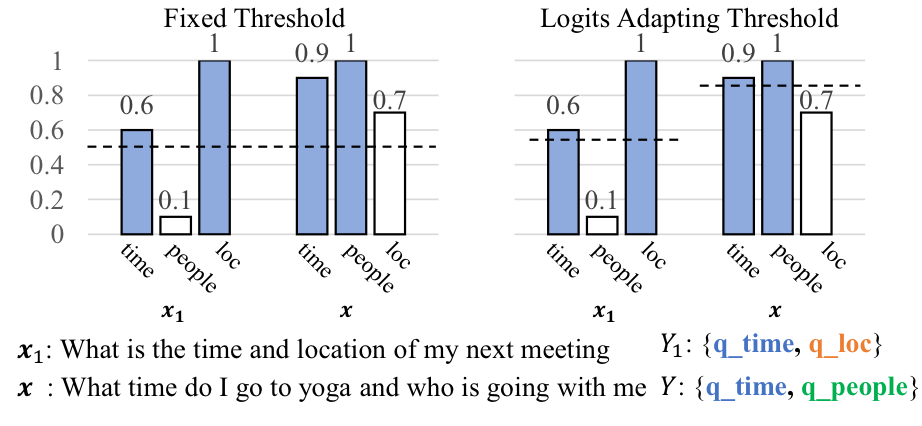
위 그림은 fixed threshold와 logit-adapting threshold의 예시입니다. 색칠된 score bar는 정답 label을 의미합니다. x1x_1과 xx의 정답 label을 모두 맞출 수 있는 fixed threshold는 존재하지 않습니다. 그러나, logit-adapting threshold는 r=0.5r=0.5일 때, 두 케이스에서 모두 정답을 맞출 수 있습니다.

위 예시에서 살펴보았듯이, Interpolation-based threshold를 사용하면 label-instance relevance score의 density에 따라 다르게 threshold 값을 설정하기 때문에, query 마다 threshold가 다르게 됩니니다.

2.2. Threshold Calibration with Kernel Regression

Meta Threshold tmetat_{meta}으로 다양한 domain에 일반화된 threshold를 구할 수 있지만, target domain에 특화된 정보는 부족하게 합니다. 이를 해결하기 위해, support set으로부터 domain/query-specific threshold testt_{est}를 예측하고, 이 값을 Meta threshold tmetat_{meta}를 조정하는데 사용합니다. 정답 threshold 값에 대한 정보는 주어지지 않기 때문에 모델이 threshold를 예측하도록 학습할 수는 없었습니다. 대신, label의 수를 예측하고, threshold 값을 간접적으로 추론하였습니다.

Domain 정보를 활용하여 label 수를 예측하기 위해서 Kernel Regression (KR)을 사용하였고, query의 label 수를 support set과의 유사도로 추정하였습니다. KR은 non-parametric method이므로, 보지못한 domain에 대해서도 tuning 없이 동작할 수 있습니다. KNN과 같은 다른 non-parametric regression method과 달리, KR은 모든 support set을 사용하고, distance influence(유사도 정도)를 고려합니다.

Support set SS가 주어졌을 때, query xx의 label 개수 nn은 support set의 label 개수의 weighted average으로 추정하였습니다. 여기서 weighted average는 query와 support set 간의 kernel similarity로 계산됩니다.

n=1Z∑∀(x′,y′)∈SKernel(E~(x),E~(x′);λ)⋅∣y′∣n=\cfrac{1}{Z}\underset{\forall(x',y')\in S}{\sum}Kernel(\tilde{E}(x), \tilde{E}(x');\lambda)\cdot|y'|

ZZ는 normalizing factor이고, Gaussian Kernel: Kernel(a,b;λ)=exp(−(a−b)2/λ)Kernel(a,b;\lambda)=exp(-(a-b)^2/\lambda) (단, λ\lambda는 bandwidth factor) 를 사용했습니다. E~(x)\tilde{E}(x)는 feature extractor로 sentence xx의 label 개수와 연관된 feature vector을 반환합니다. Indent detection task를 위해 논문에서는 문장에 담긴 의도 개수와 관련된 언어학적 특징(접속사 수, 술어 수, 구두점 수, 질문 대명사 수, ...)을 고려하고 MLP projection layer에 encoding 하였습니다. 그리고, domain/query-specific threshold testt_{est}를 예측한 label number nn으로부터 얻었습니다. 구체적으로, xx의 top-nn label-instance relation score threshold를 필터링하는 threshold value testt_{est}를 구하였습니다. 한 가지 직관적인 아이디어는 (n+1)th(n+1)_{th}번째로 큰 score을 threshold로 사용합니다. 그러나 이 값은 하나의 label-instance relevance score로부터 얻습니다. 따라서, 학습된 kernel weights로 threshold 값을 추정하여 모든 relevance score을 활용할 수 있도록 개선하였습니다.

test=1Z∑∀(x′,y′)∈SKernel(E~(x),E~(x′);λ)⋅T′(∣y′∣;x,S,f)t_{est}=\cfrac{1}{Z} \underset{\forall(x',y') \in S}{\sum} Kernel(\tilde{E}(x),\tilde{E}(x');\lambda)\cdot T'(|y'|;x,S,f)

T′(∣y′∣;x,S,f)T'(|y'|;x,S,f)는 query xx의 (n+1)th(n+1)_{th} 큰 label-instance relevance score를 반환하는 함수입니다. 마지막으로, query-specific threshold testt_{est}을 활용하여 domain-general meta threshold tmetat_{meta} 값을 조정합니다. Query xx의 최종 threshold 값은 아래와 같이 연산됩니다.

(1)

t=α×Tmeta+(1−α)×testt=\alpha \times T_{meta}+(1-\alpha) \times t_{est}

이 때, α\alpha는 tmetat_{meta}와 testt_{est} 중 어떤 값에 우선 순위를 둘지 결정하는 hyper-parameter 입니다.

3. Anchored Label Representation

Label-instance relevance score을 계산하기 위해서는 label representation이 필요합니다. Label-instance similarity model의 품질을 높이기 위해서, label representation은 서로 잘 나뉘어야하며, 카테고리 정보에 대한 의미를 표현할 수 있어야 합니다.

3.1. Label Representation for Few-shot Learning

Few-shot Learning에서는 label representation을 주로 support set으로부터 얻습니다. Label yy의 프로토타입 representation은 support set의 averaged embedding 입니다.

ci=1Mi∑jMiE(xj)c_i=\cfrac{1}{M_i}\sum^{M_i}_j E(x_j)

각 xj∈{x∣(x,Y)∈S∧yi∈Y}x_j \in \{x|(x,Y) \in S \wedge y_i \in Y \} 는 yiy_i와 포함하는 support instance label을 의미하고, MiM_i는 support set 에서 해당 instance의 총 개수입니다. 그러나 이와 같은 방법은 multi-label 환경에서 다른 label이 같은 support set example을 공유할 수 있기 때문에 label representation의 모호함이 생길 수 있습니다.

3.2. Represent Label with Anchor

3.1에서 제시된 모호함을 제거하기 위해 카테고리가 다른 것을 강조하는 label-specific anchor를 제안합니다. Label-specific anchor는 label name의 semantic embedding 값을 anchor로 사용하고, 각 label을 support set example과 anchor로 표현하는 방법입니다. Anchor label representation ci~\tilde{c_i}는 다음과 같은 수식으로 표현합니다.

(2)

ci~=β×E(yi)+(1−β)×ci\tilde{c_i}=\beta \times E(y_i) + (1-\beta) \times c_i

cic_i는 3.1에서 설명했던 support set example을 활용한 프로토타입 representation이고, β\beta는 interpolation factor 입니다. label name의 embedding인 E(yi)E(y_i)는 프로토타입 representation vector이 서로 구분되도록 합니다. 이로 인해 label representation은 카테고리의 의미를 잘 표현할 수 있게 되어, 서로 잘 구분되게 됩니다.

4. Optimization

논문은 MLC framework를 few-shot learning episode(Vinyals et al. (2016))에 따라서 학습시켰습니다. 각 episode는 few-shot support set과 query set으로 구성되어있습니다. 데이터가 풍부한 domain에 대하여 few-shot simulation을 통해 학습하면 train과 test 단계에서 일관된 성능을 보장합니다. 또한, 프레임워크는 서로 다른 도메인에 최적화 되어, meta threshold tmetat_{meta}와 label-instance relevance scoring function ff가 domain을 일반화할 수 있습니다. 학습 시에는 Sigmoid Cross Entropy Loss를 사용하였습니다.

Loss=1N∑iN{I(yi∉Y∗)⋅σ(fyi)−I(yi∈Y∗)⋅σ(fyi)}Loss = \cfrac{1}{N} \sum^N_i \biggl\{ \mathbb{I}(y_i \notin Y^*) \cdot \sigma(f_{y_i}) - \mathbb{I}(y_i \in Y^*) \cdot \sigma(f_{y_i}) \biggl\}

N은 가능한 label의 개수이고, fyif_{y_i}는 f(x,yi,S)f(x,y_i,S)를 의미합니다. Y∗Y^{*}은 정답 label이고, I(⋅)\mathbb{I}(\cdot)은 indicator function으로 I(True)=1\mathbb{I}(True)=1이고, I(False)=0\mathbb{I}(False)=0 입니다. σ\sigma는 sigmoid function 입니다. Label 개수에 따라서 threshold를 선택하는 것은 공통 과정이므로 framework를 학습하기 전, kernel parameter를 pretrain 하였습니다.

Experiment

Source domain에서 학습한 지식을 학습할 때 보지못한 target domain에서 활용하여 1-shot/5-shot 환경에서 evaluation을 진행하였습니다.

1. Dataset

실험에는 여러 domain을 다루는 multi-indent dataset인 StandfordLU와 공공 dataset인 TourSG를 사용하였습니다. TourSG는 Itinerary (It), Accommodation (AC), Attraction (At), Food (Fo), Transportation (Tr), Shopping (Sh)에 관한 데이터 annotation이 존재하며, StandfordLU은 Schedule (Sc), Navigate (Na), Weather (We)가 annotation으로 존재합니다.

2. Few-shot Data Construction

Few-shot simulation을 위하여, data을 few-shot learning을 위한 형태로 재구성하였습니다. 각 sample은 query의 조합 (xq,yq)(x^q, y^q)과 일치하는 K-shot support set S\mathcal{S}로 이루어져있습니다. K-shot 환경에서는 instance에 여러 개의 label이 존재하기 때문에 label이 K time 나타날 것을 보장할 수 없습니다. 대신, Minimum-including Algorithm을 사용하여 support set이 다음 규칙을 만족하도록 합니다.

(1) 도메인에 존재하는 모든 레이블은 S\mathcal{S}에서 최소 K번 이상 나타남
(2) (x, y) 쌍을 label에서 제거된 경우, S\mathcal{S}에서 적어도 하나의 label이 K회 미만 나타남

각 domain에 대하여 NSN_S개의 서로 다른 K-shot support set을 만들고, 각 set에 대하여 NqN_q개의 query set을 포함하도록 하였습니다. 각 support-query-set은 하나의 few-shot episode를 의미합니다. 최종적으로 NSN_S개의 episode와, 각 도메인에 대한 Ns×NqN_s \times N_q 사이즈의 sample을 얻게 됩니다.

3. Evaluation

논문에서는 Few-shot 환경에서 robust 하게 evaluation을 진행하기 위하여, 서로 다른 도메인에서 5개의 random seed에 대하여 cross-validation을 진행하였습니다. 평가지표는 micro F1 Score을 사용하였습니다. Validation과 test는 각 각 1개의 domain에서 진행하였으며, 나머지는 학습을 위한 source domain으로 사용하였습니다.

4. Implements

Sentence embedding과 label name을 위하여 PLM model인 Electra small 과 BERT-Base 의 average token embedding을 사용했습니다. 또한, embedding trick으로 Pairs-Wise Embedding과 Gradual Unfreezing을 사용했습니다. Adam optimizer을 사용했으며 batch size는 4, learning rate은 1e-5로 설정했습니다. (1)에서 α\alpha 값은 0.3이고, (2)의 β\beta는 label name 과 support-set size에 따라서 {0.1, 0.5, 0.9} 중 하나의 값을 갖도록 했습니다. Kernel regression을 위한 MLP에서는 ReLU를 activation function으로 사용했고, layer의 hidden dim은 {5, 10, 20}으로 설정했습니다.

5. Baseline

논문에서 제안한 model의 성능을 평가하기 위하여 fine-tune based transfer learning method (TransferM), similarity-based FSL methods (MPN, MMN)과 비교하였습니다.

6. Main Results

업로드중..

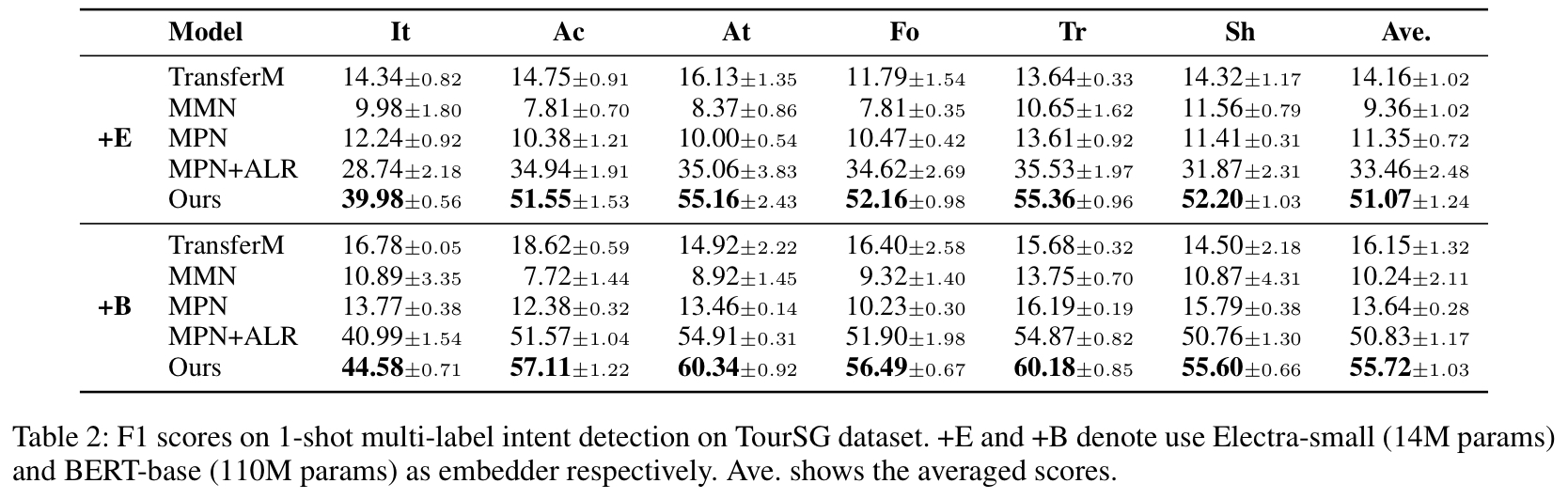
논문에서 제안한 모델이 baseline보다 전반적으로 성능이 좋았다.

Conclusion

  • Multi-lbael 환경에서 intent detection을 위한 few-shot learning 방법 연구
  • Meta Calibrated Threshold
    사전 지식과 domain 지식을 활용하여 적은 수의 support example로 threshold 추정
  • Anchored Label Representation
    Few-shot 환경에서 label-instance relevance score를 계산하기 위해 label representation이 서로 잘 구분되도록 함
  • Meta Calibrated Threshold와 Anchored Label Representation이 few-shot multi-label intent detection의 성능을 개선할 수 있는 것을 실험을 통해 증명
profile
LEE HANBIN
이전 포스트

Improving BERT Fine-Tuning via Self-Ensemble and Self-Distillation

다음 포스트

GraphSAGE : Inductive Representation Learning on Large Graphs

0개의 댓글