Radix Sort

현재까지는 분할, 정복에 해당하는 정렬 방식에 대해 배웠습니다. 이번에는 완전히 다른 방식의 정렬에 대해 배워보려고 합니다. 그것은 바로 Radix Sort입니다.

Radix Sort는 기수 정렬이라고 불립니다. 이번에도 visualgo 사이트로 직접 들어가서 보시면 이해에 큰 도움이 될 수 있습니다. 기수를 이용해서 정렬을 진행하는 방식이라고 생각하시면 쉽게 이해할 수 있는 알고리즘입니다.

Radix Sort에 대한 개념은 유튜브에는 잘 나와있지 않아서 여러 블로그 글을 참고하였습니다. 특히, 노마드 프로그래머님의 글을 참고하였으니 더욱 자세히 알고 싶으신 분은 꼭 확인 부탁드리겠습니다.

당연하게도 기수 정렬도 이해하기 쉬운 개념은 아닙니다. 코드로 나타내는 것 또한 어려운 부분이니 시간을 두고 천천히 공부하시기를 꼭 말씀드리고 본격적으로 알아보도록 하겠습니다.

---

1. Radix Sort

기수 정렬은 지금까지 배운 다른 정렬과 달리 서로의 배열 대상과 비교를 하지 않습니다. 이 부분이 기수 정렬의 가장 큰 차이점이라고 할 수 있습니다. 그렇다면, 기수 정렬은 어떠한 방식으로 정렬이 진행되는지 예를 들어 살펴봅시다.

[3, 54, 7, 6103, 1045, 365, 356]

위의 배열을 지수 정렬을 통해 정렬을 진행해볼까요?

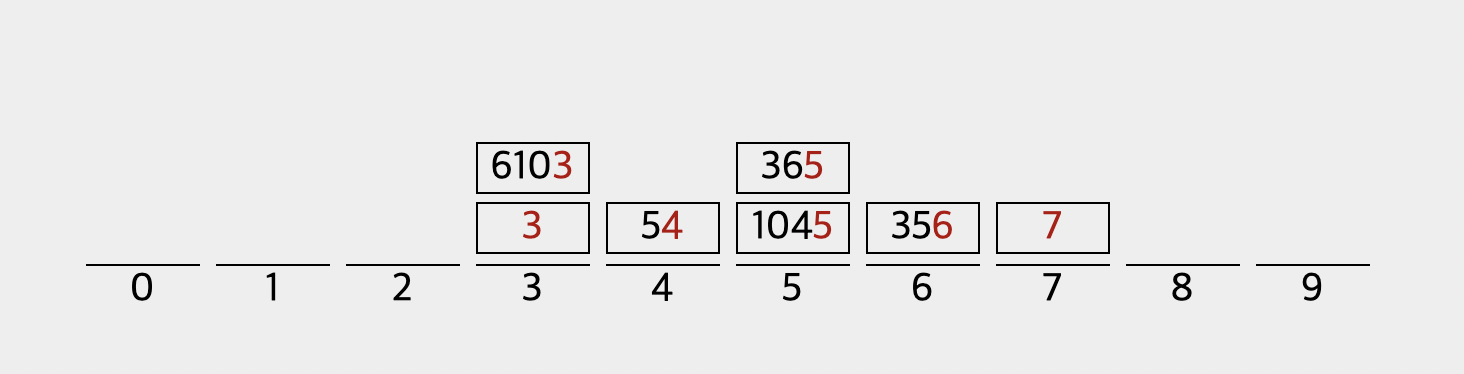
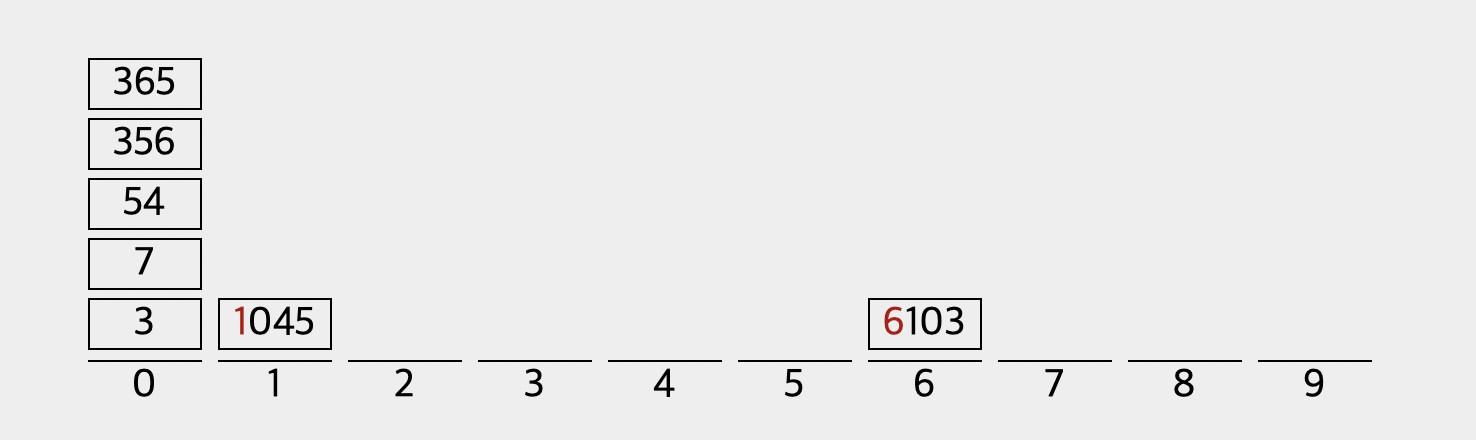
바로 이처럼 가장 뒤의 숫자인 1의 자리 숫자를 0부터 9까지 숫자별로 나누어 놓습니다. 그렇다면, 그 다음에는 어떻게 될지 예상이 되실까요?

[3, 6103, 54, 1045, 365, 356, 7]

이후 배열을 위의 그림에서 정렬한 방식대로 새롭게 배열을 만들어줍니다. 그리고 다음에는 자연스럽게 10의 자리 숫자를 분류하게 됩니다.

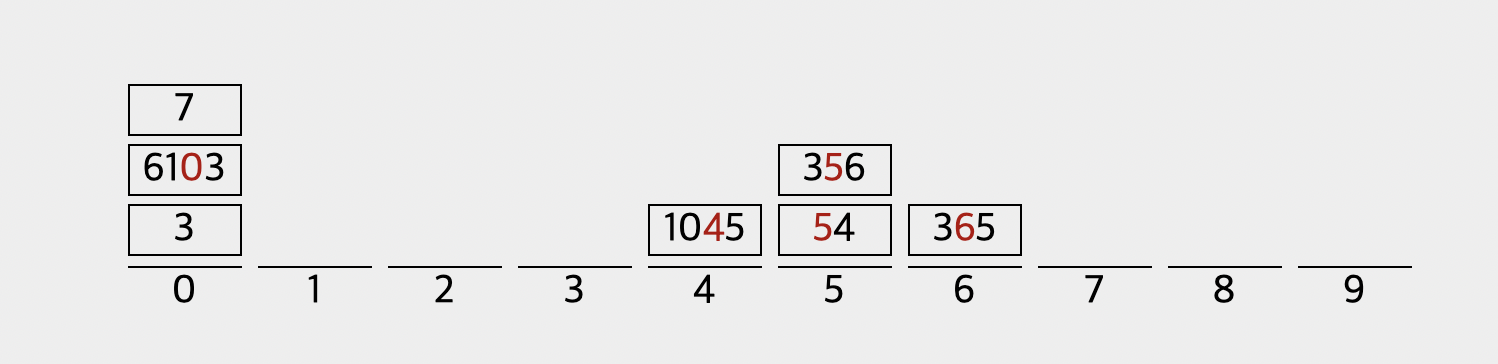
이처럼 10의 자리 숫자가 정렬이 진행된 것을 확인할 수 있습니다. 그러나 여기서 중요한 점은 3, 7과 같은 10의 자리가 없는 숫자는 어떻게 되었나요? 바로 0이라는 숫자로 분류가 되어있습니다.

[3, 6103, 7, 1045, 54, 356, 365]

이후에는 위와 같은 배열로 정리되게 됩니다. 다음에는 100의 자리가 되겠네요. 한 번 직접 예상을 해보시면 어떨까요?

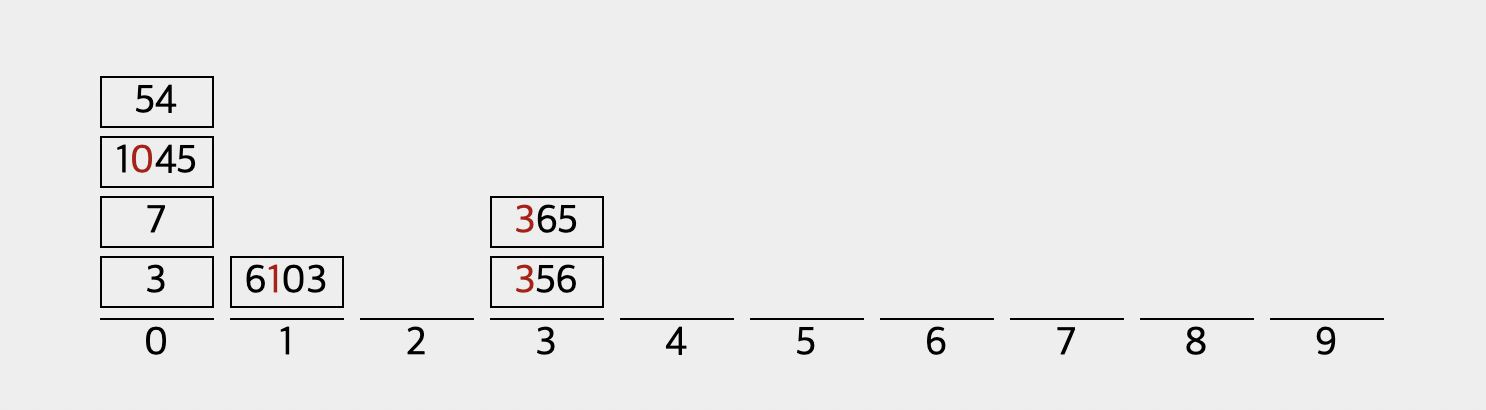
[3, 7, 1045, 54, 6103, 356, 365]

이제 서서히 정렬이 되어가는 것이 직접 눈에 보이시지 않나요? 이제 마지막인 1000의 자리로 넘어가보도록 하겠습니다.

[3, 7, 54, 356, 365, 1045, 6103]

이제 가장 큰 숫자가 1000의 자리로 이루어졌고, 이를 분류하였더니 배열의 정렬이 위처럼 완료된 것을 확인하실 수 있습니다. 그렇다면, 본격적으로 Radix Sort를 코드로 구현시켜보도록 하겠습니다. 😎

---

1.1 getDigit

getDigit(12345, 0); // 5
getDigit(12345, 1); // 4
getDigit(12345, 2); // 3
getDigit(12345, 3); // 2
getDigit(12345, 4); // 1
getDigit(12345, 5); // 0

기수 정렬에서 가장 첫 번째 해야할 일은 각 자리의 숫자에 해당하는 숫자가 무엇인지를 알아내는 함수를 정의해야 합니다. 12345라는 숫자가 뒤에서 0번째, 1번째, 2번째 등등에 해당하는 숫자를 파악할 수 있어야 분류가 가능해지기 때문입니다.

function getDigit(num, i) {
  return Math.floor(Math.abs(num) / Math.pow(10, i)) % 10;
}

위의 코드는 위에 나온 예시를 구하는 함수입니다. 그냥 무작정 이해하려해도 상관 없으며, 기수 정렬에서 중요한 내용은 아니기 때문에 가볍게 알고 지나치셔도 괜찮습니다.

그래도 예를 들어, 살펴보면 좋겠죠? getDigit(12345, 3)을 알아보도록 합시다. 먼저, Math.abs(num)는 절대값을 구하는 함수이므로 12345가 되겠습니다. 그리고 Math.pow(10, i)는 10에 i를 제곱한 값을 반환합니다. 여기서 i는 3이므로 1000이 되겠습니다.

그렇다면, 12345를 1000으로 나누어주면 12.345가 됩니다. 여기서 Math.floor(12.345)를 통해 12가 됩니다. 마지막으로, 12 % 10 = 2이므로 2가 나오게 됩니다.

굉장히 복잡한 로직이지만, 기수 정렬에서는 중요한 부분이 아니므로 가볍게 넘기셔도 됩니다. 이제 다음으로 숫자의 자릿수를 구하는 로직을 구현해봅시다.

---

1.2 digitCount

digitCount(1); // 1
digitCount(25); // 2
digitCount(314); // 3

이 코드는 숫자의 자릿수를 반환하는 코드가 되겠습니다. 간단하게 문자로 변환시켜서 이 길이를 반환시켜주면 되지 않을까요?

function digitCount(num) {
  return num.toString().length;
}

---

1.3 mostDigits

mostDigits([1234, 56, 7]); // 4
mostDigits([1, 1, 11111, 1]); // 5
mostDigits([12, 34, 56, 78]); // 2

이제 드디어 배열이 나왔네요. 자릿수에 해당하는 숫자를 구하고, 자릿수의 길이까지 구했습니다. 이번에는 배열 내에서 가장 자릿수가 가장 긴 숫자의 길이를 구해보도록 할까요?

function mostDigits(nums) {
  let maxDigits = 0;
  for (let i = 0; i < nums.length; i++) {
    maxDigits = Math.max(maxDigits, digitCount(nums[i]));
  }
  return maxDigits;
}

가장 긴 숫자의 길이를 구하는 것이기 때문에 digitCount 함수가 필요할 것 같습니다. 그리고 반복문을 통해 가장 큰 숫자의 길이에와 배열의 다음 숫자를 Math.max로 비교해주면 됩니다. 어려운 내용은 아니라 생각합니다.

이제 마지막으로 위에서 정의한 3가지의 함수를 통해 가장 중요한 기수 정렬에 대해 코딩을 진행해보도록 합시다. 여기서부터 갑자기 어려워지니 정신줄 똑바로 붙잡으시기 바랍니다! 🤦‍♂️

---

1.4 radixSort

radixSort([3, 54, 7, 6103, 1045, 365, 356])

function radixSort(nums) {
  const maxDigits = mostDigits(nums);

  for (let k = 0; k < maxDigits; k++) {
    let digitBuckets = Array.from({ length: 10 }, () => []);
    for (let i = 0; i < nums.length; i++) {
      let digit = getDigit(nums[i], k);
      digitBuckets[digit].push(nums[i]);
    }
    nums = [].concat(...digitBuckets);
  }
  return nums;
}

기수 정렬의 완전한 코드는 위와 같습니다. 그렇다면 처음부터 한 단계씩 알아보도록 하겠습니다.

const maxDigits = mostDigits(arr);

mostDigits는 배열의 숫자 중에서 가장 큰 숫자의 길이를 반환하는 함수였습니다. 이를 변수 maxDigits에 저장합니다. 그렇다면, 위에서 반환된 숫자만큼 반복을 진행하면 되는 것을 알게 되었습니다.

이후에는 각각의 자릿수에 해당하는 숫자를 담을 그릇을 만들어야합니다. 위의 그림에서 보셨던 것처럼 해당하는 자릿수에 따라 0~9까지의 숫자에 해당하는 그릇에 넣어서 분류를 진행해야 하기 때문입니다.

for (let k = 0; k < maxDigits; k++) {
  let digitBuckets = Array.from({ length: 10 }, () => []);
}

먼저, 위 코드는 저도 난생 처음 보게 된 코드입니다만, Array.from은 그래도 익숙하시리라 생각합니다. 유사 배열 객체를 만드는 코드이며, 길이가 10인 것을 만들게 되겠습니다.

이후 () => [] 내용은 단순히 이것 없이 Array.from({ length: 10 }로 끝나면, 배열에는 undefined 10개로만 구성이 되지만 위의 코드를 덧붙여서 아래와 같이 빈 배열로만 이루어지도록 만들 수 있습니다.

이제는 예상이 가시겠지만, 반복문을 통하여 각각의 배열 내로 숫자를 들어가게 해주면 되겠습니다.

for (let i = 0; i < nums.length; i++) {
  let digit = getDigit(nums[i], k);
  digitBuckets[digit].push(nums[i]);
}

radixSort([3, 54, 7, 6103, 1045, 365, 356])

예를 통해 위 코드를 이해해봅시다. digit은 변수로써 getDigit이라는 함수, 숫자에서 k에 들어가는 숫자를 찾아내서 이를 저장합니다.

k가 0이라면 1의 자리이므로, 3은 3, 54는 4, 6103은 3, 356은 6으로 분류되어 들어가게 되는 것이죠. 자릿수에 맞는 숫자를 push라는 메소드를 통해 배열로 넣는 것입니다.

위와 같은 과정을 통해 우리는 드디어 4단계를 거쳐 위의 그림에서 본 것과 같이 분류를 하게 되었습니다. 그럼 마지막 남은 것은 이를 순서대로 정렬하는 것일 겁니다.

nums = [].concat(...digitBuckets);

이제 0~9까지 배열로 나눠 들어있던 값을 합쳐서 배열로 만들어야합니다. 단순히 concat만 사용해서는 [[1],[3],[4]]의 형태가 되므로 이 앞에 전개 연산자(...)를 사용해주어야하므로 위와 같은 코드가 나오게 됩니다.

이렇게 쉽지 않은 기수 정렬을 코드로 구현해보았습니다. 현재까지 배웠던 정렬 중에 가장 복잡한 정렬이 아니었나 싶습니다. 이번 순서는 예상하셨다시피 기수 정렬의 Big O Notation을 살펴보도록 하겠습니다.

1.5 Big O Notation

종류	(BEST) 시간 복잡도	(Average) 시간 복잡도	(WORST) 시간 복잡도	공간 복잡도
Radix	O(nk)	O(nk)	O(nk)	O(n+k)

기수 정렬의 시간 복잡도는 위와 같이 계산할 수 있습니다. 기수 정렬의 Big O의 경우 논쟁의 여지가 있지만, 현재까지 일반적으로 알려진 것에 대해 알려드리겠습니다.

기수 정렬의 시간 복잡도인 O(nk)에서 n은 배열 내에 있는 숫자들의 개수(배열의 길이)입니다. 그리고 k는 그 숫자들의 길이(평균)를 의미합니다.

이론적으로, 기수 정렬이 숫자를 서로 비교하는 정렬보다 빠르다고 하지만 컴퓨터가 메모리에 얼마나 큰 숫자를 저장할 수 있느냐에 따라 다를 수 있습니다. 하지만 서로의 숫자를 비교하지 않고 숫자의 특성을 이용한 정렬이라니 매우 재밌는 정렬 방법이라고 할 수 있겠습니다.

여기까지가 다소 복잡하지만 재밌는 기수 정렬에 대해 알아봤습니다. 아래에는 제가 이번 기수 정렬과 단일 연결 리스트를 공부하며 또 다시 한번 프로그래밍의 벽에 마주하여 힘든 시간을 보냈지만, 의욕을 얻게 된 영상에 대해 소개해드리도록 하겠습니다.

---

최근 유튜브에서 우연히 보았던 영상이 있다. 처음 프로그래밍 공부를 할 때 어려운 것과 가장 효율적인 공부 방법이라는 라매개발자라는 유튜버의 영상이었다.

영상을 보고 깨달은 부분이 굉장히 많았기 때문에 반드시 시청하시기를 권해드리고, 그래서 가장 효율적인 공부 방법이 뭔데? 라고 물으신다면, 정답은🤓

요구사항을 구체적이고 절차적으로 변환하는 능력을 키우자

라는 말이었습니다. 최근 알고리즘과 자료구조를 공부하면서 비전공자로서 처음 공부하는 것이기 때문에 당연히 100%를 흡수하는 것은 큰 욕심이라는 것을 알면서도 며칠이 지나면 로직 조차도 까먹는 저의 모습을 보며, 큰 절망에 빠지고 있습니다.

위 강의를 보고 느낀 것은 내가 100% 온전히 코드를 외우는 것은 불가능하니 퀵 정렬, 병합 정렬 등에서 어떠한 절차를 통해 코드가 이루어지며 이를 구체적으로 변환하는 능력을 점차적으로 키워야한다는 것입니다.

본격적으로 기수 정렬에 대해 알아보면서, 위의 내용을 참고하시면서 어떠한 절차로 코드가 진행이 되고 완벽하게 까지는 아니더라도 처음에는 어느 정도만 구체적으로 변환시킬 수 있다면 그것으로 만족하고, 이후에 반복해서 학습을 하시면 어느새 그 능력이 자연히 성장하리라 확신합니다.