Quick Sort

이번에는 병합 정렬에 이어 다른 획기적인 정렬 방법, 바로 그 유명한 퀵 정렬을 자바스크립트 코드로 알아보도록 하겠습니다.

Quick Sort는 말 그대로 빠른 정렬이라고 할 수 있습니다. 이번에도 visualgo 사이트로 직접 들어가서 보시면 이해에 큰 도움이 될 수 있습니다. 그러나 퀵 정렬은 한 번을 봐서는 이해하기가 다소 어려운 개념입니다.

그래서 이번에도 Merge Sort에 이어 JavaScript 코드는 아니지만, 유튜버 코딩하는거니님의 퀵 정렬 설명을 영상으로 확인해보시면, 더욱 쉽게 이해하실 수 있습니다.

퀵 정렬은 한 번에 이해하시지 못해도 괜찮습니다. 여러 번에 걸쳐 코드를 반복해서 이해하고 작성해보는 연습이 필요한 정렬 방법이니 시간을 들여야 한다는 잊지 마시기 바랍니다! 그럼 본격적으로 퀵 정렬에 대해 살펴봅시다.

1. Quick Sort

---

퀵 정렬은 병합 정렬과 같이 분할 정복 방식입니다. 퀵 정렬을 크게 놓고 보면, 피벗을 정한 뒤 피벗의 위치를 확정해가며 정렬하는 방법이라고 할 수 있습니다.

퀵 정렬의 핵심은 결국 이 피벗(pivot)이라고 할 수 있습니다. 피벗의 사전적인 의미는 쉽게 말해 회전하는 축을 의미합니다. 아직 이해가 안되시는 분은 미드 프렌즈의 영상을 보고 오시면 쉽게 이해하실 수 있습니다. 아주 재미있는 영상이니 꼭 보시길 추천드리겠습니다🤣

[4, 8, 2, 1, 5, 7, 6, 3]

이번에도 예를 들어서 살펴보도록 하겠습니다. 위의 배열을 퀵 정렬을 통해 정렬을 진행한다고 가정해봅시다. 먼저 위에서 언급한 피벗을 정해줘야 합니다. 이 피벗에 따라 퀵 정렬의 속도가 달라지므로 매우 중요하다고 할 수 있습니다. 그렇다면 피벗은 어떻게 정하는 것일까요?

주로, 가장 왼쪽, 오른쪽, 그리고 가운데를 정하는 방법이 있습니다. 그러나 최악의 경우에는 시간 복잡도가 O(n²)이 될 수 있기 때문에 이를 위해 평균적인 퀵 정렬의 속도를 보일 수 있도록 피벗을 랜덤으로 정하는 방법도 있습니다.

이 피벗의 선정에 있어서는 아직도 다양한 연구와 논문이 진행되고 있다고 합니다. 먼저, 퀵 정렬이 어떻게 진행되는지 예를 들어서 살펴보도록 하겠습니다. 저희는 피벗은 가장 첫 번째 값으로 코드를 진행하겠습니다.

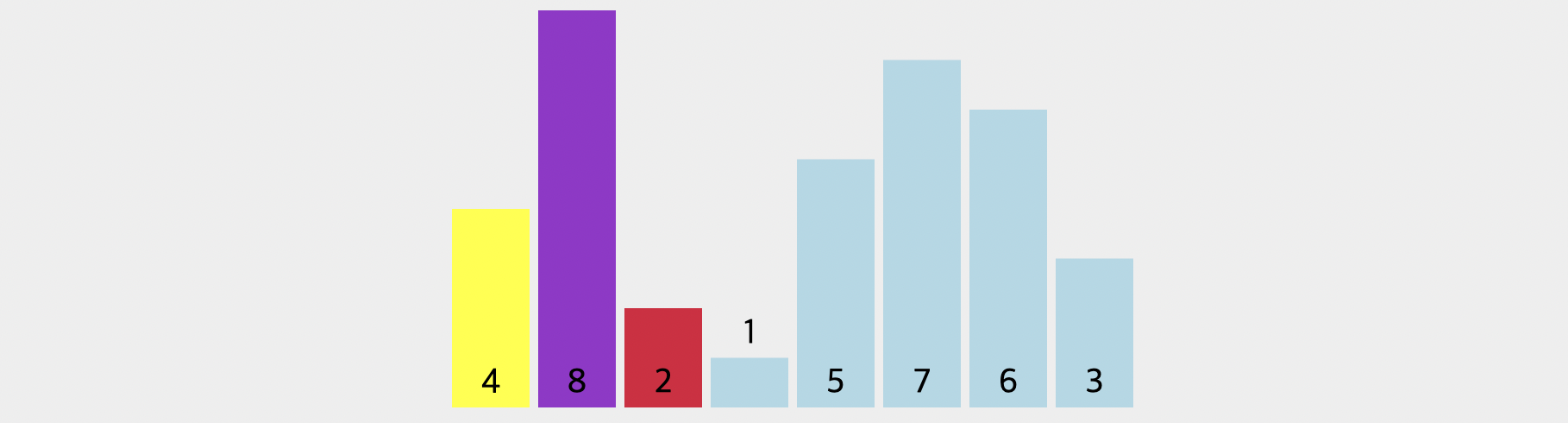
위의 그림에서 노란색으로 표시된 가장 첫번째 값이 바로 피벗입니다. 그리고 배열의 두번째부터 반복을 시작해서 피벗보다 작은 값을 찾도록 합니다. 8은 피벗값(4)보다 크므로 넘어갑니다. 그리고 드디어 배열의 세번째 값에서 4보다 작은 수를 찾아냈습니다.

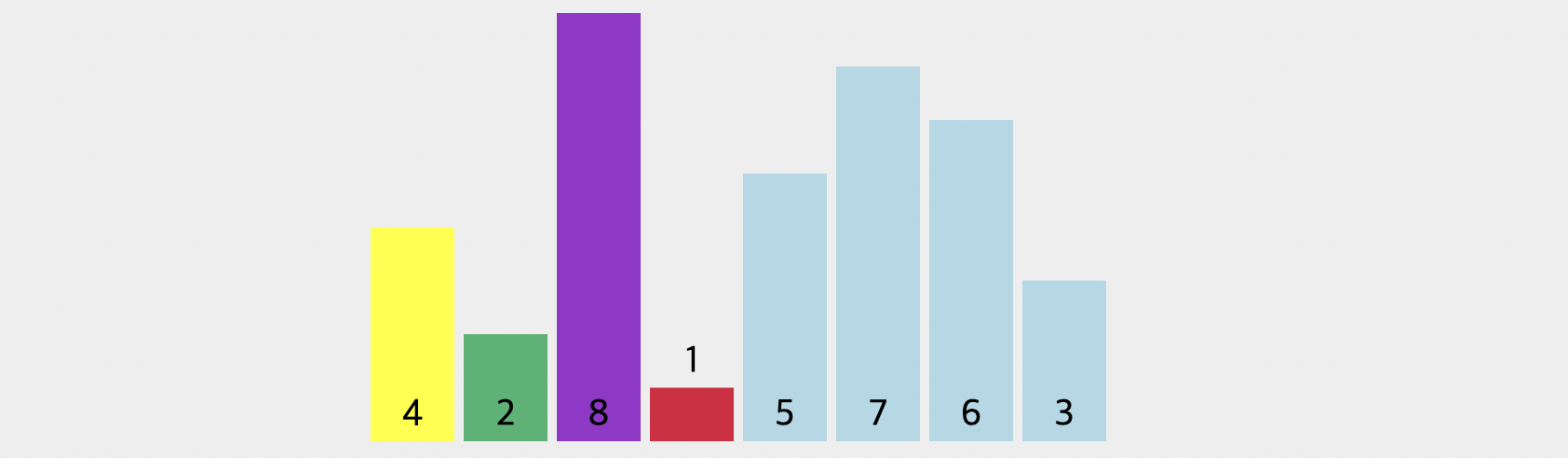
그렇다면 어떻게 될까요? 바로 위의 그림과 같이 2와 8의 값을 바꿔줍니다. 그리고 중요한 것은 바꿔둔 값을 기억해야한다는 점입니다. 왜냐하면 위처럼 또 피벗보다 작은 값을 찾게 된다면, 이를 또 바꿔줘야하 하기 때문입니다. 그럼 이 같은 경우에는 어떤 값을 서로 바꿔줘야 할까요?

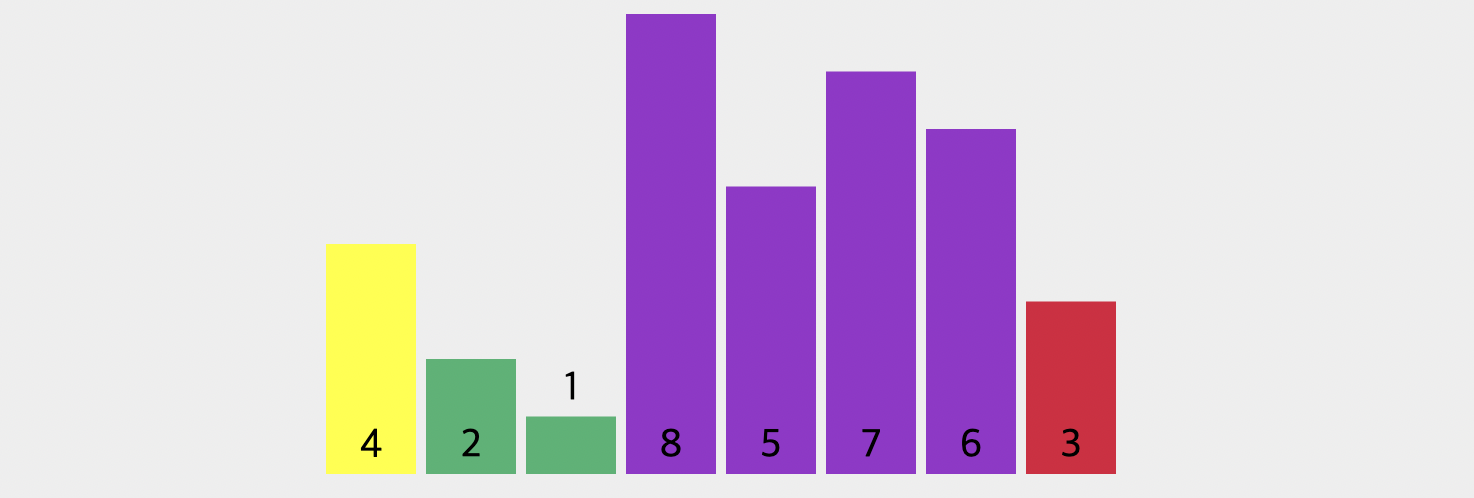
그렇습니다. 바로 1과 8을 바꿔줘야 합니다. 위의 그림처럼 서로를 바꿔주었고 이제 배열의 마지막 순서인 3까지 오게 되었습니다. 3 또한 피벗값(4)보다 작기 때문에 8과 자리가 바꿔지게 되겠네요.

[4, 2, 1, 8, 5, 7, 6, 3]
[4, 2, 1, 3, 5, 7, 6, 8]

자, 이처럼 배열을 모두 돌아 위와 같은 배열이 완성되었습니다. 하지만 여기서 끝나지 않습니다. 왜냐하면, 피벗을 정확한 위치로 이동시켜줘야 하기 때문입니다. 피벗보다 작은 수를 왼쪽으로 모아놨으니 피벗값은 그보다 한칸 뒤로 가야되겠죠?

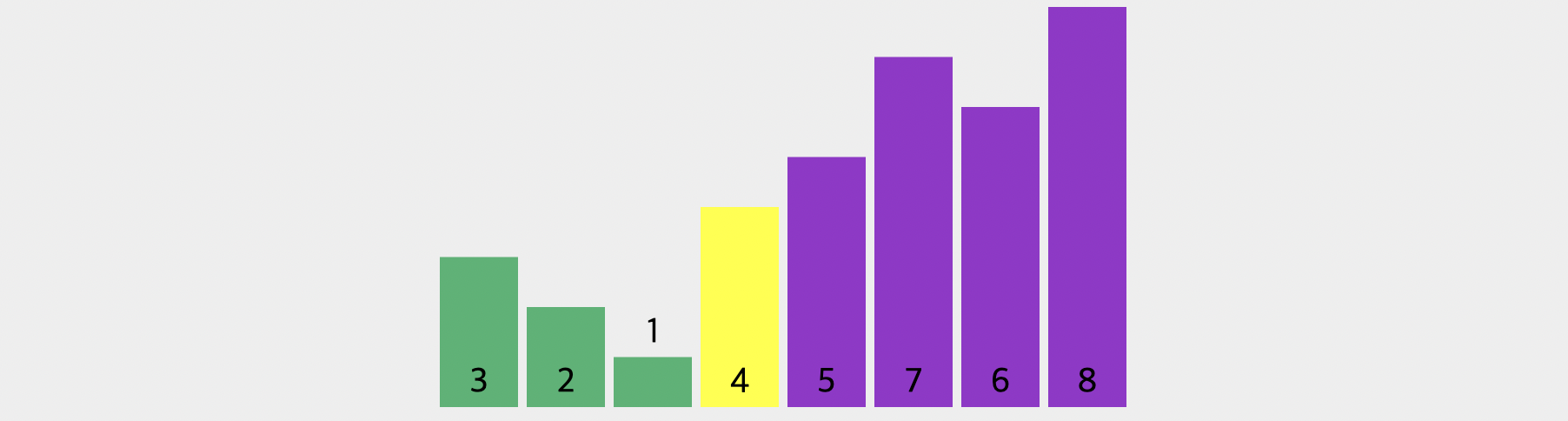
그래서 이렇게 3과 4의 자리를 바꿔주는 것입니다. 이는 피벗의 위치와 3이라는 값이 있던 위치를 기억해둬야 가능한 방법일 것입니다. 이제 피벗이었던 4를 기준으로 작은 값들과 큰 값들로 배열이 두 부분으로 나눠졌네요. 이제 다음부터는 어떻게 되는 것일까요?

[3, 2, 1, 4, 5, 7, 6, 8]
left  p-1 p p+1      right

예상하신 것처럼 피벗을 기준으로 왼쪽에서 피벗 전까지, 그리고 피벗 다음부터 오른쪽까지를 재귀함수로 진행해주면 됩니다. 이때문에 병합 정렬에서 배웠던 Divide & Conquer 즉, 분할 정복 방식이라고 할 수 있는 것입니다.

다만, 여기서 재귀함수의 base code는 쉽게 if (left < right)로 왼쪽 값보다 오른쪽 값이 작을 때까지 정렬을 진행하면 됩니다. 이제는 코드를 직접 작성하며 알아보도록 합시다.

1.1 pivot

---

function pivot(arr, start = 0, end = arr.length) {
  const swap = (arr, idx1, idx2) => {
    [arr[idx1], arr[idx2]] = [arr[idx2], [arr[idx1]];
  };
  
  let pivot = arr[start];
  let swapIdx = start;
  
  for (let i = start + 1; i <= end; i++) {
    if (pivot > arr[i]) {
      swapIdx++;
      swap(arr, swapIdx, i);
    }
  }
  swap(arr, start, swapIdx);
  return swapIdx;
}

가장 먼저 function pivot(arr, start = 0, end = arr.length)으로 매개변수에 기본값을 정하여 진행합니다. 그리고 당연하게도 값을 바꿔주어야 하므로 이번에도 swap 함수를 명시해줍니다.

let pivot = arr[start];
let swapIdx = start;

그리고 본격적으로 피벗값을 정해줍니다. 저희는 첫 번째 값으로 정하기로 했기 때문에 arr[start]를 변수에 저장합니다. 그리고 다음으로 swapIdx라는 변수를 통해 start부터 시작하여 피벗값보다 작은 숫자의 index를 기억할 수 있도록 코드를 작성합니다.

for (let i = start + 1; i <= end; i++) {
  if (pivot > arr[i]) {
    swapIdx++;
    swap(arr, swapIdx, i);
  }
}

이제 반복문을 통해 실제로 피벗값보다 작은 값을 왼쪽으로 몰아주는 코드를 작성했습니다. i가 증가하면서 arr[i]가 피벗값보다 작다면, 바꿔주면 됩니다. 그러나 무엇과 바꿔주어야하는 것일까요?

여기서 swapIdx가 등장합니다. 그럼 바로 반복문이 증가하면서 피벗보다 작은 값인 2를 만났을 때를 알아봅시다. 예를 보면서 살펴봅시다.

[4, 8, 2, 1, 5, 7, 6, 3]
 p     i
// 현재 swapIndex = start이지만, 피벗값(4)이 아닌 8과 바꿔줘야하므로 1을 증가
swapIndex++; // swapIndex = 1
swap(arr, swapIdx, i); // arr[swapIndex]와 arr[i]를 바꿔주면 완료! 

코드는 위와 같이 진행이 됩니다. 하지만, 여기서 끝이 나면 안됩니다. 반복문이 끝나면 배열은 [4, 2, 1, 3, 5, 7, 6, 8] 이렇게 바뀌게 됩니다. 여기서 필요한 것은 무엇일까요? 바로 이전에 말했던 마지막으로 피벗과 3을 바꾸는 것입니다.

swap(arr, start, swapIdx);
return swapIdx;

이처럼 swap 함수를 실행해주고 마지막으로 swapIndex를 리턴해주면 끝이 납니다. [3, 2, 1, 4, 5, 7, 6, 8]으로 끝이 나게 되고,swapIndex는 피벗값의 자리였던 3이 되는 것을 꼭 이해하실 수 있어야합니다.

이제 피벗을 기준으로 왼쪽에서 피벗 전까지, 그리고 피벗 다음부터 오른쪽까지를 재귀함수로 진행하는 코드를 작성해주면 됩니다.

1.2 quickSort

function quickSort(arr, left = 0, right = arr.length - 1) {
  if (left < right) {
    let pivotIndex = pivot(arr, left, right);
    // left
    quickSort(arr, left, pivotIndex - 1);
    // right
    quickSort(arr, pivotIndex + 1, right);
  }
  return arr;
}

이처럼 if (left < right)를 조건으로 재귀함수가 실행되게 해줍니다. 처음 left, right의 기본값은 0과 arr.length - 1로 정해줍니다.

그리고 이후에는 pivotIndex 값이 나오므로 이 값을 기준으로 왼쪽과 오른쪽을 나누어서 정렬을 진행하면 됩니다.

// left
quickSort(arr, left, pivotIndex - 1);
// right
quickSort(arr, pivotIndex + 1, right);

이처럼 두 개로 나누어서 정렬을 진행하고 마지막으로 배열을 반환하면, 퀵 정렬이 완료됩니다. 퀵 정렬은 위에서 언급했던 것처럼 한 번에 이해하기 어려운 알고리즘 개념이기 때문에 여러 번 보고 코드를 작성하는 방법으로 익숙해져야 합니다.

그러면, 퀵 정렬의 Big O Notation에 대해 알아봅시다.

1.3 Big O Notation

종류	(BEST) 시간 복잡도	(Average) 시간 복잡도	(WORST) 시간 복잡도	공간 복잡도
Quick	O(n log n)	O(n log n)	O(n²)	O(n)

퀵 정렬의 시간 복잡도는 위와 같이 계산할 수 있습니다. 평균은 n log n으로 분할, 정복 방식인 병합 정렬과 같은 것을 보실 수 있습니다.

[8, 5, 6, 1, 3, 7, 2, 4, 12, 13, 14, 11, 9, 15, 10]

먼저, BEST, 평균인 n log n을 위의 배열과 함께 분할과 정복 방식으로 이해해보도록 하겠습니다. 피벗은 가장 첫 번째 값을 기준으로 합니다.

• 분할 1단계

                     8
[4, 5, 6, 1, 3, 7, 2] [12, 13, 14, 11, 9, 15, 10]

• 분할 2단계

                     8
         4                     12
[2, 1, 3] [6, 7, 5] [10, 11, 9]  [14, 15, 13]

• 분할 3단계

                     8
         4                     12
    2         6           10        14
 1     3   5     7     9     11  13    15

이처럼 피벗을 정한 뒤 분할을 완료하고 왼쪽, 오른쪽으로 나누어 퀵 정렬을 진행하게 됩니다. 분할은 이처럼 시간 복잡도를 병합 정렬과 같이 O(log n)으로 계산할 수 있습니다.

그리고 정복은 각각의 단계에서 발생하게 되므로 여기에 n을 곱해주게 되는 것입니다. 이를 통해, 평균의 시간 복잡도는 n log n이 됩니다.

그렇다면, WORST인 O(n²)은 어떻게 되는 것일까요?

[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15]

위와 같이 미리 정렬이 완료된 예를 들어봅시다. 쉽게 예상이 되실 것이라 생각합니다.

• 분할 1단계

 1
   [2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15]

• 분할 2단계

 1
   2
     [3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15]

• 분할 3단계

 1
   2
     3
       [4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15]

이러한 식으로 진행이 되겠죠? 결국, 배열의 길이가 15라면 15단계의 분할 과정을 겪게 되고, 여기에 정복 과정인 15단계를 실행하게 됩니다. 결국, 이 둘을 곱한 값인 O(n²)이 최악의 시간 복잡도로 계산이 되는 것입니다.

이러한 이유로 퀵 정렬에서는 피벗값이 시간 복잡도에 영향을 끼치는 매우 중요한 요소라고 할 수 있습니다. 이렇게 미리 정렬된 배열의 위험을 피하기 위해 가장 첫번째 값을 피벗값으로 정하기보다 중간값이나 랜덤값으로 피벗값을 정하는 경우가 많다고 할 수 있겠습니다.

그러나 또 반대로 그 값이 배열의 최소값 또는 최대값이 될 수도 있으니 어떠한 경우가 최적의 피벗값인지에 대해 매우 많은 연구가 진행되고 있는 이유입니다.

여기까지가 다소 복잡하고 어려운 퀵 정렬에 대해 알아봤습니다. 절대 한 번에 이해하려하지 마시고 여러 번 개념을 잘 이해하고 숙지할 수 있도록 반복해서 학습해야한다는 점 잊지 마세요!🧑‍💻