Selection & Insertion Sort
이번에는 저번에 배운 버블 정렬에 이어 다른 두 가지 종류의 선택 정렬과 삽입 정렬에 대해 알아보겠습니다.
버블 정렬과 함께 세 종류의 정렬은 기본적인 정렬 방법으로 실제적으로 많이 사용되는 정렬은 아니지만, 이를 기본으로 추후 배우게 될 어려운 정렬의 기초가 되니 충분히 숙지가 될 수 있어야합니다. 이제부터 두 정렬에 대해 살펴봅시다.
이번에도 visualgo 사이트에서 두 가지 종류의 정렬에 대해 시각적으로 확인해보실 수 있으니 직접 들어가서 보시면 이해에 큰 도움이 됩니다.
1. Selection Sort
선택 정렬은 하나의 개념만 기억하면 되며, 이를 통해 정렬이 진행됩니다. 그 개념은 바로 최소값입니다. 루프를 진행하며 최소값을 찾아 단계를 진행해감에 따라 첫번째, 두번째, 그리고 세번째 배열 데이터와 swap을 진행하는 형태입니다.
버블 정렬이 마지막 배열 데이터부터 정렬이 완료되었다면, 선택 정렬은 반대로 처음의 배열 데이터부터 정렬이 완성되는 것이라 할 수 있습니다.
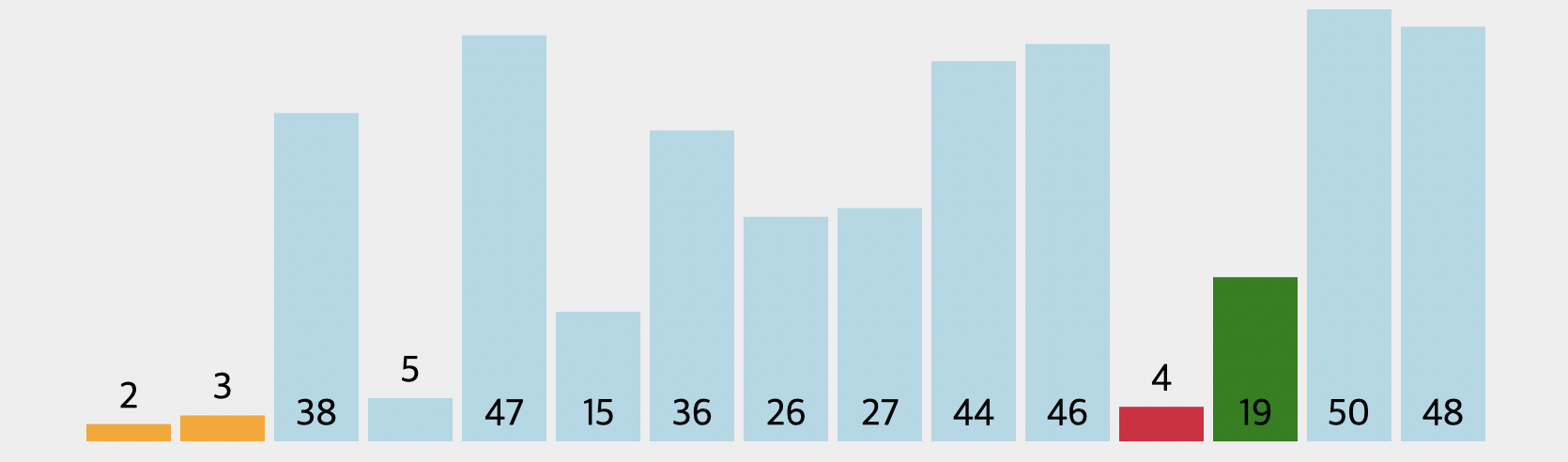
위의 그림을 통해 살펴보면, 앞의 노란색으로 표시된 두 숫자는 이미 정렬이 완료된 상태입니다. 3번째 단계로서 데이터를 탐색하면서 최소값을 찾아가는 과정을 보여줍니다.
빨간색으로 표시된 숫자 4는 현재까지의 최소값을 나타내며 초록색은 3번째 단계의 전 탐색 과정을 나타냅니다. 마지막 데이터인 48까지 탐색을 완료하지 않았으므로 컴퓨터는 아직까지는 4가 최소값이지만, 확실하게 모르는 상태라할 수 있습니다.
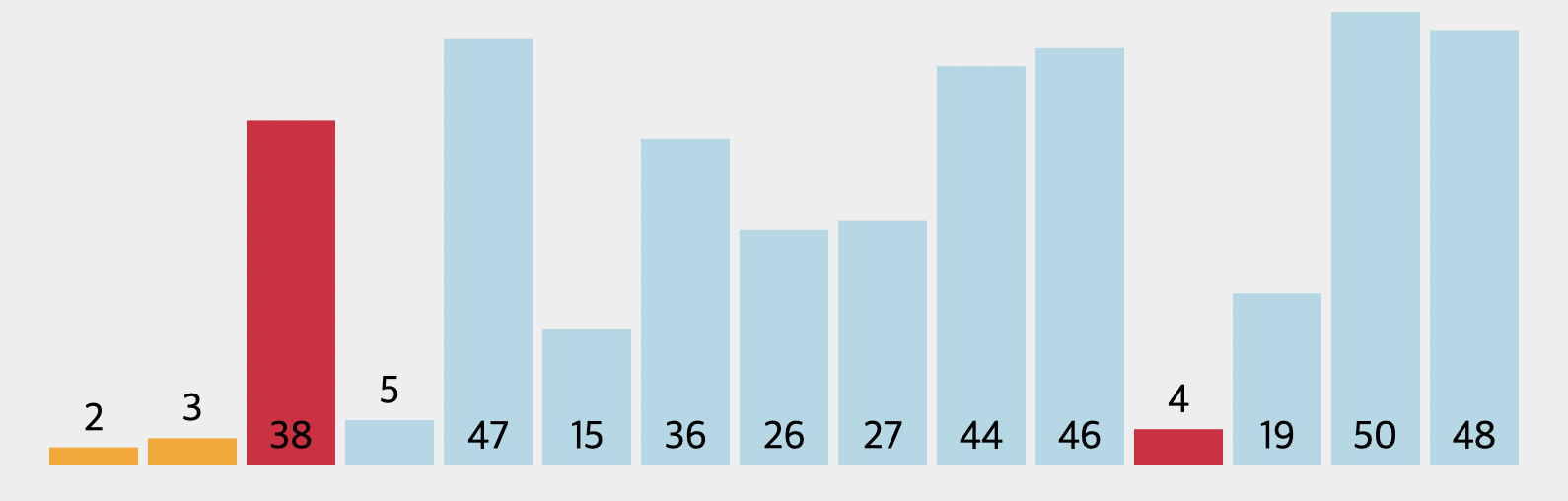
이제 마지막 데이터까지 탐색을 완료하였습니다. 컴퓨터는 4가 이번 단계에서 최소값임을 확인하였습니다. 이후 3번째의 배열 데이터를 선택하고 서로 swap을 진행하기 위해 준비합니다.
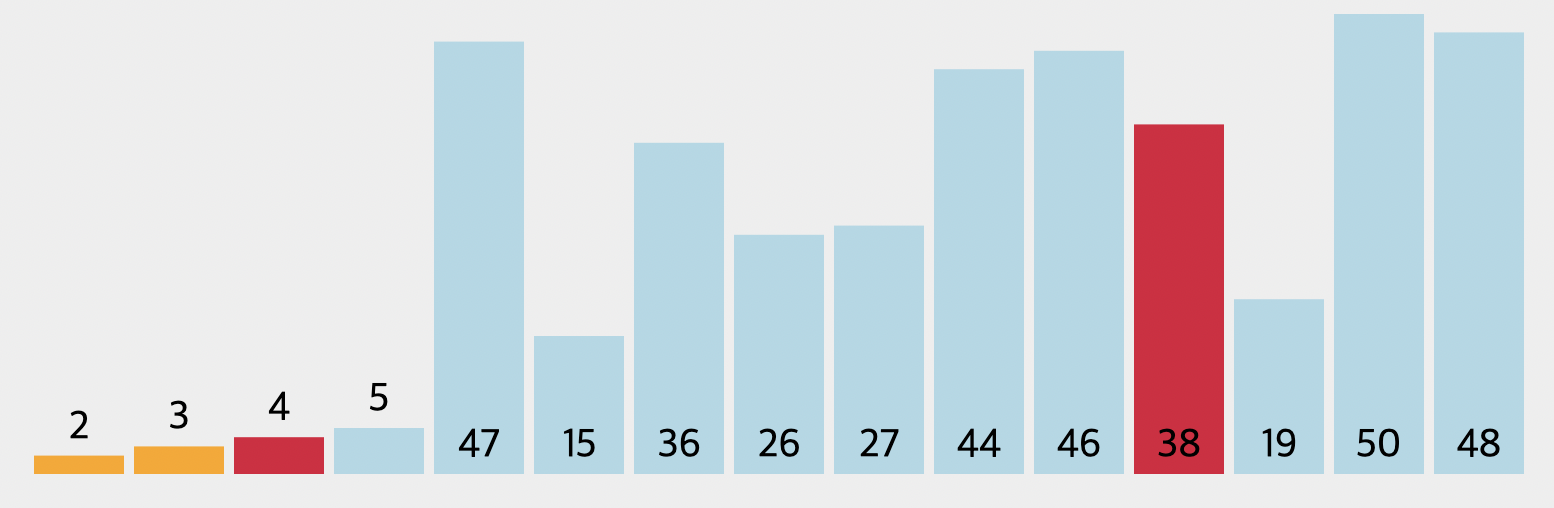
이렇게 swap을 진행하면 3단계의 선택 정렬이 완료된 것입니다. 이를 마지막 배열 데이터까지 탐색을 하게 되면 선택 정렬이 완료됩니다. 이를 코드로 구현해보도록 합시다.
selectionSort
function selectionSort(arr) {
const swap = (arr, idx1, idx2) => {
[arr[idx1], arr[idx2]] = [arr[idx2], arr[idx1]]
};
for (let i = 0; i < arr.length; i++) {
let min = i;
for (let j = i + 1; j < arr.length; j++) {
if (arr[j] < arr[min]) {
min = j;
}
}
if (i !== min) {
swap(arr, i, min);
}
}
return arr;
}버블 정렬과 마찬가지로 먼저 swap이라는 배열 데이터를 서로 바꾸는 함수를 실행합니다. 이후 본격적으로 선택 정렬에 대한 코드를 구현합니다.
선택 정렬에서 가장 중요한 개념은 최소값이라고 하였습니다. 그렇다면, 반복문을 진행하면서 최소값을 갱신하면서 마지막 단계에서는 두 데이터를 바꿔주면 됩니다. 이를 변수 i, j, min 3개의 데이터로 알아보겠습니다.
[34, 22, 10, 19, 27]
또한, 예를 들면 이해가 쉬우므로 위의 배열 데이터로 예를 들어보겠습니다.
| i | j | min |
|---|---|---|
| 0 | 1 | 0(초기값) ⇒ 1 |
| 0 | 2 | 1 ⇒ 2 |
| 0 | 3 | 2 |
| 0 | 4 | 2 |
먼저 1번째 단계부터 살펴보겠습니다. 최소값은 실제 값이 아닌 최소값에 해당하는 인덱스를 표기합니다. 그 이유는 그래야만 배열 데이터를 swap하기 용이하기 때문입니다.
첫 번째 단계에서 보시는 것처럼 첫 단계 i의 초기값이 0이며, let min = i이라는 코드를 통해 먼저 최소값에 초기값을 입력하도록 합니다. 이는 i가 증가하는 현재 상황에서 지속적으로 최소값을 단계에 따라 자동으로 갱신하는 역할을 합니다.
그리고 실제적으로 j를 통해 탐색을 진행합니다. 첫 번째 단계부터 34와 22를 비교하였을 때 0번째보다 1번째의 데이터가 작은 것을 확인할 수 있습니다.
if (arr[j] < arr[min]) {
min = j;
}이러한 경우, 위의 조건문이 실행되도록 합니다. 최소값이라는 변수에 j가 입력되면서 이제는 0이 아닌 1이 됩니다. i가 0인 단계를 모두 탐색하면 2번째에 있는 10이 최소값임이 확인됩니다. 이를 통해 min 변수에는 2가 입력이 되도록 합니다.
이후 swap을 통해 0과 2번째의 데이터를 바꿉니다. 이후에는 i = 1부터 진행하게 됩니다. 이를 표로 확인해보시죠.
| i | j | min | arr[min] | arr |
|---|---|---|---|---|
| 1 | 2 | 1 | 22 | [10, 22, 34, 19, 27] |
| 1 | 3 | 3 | 19 | [10, 22, 34, 19, 27] |
| 1 | 4 | 3 | 19 | [10, 19, 34, 22, 27] |
| 2 | 3 | 3 | 22 | [10, 19, 34, 22, 27] |
| 2 | 4 | 2 | 22 | [10, 19, 22, 34, 27] |
| 3 | 4 | 4 | 27 | [10, 19, 22, 27, 34] |
이처럼 선택 정렬을 진행하면서 최소값을 갱신하고 이를 i와 변경하면서 마지막에는 배열에 모두 정렬이 된 것을 확인할 수 있습니다. 어렵지 않게 이해하실 수 있으리라 생각합니다.
if (i !== min) {
swap(arr, i, min);
}그리고 추가적으로 위 코드를 마지막에 덧붙여주어 i가 최소값이라면 불필요하게 swap을 진행하지 않는 조건을 달아주도록 합니다. 지금까지 선택 정렬에 대해 알아봤으며, 이제는 삽입 정렬에 대해 살펴봅시다.
2. Insertion Sort
삽입 정렬은 말 그대로 삽입을 해주는 정렬입니다. 말로 들어서는 이해가 어려우므로 그림으로 이해해보죠.
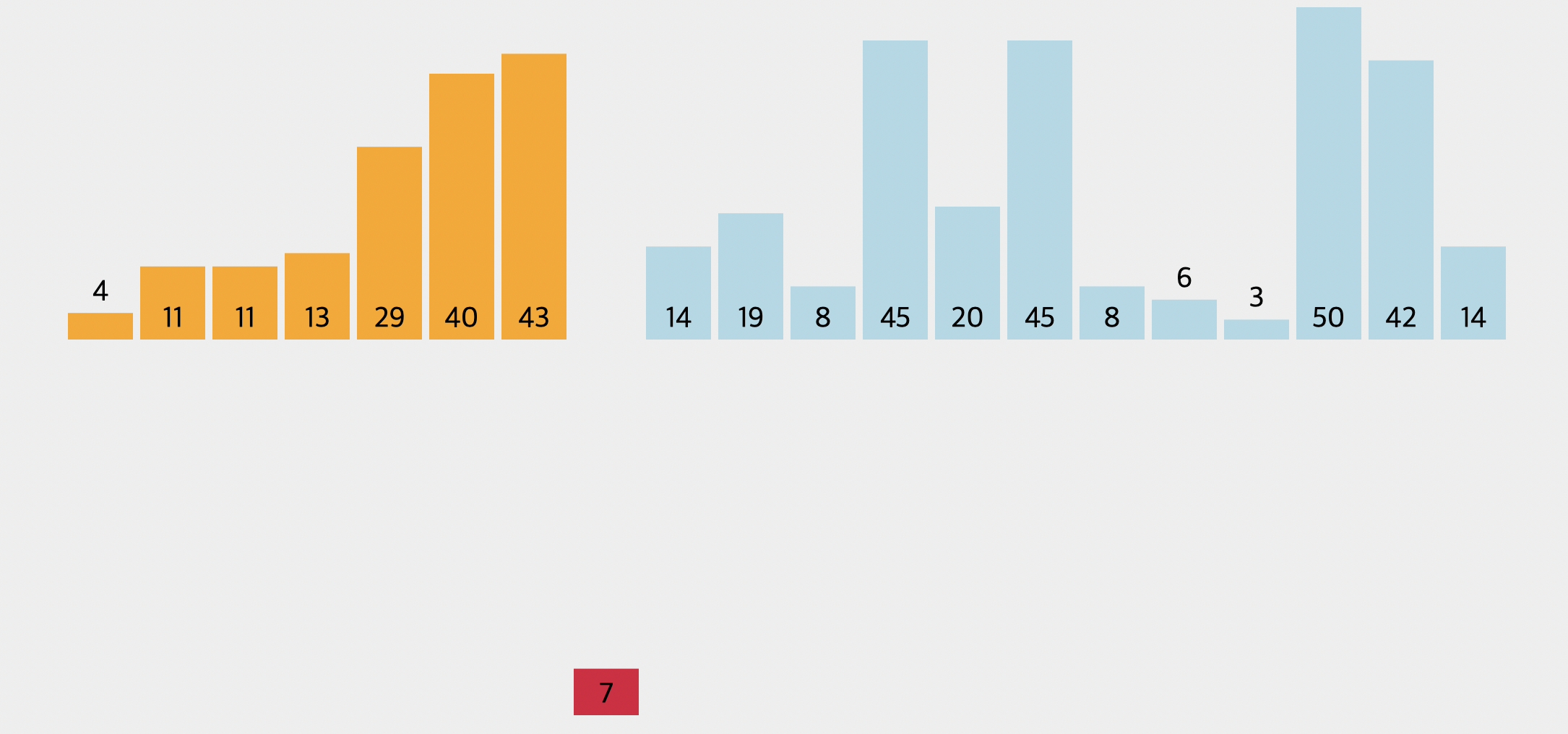
노란색으로 표시된 부분은 이미 정렬이 완료된 부분입니다. 그리고 이번 순서는 숫자 7이 됩니다. 보시는 것과 같이 숫자 7은 따로 떨어져나와 있으며, 정렬이 진행됨에 따라 본인의 자리를 찾아가야 되겠죠? 이렇게 삽입 정렬은 왼쪽부터 정렬이 진행이 되는 특징을 갖고 있습니다.
그렇다면 실제로 정렬은 어떻게 되는 것일까요? 숫자 7은 아시다시피 현재 맨 앞에 있는 숫자 4 뒤에 위치되어야만 정렬이 완료된다고 할 수 있습니다.
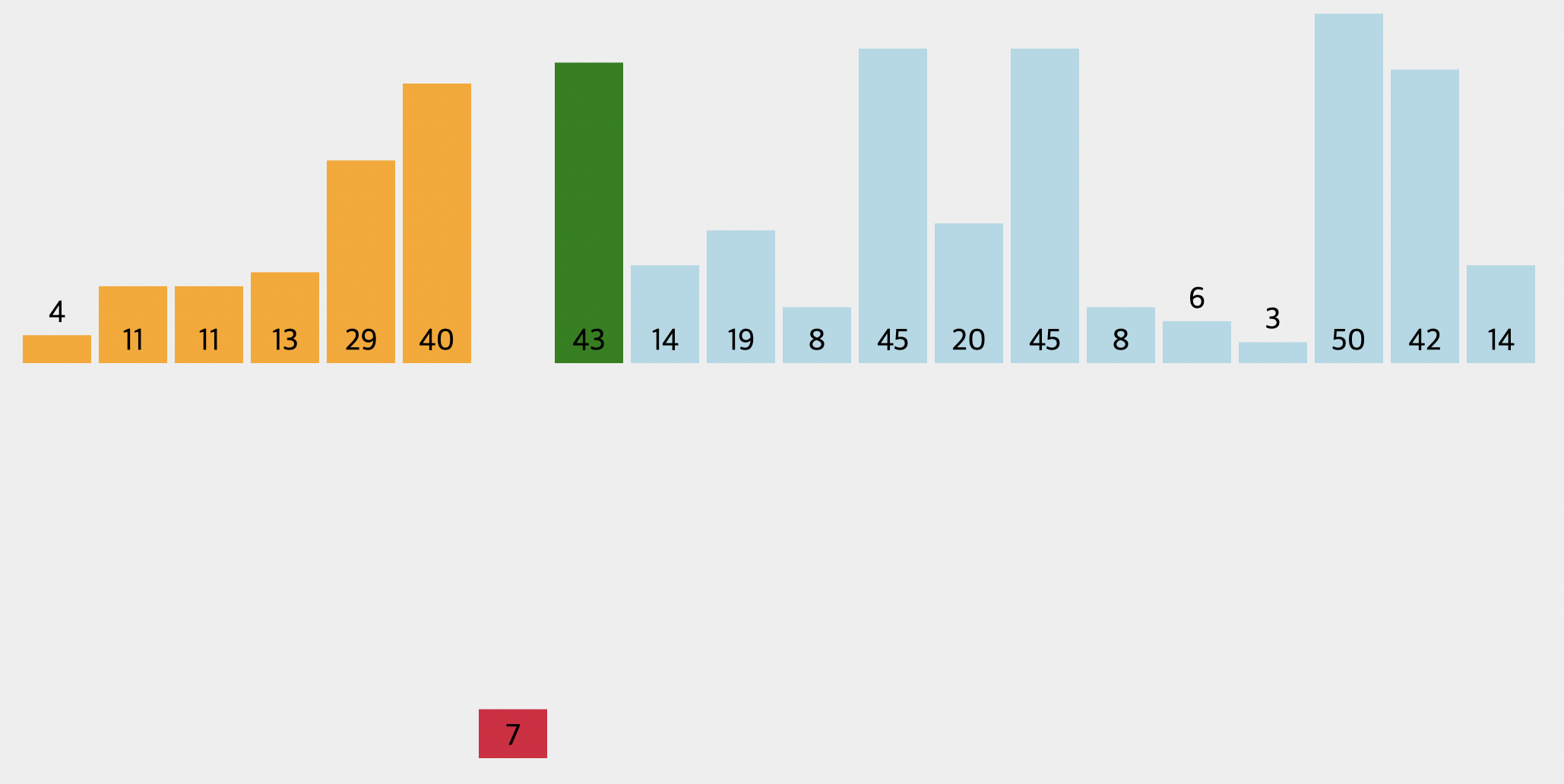
먼저 바로 왼쪽에 있는 43과 7을 비교합니다. 두 수를 비교하여 정렬하려는 숫자가 더 크다면 자리를 이동하지 않게 되고, 이 경우처럼 작다면 큰 숫자가 오른쪽으로 이동하게 됩니다.
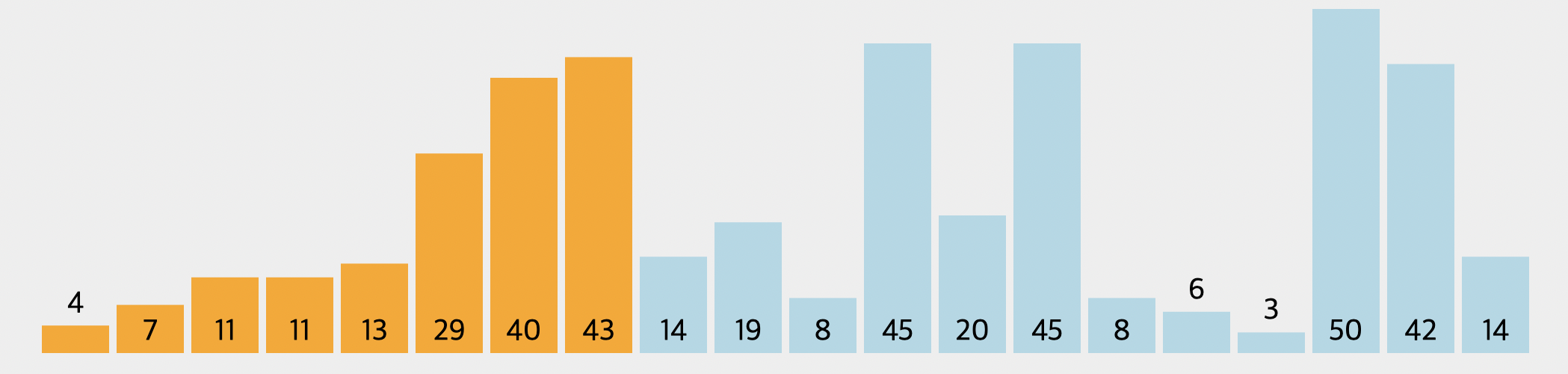
그리고 7보다 큰 숫자들이 모두 오른쪽으로 이동하게 되고 결국 7보다 작은 4를 만나게 됩니다. 4를 만나게 되면 여기서 숫자 7은 멈추고 그 다음 자리를 찾아서 들어가게 되는 것입니다.
이렇게 본인의 자리를 찾아서 들어간다라는 의미에서 삽입 정렬이라고 생각하시면 되겠습니다. 그렇다면 삽입 정렬의 원리는 이해하셨을 거라 생각하고 코드로 구현하는 법에 대해 알아보겠습니다.
insertionSort
function insertionSort(arr) {
for (let i = 1; i < arr.length; i++) {
let currentNum = arr[i];
j = i - 1;
while (j >= 0 && arr[j] > currentNum) {
arr[j + 1] = arr[j];
arr[j] = currentNum;
currentNum = arr[j];
j--;
}
}
return arr;
}삽입 정렬은 위와 같이 코드로 나타낼 수 있습니다. 개인적으로 저의 경우에는 삽입 정렬이 가장 구현하기 어려워서 직접 못하고 완료된 코드를 보고도 한 번에 이해하지 못했습니다.
알고리즘이 익숙하지 않은 분들은 어려운 것이 당연하니 좌절하지 마시고 단계별로 노트에 직접 써보시면서 공부하시는 것을 추천드립니다. 일단, 선택 정렬과 비슷한 방법으로 직접 예시를 통해 살펴보겠습니다.
[34, 22, 10, 19, 27]
| i | j | j + 1 | currentNum |
|---|---|---|---|
| 1 | 0 | 1 | arr[i] = 22 |
| 2 | 1 | 2 | arr[i] = 10 |
| 2 | 0 | 1 | arr[j] = 10 |
선택 정렬에서는 최소값이 중요한 개념이었다면, 삽입 정렬에서는 현재값이 중요합니다. 0번째는 이미 정렬이 완료된 것으로 볼 수 있기 때문에 i가 1부터 시작할 수 있습니다. 그리고 이 값을 현재값이라는 변수에 저장합니다.
이후 새로운 변수 j가 등장합니다. j는 반복문이 진행되면서 앞으로 이동하게 되는 변수입니다. i가 1일 때는 0번째와 비교하고, i가 2일 때는 1번째와 비교하는 방식으로 진행되므로 j = i - 1이 됩니다.
while (j >= 0 && arr[j] > currentNum) {
}본격적으로 반복문에 대해 알아봅시다. 조건은 j가 0 이상인 경우에만 반복이 진행됩니다. 이는 쉽게 이해하실 수 있을 거라 생각합니다. 그리고 arr[j] > currentNum은 바로 불필요한 반복을 줄이는 것입니다.
[22, 34]
예를 들어, 위와 같은 경우라면 반복은 진행되지 않아도 됩니다. currentNum은 arr[i]이기 때문에 34가 되고, 34는 22보다 크기 때문에 반복문이 진행되지 않습니다. 반대의 경우에만 반복문이 진행되면 되기 때문에 arr[j] > currentNum이 되는 것입니다. 쉽게 말해, 앞의 숫자가 뒤의 숫자보다 큰 경우만 반복이 진행된다고 보시면 됩니다.
while (j >= 0 && arr[j] > currentNum) {
arr[j + 1] = arr[j];
arr[j] = currentNum;
currentNum = arr[j];
j--;
}그렇다면 반복문의 조건을 알아보았으니 안의 내용을 살펴봅시다.
[34, 22, 10]
| i | j | j + 1 | currentNum |
|---|---|---|---|
| 1 | 0 | 1 | arr[i] = 22 |
| 2 | 1 | 2 | arr[i] = 10 |
| 2 | 0 | 1 | arr[j] = 10 |
먼저, 첫 번째의 i가 1인 경우, 정렬을 하는 22가 앞의 숫자보다 작기 때문에 앞으로 이동을 해주어야합니다. 이를 위한 첫 단계는 arr[j+1] = arr[j]입니다. 22를 34로 먼저 바꿔주는 것입니다. 이를 통해, 배열은 [34, 34, 10]이 되었습니다.
이제 앞의 34를 currentNum인 22로 바꿔주면 되겠죠? 이렇게 arr[j] = currentNum이 되는 것입니다. [22, 34, 10]이 됩니다.
하지만 여기서 끝이 나면 안됩니다. 배열만 바꿔주는 것이 아니라 currentNum에 저장된 변수 또한 바꿔주어야 이후의 과정에서도 정렬이 진행되므로 currentNum = arr[j] 코드를 작성해줍니다. 마지막으로는 j--를 통해 비교하는 화살표를 왼쪽으로 이동시켜주어야 합니다.
아래에 i가 2인 경우에도 표를 통해 표시해두었으니 직접 손으로 써보시며 이후의 과정을 알아보시면 더욱 쉽게 이해가 되니 꼭 추천 드립니다.
그러면 이제 마지막으로 저번 시간에 배운 버블 정렬과 함께 Big O Notation에 대해 알아봅시다.
3. Big O Notation
그렇다면 버블, 선택, 삽입 정렬 총 3가지의 Big O Notation에 대해 알아봅시다.
| 종류 | (BEST) 시간 복잡도 | (Average) 시간 복잡도 | (WORST) 시간 복잡도 | 공간 복잡도 |
|---|---|---|---|---|
| Bubble | O(n) | O(n²) | O(n²) | O(1) |
| Insertion | O(n) | O(n²) | O(n²) | O(1) |
| Selection | O(n²) | O(n²) | O(n²) | O(1) |
이처럼 버블 정렬과 삽입 정렬은 이미 정렬이 된 상태라면 O(n)이 됩니다. 그러나 선택 정렬은 모든 배열의 데이터를 탐색하여 최소값을 찾아내야 하므로 정렬이 된 상태라 하더라도 시간 복잡도가 O(n²)이 되는 점이 차이라고 할 수 있습니다.
물론, 시간 복잡도는 평균값이 중요하기 때문에 세 정렬 방법 모두 O(n²)이라는 점을 명심해야 합니다. 이렇게 이번까지 알아본 세 종류의 정렬은 시간 복잡도가 O(n²)이므로 자주 사용되는 정렬 방법은 아닙니다.
실제로는 이후부터 알아볼 정렬 방법이 자주 사용되지만, 위 3가지의 정렬 방법을 잘 모르신다면 이해가 어려울 수 있으니 기본적인 이 정렬들에 대해서는 개념에 대해 익숙해지셔야 합니다😉
