Merge Sort

이전 시간까지 배운 기본적인 정렬에 이어 이번부터는 다소 어렵지만, 매우 획기적인 정렬 방법에 대해 배워보도록 하겠습니다.

Merge Sort는 간단히 말해 병합 정렬로 배열을 잘개 쪼개어 정렬을 한 뒤, 이후 병합을 하는 방식으로 진행이 됩니다. 이번에도 visualgo 사이트로 직접 들어가서 보시면 이해에 큰 도움이 됩니다.

추가적으로 JavaScript 코드는 아니지만, 유튜버 코딩하는거니님의 병합 정렬 설명을 영상으로 확인해보시면, 더욱 쉽게 이해하실 수 있습니다.

1. Merge Sort

---

병합 정렬은 위에서 언급했다시피 잘개 쪼개서 병합하는 정렬입니다. 다시 말해, 모든 숫자를 다 나눈 다음에 병합하는 방식으로 정렬을 진행합니다.

병합 정렬은 단순하지 않은 정렬 시리즈 중 제일 단순한 분할 정복 알고리즘입니다.

[8, 3, 5, 4, 7, 6, 1, 2]

이번에도 예를 들어서 살펴보도록 하겠습니다. 위의 배열을 병합 정렬을 통해 정렬을 진행한다고 가정해봅시다. 먼저 잘개 쪼개는 과정이 필요합니다.

[8, 3, 5, 4, 7, 6, 1, 2] //split
[8, 3, 5, 4][7, 6, 1, 2] //split
[8, 3][5, 4][7, 6][1, 2] //split
[8][3][5][4][7][6][1][2] //split

이처럼 총 3단계를 통해 배열을 쪼갰습니다. 마지막의 배열을 보시면, 배열의 데이터가 1개씩 남아있는 것을 확인해보실 수 있습니다. 이렇게 배열은 데이터 1개 이하로 남을 때까지 분할을 반복해줘야 합니다.

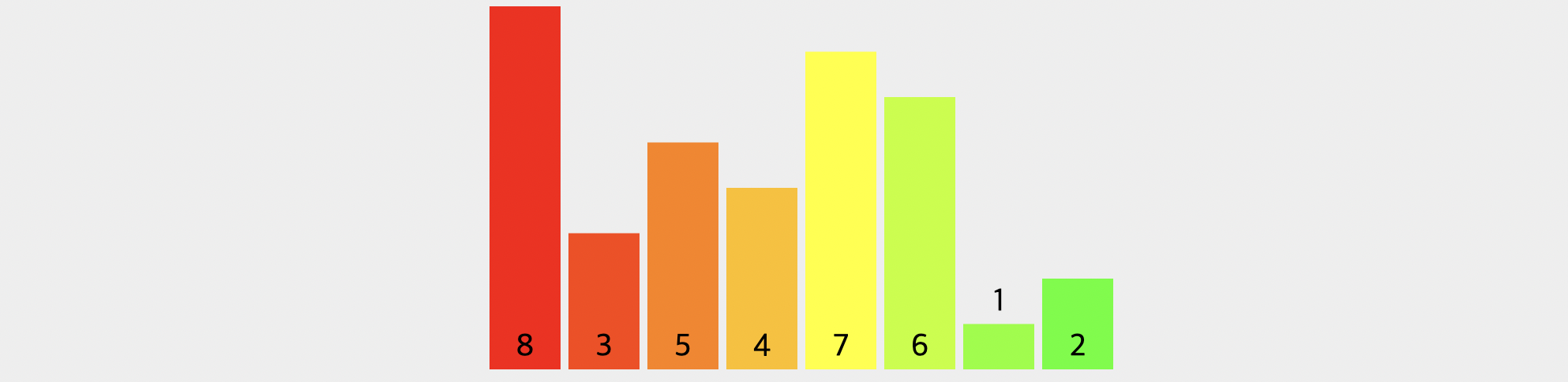
위의 그림에서 보시다시피 총 8개의 배열 데이터가 모두 색깔이 다른 것을 확인하실 수 있고, 이는 분할이 완료된 상태라는 것을 의미합니다. 그렇다면, 이제 본격적으로 병합을 진행합니다.

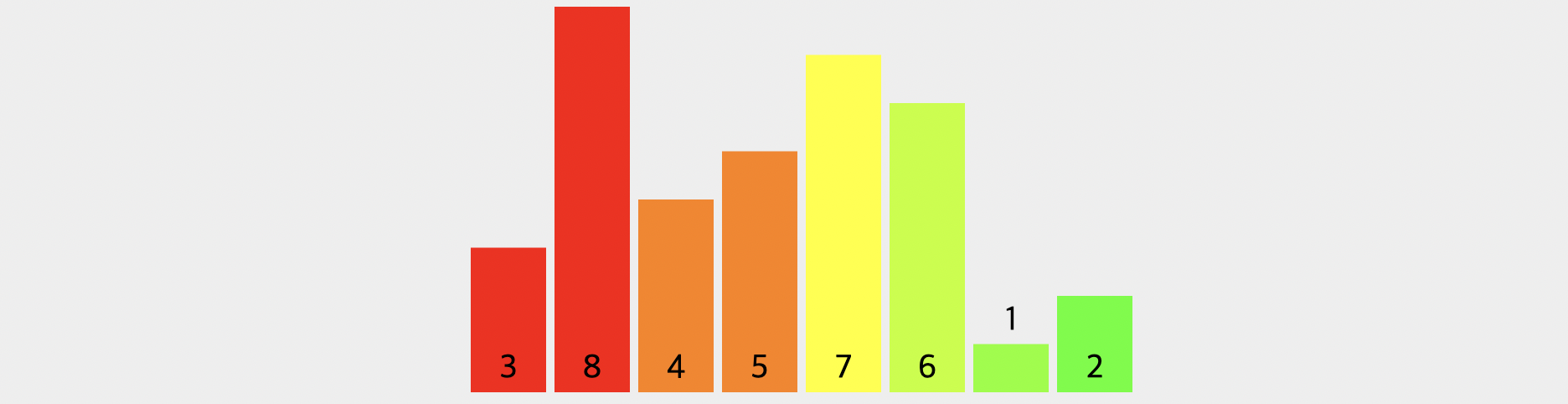
[8][3][5][4][7][6][1][2] //split
[3, 8][5, 4][7, 6][1, 2] //merge
[3, 8][4, 5][7, 6][1, 2] //merge

먼저, 가장 앞에서부터 병합을 시작합니다. 8과 3을 비교하게 되고 앞의 숫자가 크다면 두 개의 자리를 바꿔주고 병합을 합니다. 그리고 난 뒤, 5와 4를 비교하고 위와 똑같이 분할과 정복을 진행합니다. 이를 통해, 두 번의 병합을 진행했습니다.

이후에는 어떠한 방식으로 진행될까요?

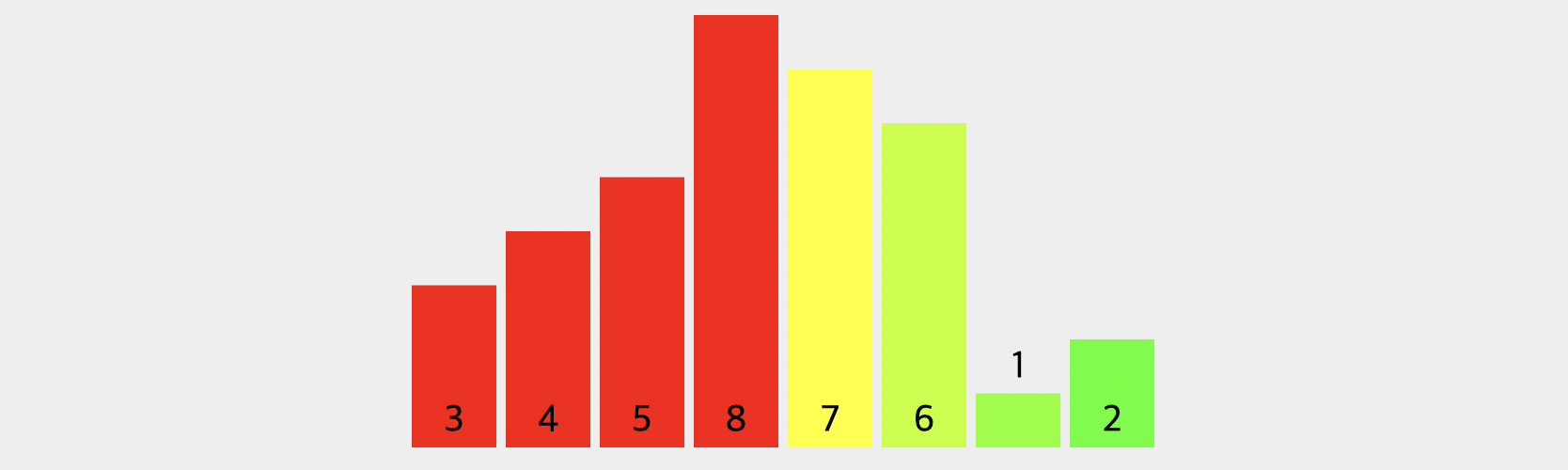
[3, 8][4, 5][7, 6][1, 2] //merge
[3, 4, 5, 8][7, 6][1, 2] //merge

예상하신 것처럼 앞의 4개를 분할, 정복하여 병합 정렬이 진행됩니다. 현재 빨간색으로 표시된 앞의 4개 부분은 정렬이 모두 완료된 상태입니다. 이후에는 오른쪽 4개 부분이 위와 같은 방식으로 정렬이 됩니다.

병합 정렬의 기본적인 개념은 크게 어렵지 않기 때문에 이해하셨으리라 생각합니다. 그렇다면 이를 코드로 구현해보도록 합시다.

다만, 병합 정렬은 Divide & Conquer 즉, 분할 정복 방식으로 진행되는 코드입니다. 이를 코드로 나타내기 위해 정복 과정인 병합을 먼저 코드로 작성한 후, 분할 정복을 함께 재귀 함수 방식으로 구현해야 합니다.

merge([1, 10, 50], [2, 14, 99, 100])

위의 배열을 병합하는 과정을 코드로 작성해봅시다.

1.1 merge

---

function merge(arr1, arr2) {
  let results = [];
  let i = 0;
  let j = 0;
  
  while (i < arr1.length && j < arr2.length) {
    if (arr1[i] > arr2[j]) {
      results.push(arr1[i]);
      i++;
    } else {
      results.push(arr2[j]);
      j++;
    }
  }
  
  while (i < arr1.length) {
    results.push(arr1[i]);
    i++;
  }
  while (j < arr2.length) {
    results.push(arr2[j]);
    j++;
  }
}

병합 로직은 위와 같이 작성할 수 있습니다. 긴 코드로 복잡해보이지만, 실제로는 전혀 그렇지 않습니다. 먼저, results라는 변수에 병합한 뒤 새로운 배열을 반환하여 저장하도록 합니다.

그리고 i와 j는 배열 데이터를 서로 비교하여 오름차순으로 정렬을 진행하는 화살표입니다.

while (i < arr1.length && j < arr2.length) {
  if (arr1[i] < arr2[j]) {
    results.push(arr1[i]);
    i++;
  } else {
    results.push(arr2[j]);
    j++;
  }
}

먼저, 위와 같이 나타낸 코드를 살펴봅시다.

조건은 i와 j가 각각 배열의 길이가 되기 전까지 반복하게 합니다. 그리고 if 조건문을 사용하여 두 수를 비교하여 작은 숫자를 앞으로 정렬합니다. 그리고 화살표(i, j)를 오른쪽으로 이동시켜줄 수 있도록 1씩 증가시키면 됩니다.

그렇다면, 위에서 말한 예시를 현재의 코드로 실행하면 어떠한 배열이 완성되는지 확인해봅시다.

merge([1, 10, 50], [2, 14, 99, 100])
i = 3, j = 2, results = [1, 2, 10, 14, 50]

while 반복문을 끝까지 실행했지만, results 변수에 담긴 배열은 8개의 배열 데이터가 아닌 5개만 담겨있습니다. 그 이유는 i가 arr1.length인 3까지 도착하여 반복문이 끝났기 때문입니다. 그렇다면, arr2의 나머지를 넣어주면 됩니다.

while (i < arr1.length) {
  results.push(arr1[i]);
  i++;
}
while (j < arr2.length) {
  results.push(arr2[j]);
  j++;
}

그 코드가 바로 위의 코드입니다. 위의 예시는 while (i < arr1.length)를 넘어 while (j < arr2.length) 반복문이 실행되겠죠. 반대의 경우에는 앞의 코드가 실행되며 병합이 끝까지 완료될 수 있도록 합니다.

merge([1, 10, 50], [2, 14, 99, 100])
i = 3, j = 4, results = [1, 2, 10, 14, 50, 99, 100]

위와 같이 병합이 완벽하게 끝났습니다. 그렇다면 이제 Divide & Conquer에서 정복 과정이 끝났으므로 분할 과정을 추가해주면 됩니다. 이를 코드로 구현해봅시다.

1.2 mergeSort

function mergeSort(arr) {
  if (arr.length <= 1) return arr;
  
  let mid = Math.floor(arr.length / 2);
  let left = mergeSort(arr.slice(0, mid));
  let right = mergeSort(arr.slice(mid));
  return merge(left, right);
}

위와 같이 코드를 작성하여 배열을 length가 1 이하가 될 수 있도록 잘게 쪼개줍니다. 여기서 if (arr.length <= 1) return arr; 코드는 base case로서 재귀 함수의 종료 조건을 명시해줄 수 있도록 합니다.

let mid = Math.floor(arr.length / 2);
let left = mergeSort(arr.slice(0, mid));
let right = mergeSort(arr.slice(mid));

이후 배열을 recursive case로 재귀적으로 계속해서 호출할 함수를 작성해줍니다. 배열을 반으로 나누어주어야하기 때문에 mid 변수에 배열 길이의 반을 할당합니다.

그리고 이 mid 변수를 활용하여 배열을 나누는 slice 메소드를 활용해줍니다. 왼쪽과 오른쪽을 base case인 배열의 길이가 1까지 나눠주고 이후 return merge(left, right)를 통해 배열을 병합해주면 끝이 납니다.

저에게도 아직 익숙치 않은 재귀 함수이기 때문에 로직은 머리 속에서 어느 정도가 되었지만, 실제로 직접 코드를 작성하라고 하면 어려움을 겪습니다. 병합 정렬과 같은 재귀 함수는 여러 번 코드를 직접 작성하며 공부해야할 것 같습니다.

1.3 Big O Notation

종류	(BEST) 시간 복잡도	(Average) 시간 복잡도	(WORST) 시간 복잡도	공간 복잡도
Merge	O(n log n)	O(n log n)	O(n log n)	O(n)

병합 정렬의 시간 복잡도는 위와 같이 계산할 수 있습니다. n log n의 개념이 생소하실 것이라 생각합니다. 이를 예를 들어서 살펴보도록 하겠습니다.

[8, 3, 5, 4, 7, 6, 1, 2] //split
[8, 3, 5, 4][7, 6, 1, 2] //split 1
[8, 3][5, 4][7, 6][1, 2] //split 2
[8][3][5][4][7][6][1][2] //split 3

위처럼 8개의 길이를 가진 배열을 나누는 단계가 총 3단계로 이루어져 있습니다. 이렇게 분할의 과정이 log n이라고 볼 수 있습니다. 배열이 16개라면 4단계, 그리고 32개라면 5단계를 통해 길이가 1 이하인 배열로 나눌 수 있습니다.

정확히 따지자면, log₂n이라고 할 수 있으나 여기서는 2를 생략해주게 됩니다. 그리고 여기에 n을 곱해주는 것은 분할 다음의 정복, 병합의 과정입니다.

1개의 배열에서 2개로, 2개의 배열에서 4개 그리고 마지막으로 길이가 8일 배열로 병합하는 과정은 n의 단계가 필요합니다. 이를 모두 계산하여 병합 정렬의 시간 복잡도는 O(n log n)으로 계산이 됩니다.

여기서 중요한 것은 이전에 배웠던 버블, 삽입, 선택 정렬의 시간 복잡도인 O(n²)과 현저하게 차이가 나는 시간 단축을 보여준다는 것입니다.

코드가 복잡한만큼 더 빠른 구현 속도를 보여주므로 잘 학습할 수 있도록 해야겠습니다🧐