LoRA(Low Rank Adaptation)

LoRA(Low-Rank Adaptation)는 대규모 언어 모델(LLM)을 효율적으로 미세 조정하는 기술입니다. 이 방법의 핵심 아이디어는 모델의 가중치를 직접 업데이트하는 대신, 낮은 순위(low-rank) 행렬을 사용하여 모델을 조정하는 것입니다. 이를 통해 적은 수의 학습 가능한 매개변수로도 효과적인 모델 조정이 가능해집니다.

LoRA의 작동 원리를 간단한 예시로 설명해보겠습니다:

1. 기본 모델:
   예를 들어, GPT-3와 같은 대규모 언어 모델이 있다고 가정해봅시다. 이 모델은 수십억 개의 매개변수를 가지고 있습니다.

2. 특정 작업:
   이 모델을 의료 분야의 질문에 답변하도록 특화시키고 싶다고 가정해봅시다.

3. 전통적인 미세 조정:
   일반적인 방법으로는 전체 모델의 매개변수를 업데이트해야 합니다. 이는 많은 계산 자원과 시간이 필요합니다.

4. LoRA 적용:

   • 원본 가중치 행렬 W를 그대로 유지합니다.
   • 두 개의 작은 행렬 A와 B를 도입합니다. A는 d x r 크기, B는 r x k 크기입니다. 여기서 r은 낮은 순위를 나타냅니다.
   • 새로운 가중치는 W + AB로 표현됩니다.

5. 학습 과정:

   • 원본 모델 W는 고정된 상태로 유지됩니다.
   • A와 B만 학습됩니다. 이는 전체 매개변수의 아주 작은 부분입니다.

6. 결과:

   • 의료 관련 질문에 대해 더 정확하고 전문적인 답변을 제공할 수 있게 됩니다.
   • 원본 모델의 일반적인 능력은 유지됩니다.

7. 장점:

   • 메모리 효율성: AB는 W보다 훨씬 작습니다.
   • 계산 효율성: 적은 수의 매개변수만 업데이트하면 됩니다.
   • 유연성: 다른 작업을 위해 다른 LoRA 모듈을 쉽게 교체할 수 있습니다.

LoRA를 사용하면, 예를 들어 100GB 크기의 모델을 몇 MB의 추가 매개변수만으로 특정 작업에 맞게 조정할 수 있습니다. 이는 특히 제한된 리소스 환경에서 LLM을 다양한 작업에 적용할 때 매우 유용합니다.

---

예시

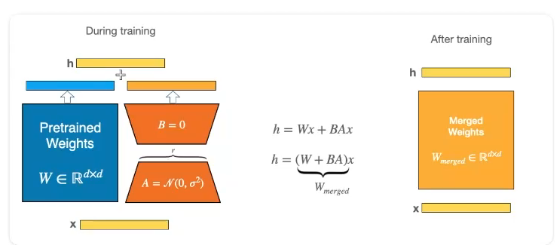
LoRA의 A와 B 행렬 상세 설명

   ### 행렬 크기와 매개변수 수

   원본 가중치 행렬 W의 크기를 d x k라고 가정해봅시다.
   - A 행렬: d x r
   - B 행렬: r x k
   
   여기서 r은 순위(rank)로, 일반적으로 매우 작은 값입니다(예: 8, 16, 32 등).

   매개변수 수 비교:
   - W의 매개변수 수: d * k
   - A와 B의 총 매개변수 수: d * r + r * k = r * (d + k)

   예시:
   d = 1000, k = 1000, r = 16인 경우
   - W의 매개변수 수: 1000 * 1000 = 1,000,000
   - A와 B의 총 매개변수 수: 16 * (1000 + 1000) = 32,000

   이 경우, LoRA는 원본 매개변수의 약 3.2%만 사용합니다.

   ### 학습 과정

   1. 초기화: A와 B는 작은 무작위 값으로 초기화됩니다.

   2. 순전파(Forward Pass):
      - 입력 x에 대해 y = W*x + (A*B)*x 계산
      - W는 고정되어 있으므로 계산되지 않음

   3. 역전파(Backward Pass):
      - 손실 함수의 그래디언트가 A와 B로만 전파됨
      - ∂L/∂A와 ∂L/∂B 계산 (L은 손실 함수)

   4. 매개변수 업데이트:
      - A = A - η * ∂L/∂A
      - B = B - η * ∂L/∂B
      (η는 학습률)

   5. 반복: 2-4 단계를 여러 번 반복

   ### 메모리 및 계산 효율성

   - 메모리 효율: A와 B는 W보다 훨씬 작아 저장 공간이 적게 필요
   - 계산 효율: 역전파 시 적은 수의 매개변수만 업데이트
   - 유연성: 다른 작업을 위해 A와 B만 교체하면 됨

   ### 실제 적용 예시

   GPT-3 (175B 매개변수) 모델에 LoRA 적용 시:
   - r = 4일 때, 추가되는 매개변수는 약 350만 개
   - 이는 원본 모델의 0.002%에 불과
   - 특정 작업에서 전체 미세 조정과 비슷한 성능 달성 가능

---

LoRA는 일반적으로 모델의 여러 레이어에 적용됩니다.

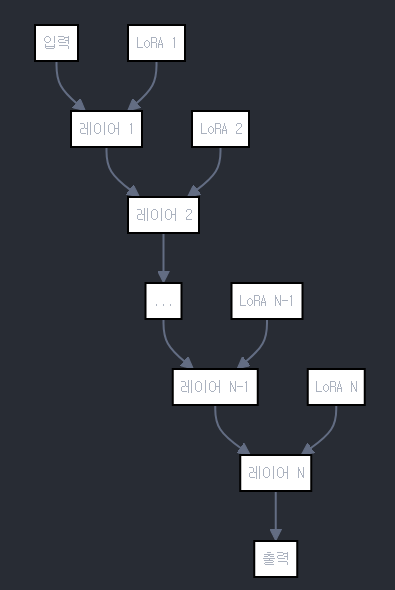
LoRA를 여러 레이어에 적용하는 방식에 대해 자세히 설명드리겠습니다:

1. 다중 레이어 적용:

   • LoRA는 일반적으로 모델의 여러 레이어에 적용됩니다.
   • 각 레이어마다 독립적인 LoRA 모듈이 붙습니다.

2. 적용 위치:

   • 주로 트랜스포머 모델의 어텐션 레이어에 적용됩니다.
   • 구체적으로는 각 레이어의 Query, Key, Value 가중치 행렬과 출력 투영 행렬에 적용될 수 있습니다.

3. 독립적인 파라미터:

   • 각 레이어의 LoRA 모듈은 독립적인 파라미터 세트(A와 B 행렬)를 가집니다.
   • 이는 각 레이어가 서로 다른 방식으로 조정될 수 있음을 의미합니다.

4. 선택적 적용:

   • 모든 레이어에 LoRA를 적용할 필요는 없습니다.
   • 일부 구현에서는 특정 간격으로 레이어를 선택하거나, 상위 또는 하위 몇 개의 레이어에만 적용하기도 합니다.

5. 랭크 설정:

   • 각 LoRA 모듈의 랭크(저차원 행렬의 차원)를 다르게 설정할 수 있습니다.
   • 이를 통해 각 레이어의 조정 정도를 세밀하게 제어할 수 있습니다.

6. 계산 효율성:

   • 여러 레이어에 적용되더라도, 각 LoRA 모듈의 파라미터 수가 적기 때문에 전체적인 효율성은 유지됩니다.

7. 유연한 구성:

   • 어떤 레이어에 LoRA를 적용할지, 각 LoRA 모듈의 랭크를 어떻게 설정할지 등을 실험을 통해 최적화할 수 있습니다.

8. 통합 과정:

   • 학습 후, 각 레이어의 LoRA 가중치는 해당 레이어의 원본 가중치에 더해져 통합될 수 있습니다.
   • 이를 통해 추론 시 추가적인 계산 오버헤드를 최소화할 수 있습니다.

이러한 방식으로 LoRA를 여러 레이어에 적용함으로써, 모델의 다양한 수준의 특징을 효과적으로 조정할 수 있습니다. 이는 모델이 특정 태스크나 도메인에 더 잘 적응할 수 있게 해주면서도, 전체 모델을 파인튜닝하는 것보다 훨씬 적은 파라미터만으로 효과적인 적응이 가능하게 합니다.

전체구조1

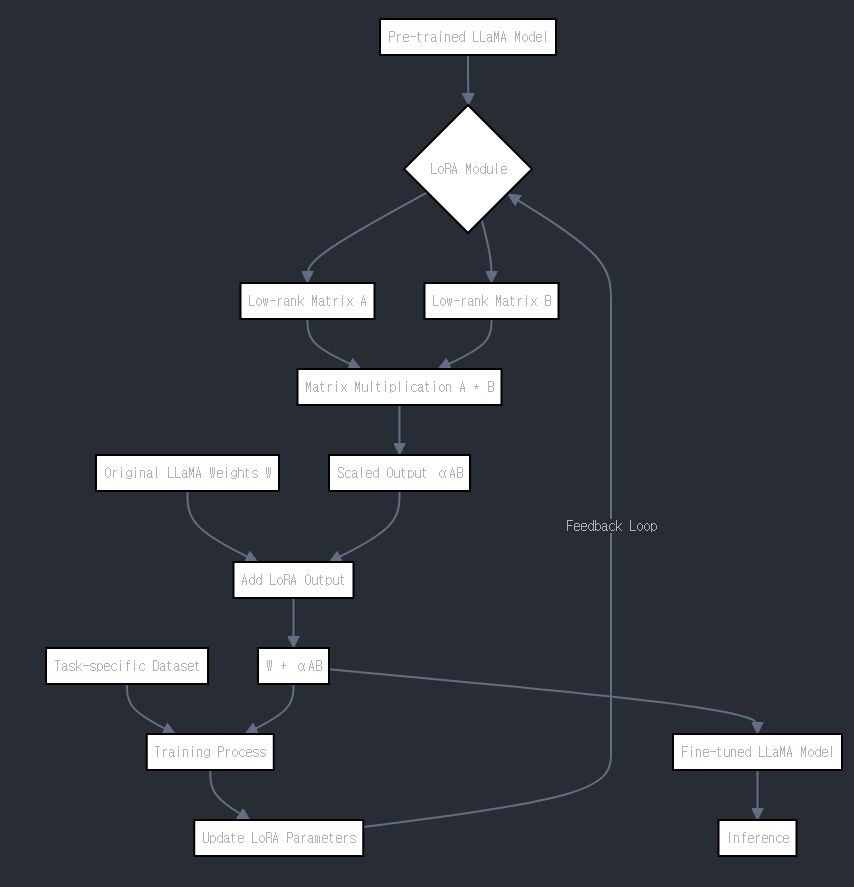
전체구조2

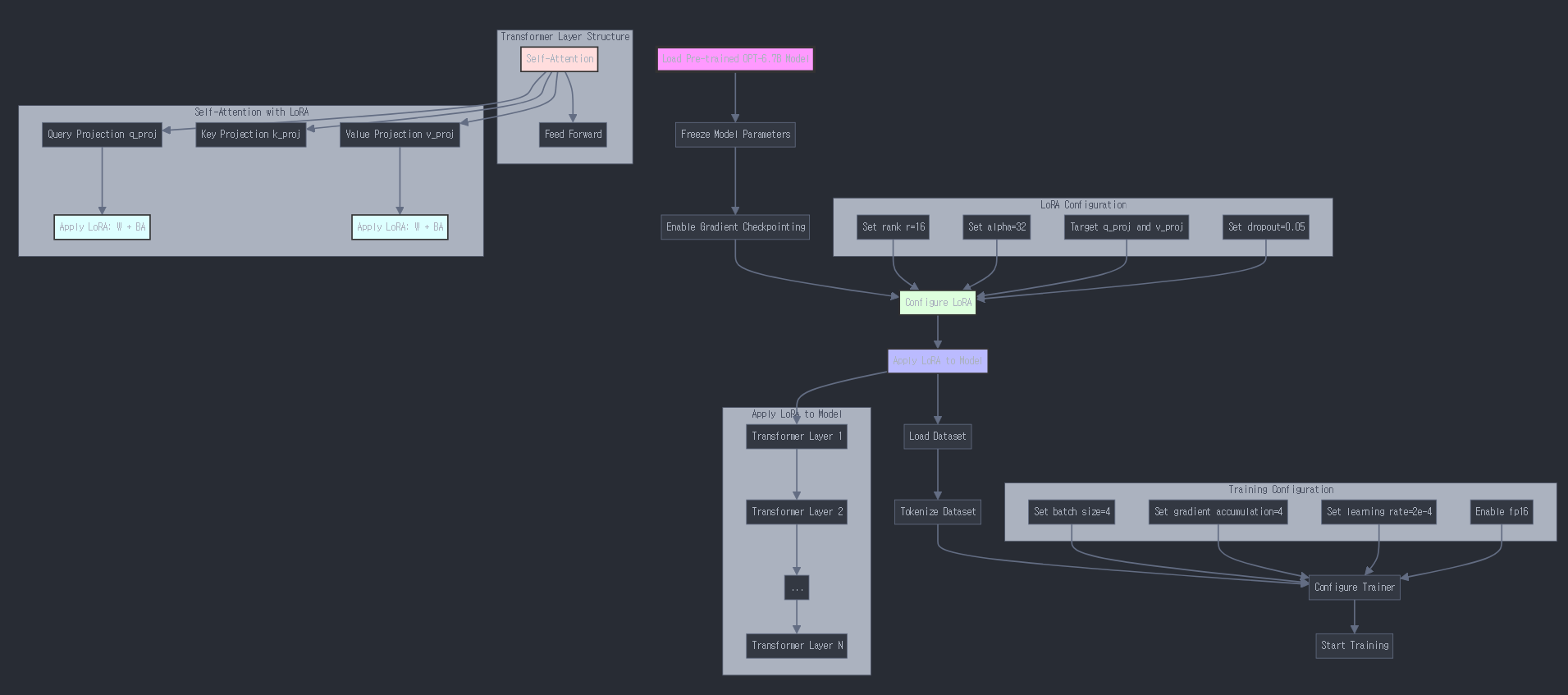
• LoRA는 Transformer모델의 Q,K,V전부 적용될 수 있으며 일부에 적용할 수도 있다.
  • 성능을 실험하며 최적을 구해야한다.

---

r값과 alpha값

1. LoRA의 기본 구조:

# 기존 가중치 행렬 W의 업데이트
# W = W₀ + BA
# 여기서 B는 (d × r) 행렬, A는 (r × k) 행렬

class LoRALayer:
    def __init__(self, base_layer, rank=8, alpha=16):
        self.base_layer = base_layer  # 원본 가중치 W₀
        self.rank = rank             # r값
        self.alpha = alpha           # 스케일링 파라미터
        
        # LoRA 가중치 초기화
        self.lora_A = nn.Parameter(torch.zeros(rank, base_layer.weight.size(1)))
        self.lora_B = nn.Parameter(torch.zeros(base_layer.weight.size(0), rank))
        
    def forward(self, x):
        # 기본 변환
        base_output = self.base_layer(x)
        
        # LoRA 변환
        lora_output = (self.lora_B @ self.lora_A) * (self.alpha / self.rank)
        
        # 결합
        return base_output + lora_output

2. alpha의 역할:

# alpha는 LoRA 업데이트의 크기를 조절
final_weight = base_weight + (alpha/r) * (B @ A)

# 예시 1: 작은 alpha
config_small = LoraConfig(
    r=8,
    alpha=8,  # alpha/r = 1
    target_modules=['q_proj', 'v_proj']
)
# 결과: 더 보수적인 업데이트

# 예시 2: 큰 alpha
config_large = LoraConfig(
    r=8,
    alpha=32,  # alpha/r = 4
    target_modules=['q_proj', 'v_proj']
)
# 결과: 더 공격적인 업데이트

3. 실제 구현에서의 alpha:

# 실제 PyTorch 구현 예시
class LoRALinear(nn.Module):
    def __init__(self, 
                 base_layer,
                 rank=8, 
                 alpha=16):
        super().__init__()
        
        self.base_layer = base_layer
        self.rank = rank
        self.scaling = alpha / rank
        
        # 입력 차원
        in_features = base_layer.in_features
        # 출력 차원
        out_features = base_layer.out_features
        
        # LoRA 행렬 초기화
        self.lora_down = nn.Linear(in_features, rank, bias=False)
        self.lora_up = nn.Linear(rank, out_features, bias=False)
        
        # 가중치 초기화
        nn.init.kaiming_uniform_(self.lora_down.weight, a=math.sqrt(5))
        nn.init.zeros_(self.lora_up.weight)
        
    def forward(self, x):
        # 기본 변환
        base_output = self.base_layer(x)
        
        # LoRA 변환 (스케일링 포함)
        lora_output = self.lora_up(self.lora_down(x)) * self.scaling
        
        return base_output + lora_output

4. alpha 선택 가이드:

# 1. 안정적인 학습 (alpha = r)
config_stable = LoraConfig(
    r=8,
    alpha=8,  # alpha/r = 1
    target_modules=['q_proj', 'v_proj']
)
# 특징: 
# - 안정적인 학습
# - 더 작은 업데이트 스텝

# 2. 일반적인 설정 (alpha = 2r)
config_normal = LoraConfig(
    r=8,
    alpha=16,  # alpha/r = 2
    target_modules=['q_proj', 'v_proj']
)
# 특징:
# - 균형잡힌 학습
# - 적당한 업데이트 크기

# 3. 공격적인 학습 (alpha = 4r)
config_aggressive = LoraConfig(
    r=8,
    alpha=32,  # alpha/r = 4
    target_modules=['q_proj', 'v_proj']
)
# 특징:
# - 빠른 적응
# - 더 큰 업데이트 스텝

5. alpha의 영향:

• 학습 속도:

  • 큰 alpha → 빠른 학습, 불안정할 수 있음
  • 작은 alpha → 안정적 학습, 더 오래 걸림

• 메모리 사용:

  • alpha는 메모리 사용량에 영향을 주지 않음
  • 단순히 스케일링 파라미터로 작용

• 최종 성능:

  • 적절한 alpha는 더 좋은 성능으로 수렴
  • 너무 큰 alpha는 오버슈팅 위험

6. 권장 설정:

• 일반적인 경우: alpha = 2r
• 안정성 중시: alpha = r
• 빠른 적응 필요: alpha = 4r

이러한 구조에서 alpha는 LoRA 업데이트의 강도를 조절하는 핵심 파라미터로, 학습의 안정성과 속도를 결정하는 중요한 역할을 합니다.