마르코프 체인

마르코프 체인은 확률 과정의 일종으로, 다음 상태가 오직 현재 상태에만 의존하는 특성을 가집니다

주요 특징:

• 현재 의존성: 미래 상태는 오직 현재 상태에만 의존하며, 과거 이력은 고려하지 않습니다.
• 전이 확률: 한 상태에서 다른 상태로 변화할 확률을 전이 확률이라 합니다.
• 상태 공간: 시스템이 가질 수 있는 모든 가능한 상태들의 집합입니다.

실제 응용 예시:

• 날씨 예측 모델링
• 주식 시장 분석
• 검색 엔진의 페이지랭크 알고리즘
• 자연어 처리의 텍스트 생성

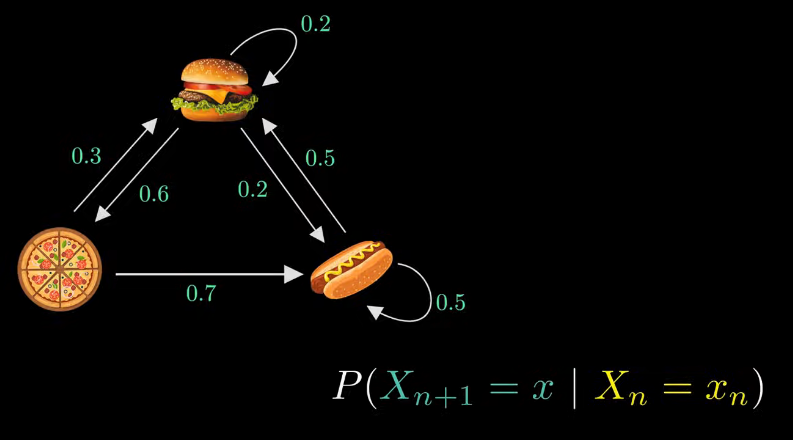
• 각 포인트는 다음날 무엇을 먹을지에 대한 확률이다.
  • ex) 햄버거를 먹고 다음날 피자를 먹을 확률: 0.6
  • ex) 햄버거를 먹고 다시 햄버거를 먹을 확률: 0.2
• 다음 날 무엇을 먹을지 예측할 때 오직 오늘의 상황 만으로 판단한다.
  • (과거에 무엇을 먹었는지는 다음날 무엇을 먹을지 예측할때 생각하지 않는다.)

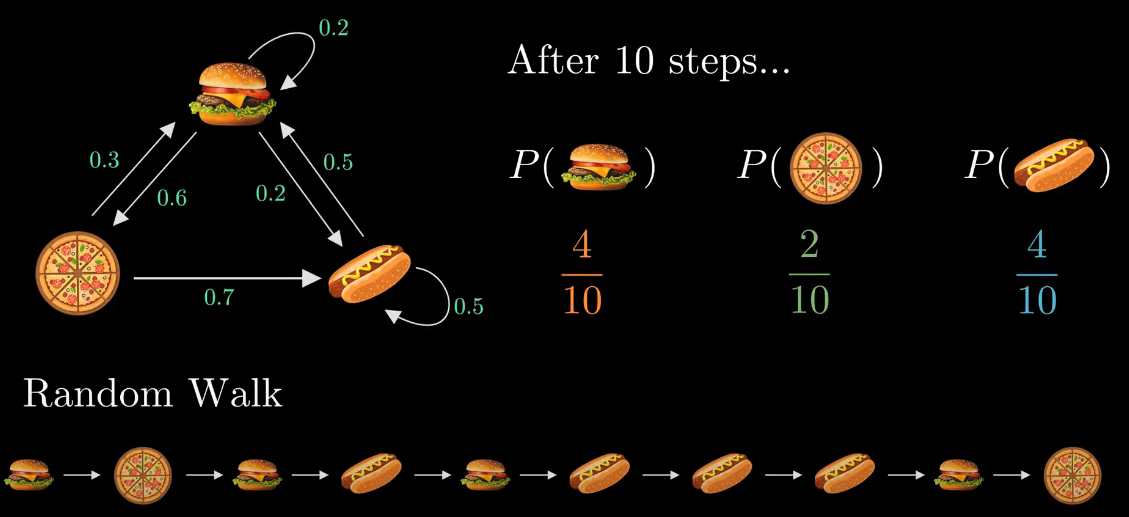
• 햄버거로 시작하여 랜덤 으로 다음에 무엇을 먹을지 10일치를 보자.
  • 햄버거, 피자, 핫도그 확률을 더하면 1이된다.

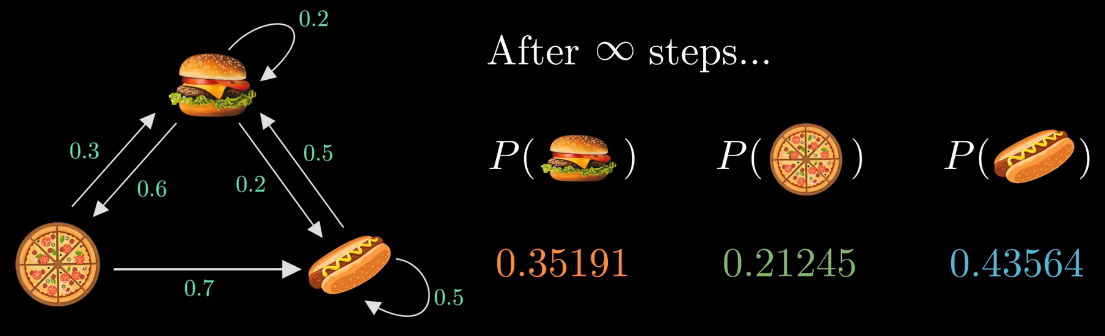
• 이를 무한대로 본다면 위와 같은 확률로 수렴하게 된다.
  • 이를 stationary state라 한다.

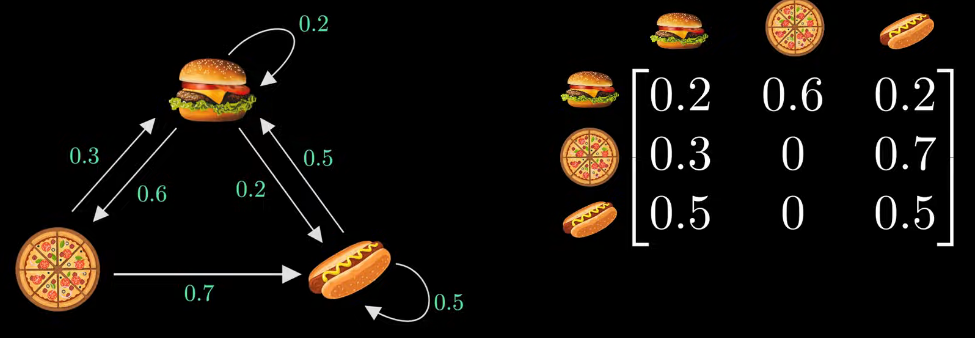
• 이는 인접 행렬로 나타낼 수 있다.

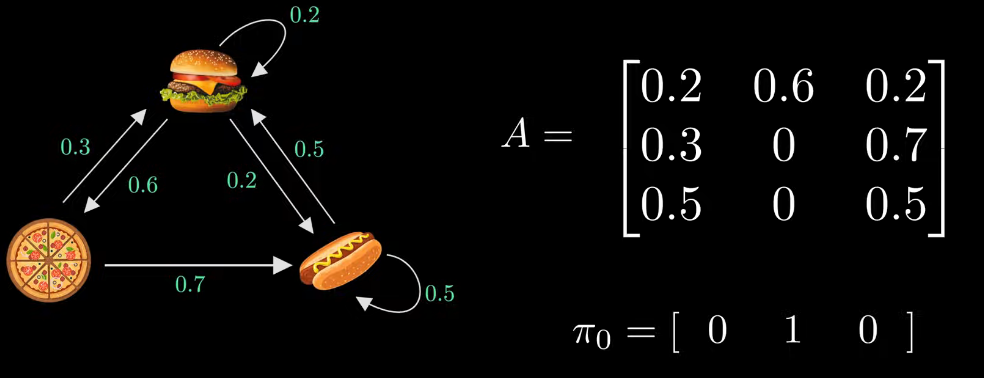
• π0: Random Walk로 첫번째 시작이 피자를 의미한다.

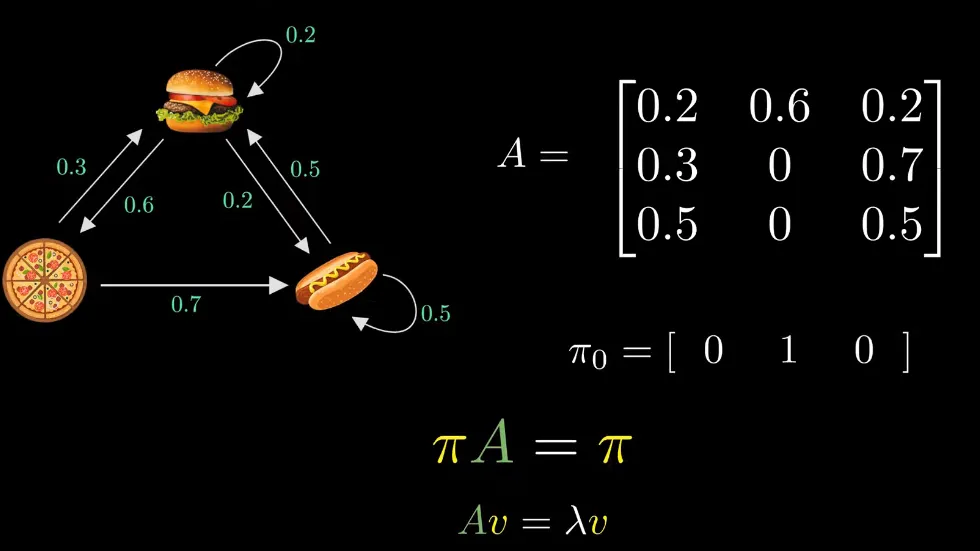
• 위와 같이 계속 계산할 경우 결국 πA = π인 수식이 된다.
  • 즉 π에 A값을 계속 곱해도 결과가 같은 상태이다.
• Av = λv (고유값 방정식): 이 방정식은 정상상태를 찾는 다른 방법
  • A: 전이행렬
  • λ: 고유값
  • v: 고유벡터
  • λ = 1인 고유벡터가 정상상태 확률 분포가 됨

---

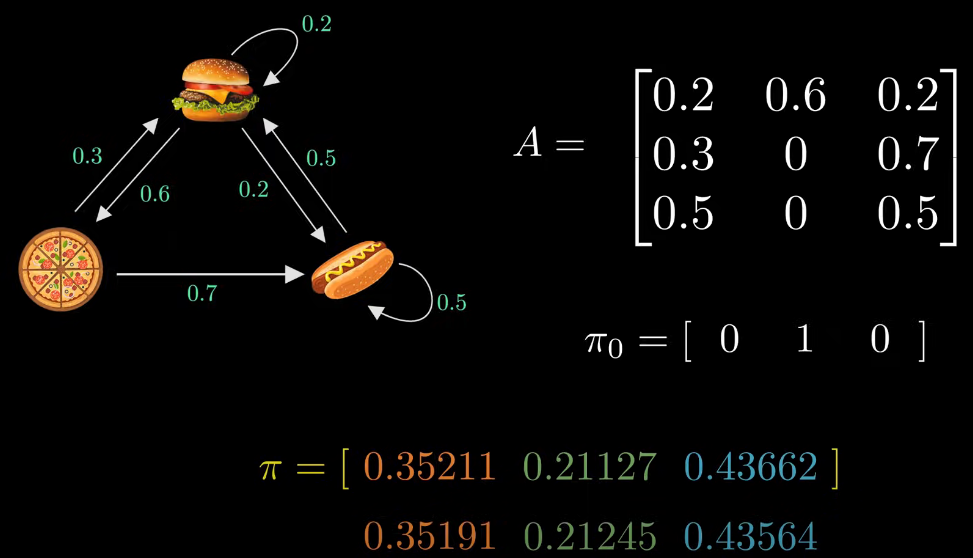
전이행렬 계산

1. 데이터 수집 방법:

• 웹 로그 데이터
• 사용자 행동 추적
• 시스템 로그
• 거래 기록
  등을 통해 상태 전이를 관찰

2. 전이행렬 계산 예시:
   총 1000명의 고객 행동 데이터 수집 결과

상태 B(Browsing)에서의 전이:

• 총 400명이 B상태를 거침
• 200명이 B → B (같은 상태 유지)
• 120명이 B → C (장바구니로 이동)
• 40명이 B → P (바로 구매)
• 40명이 B → E (이탈)

전이확률 계산:
P(B→B) = 200/400 = 0.5
P(B→C) = 120/400 = 0.3
P(B→P) = 40/400 = 0.1
P(B→E) = 40/400 = 0.1

이런 식으로 각 상태에서의 전이를 계산:

상태 C에서의 전이 (300명 관찰):
P(C→B) = 60/300 = 0.2
P(C→C) = 120/300 = 0.4
P(C→P) = 90/300 = 0.3
P(C→E) = 30/300 = 0.1

최종 전이행렬:

      B    C    P    E
B   [0.5  0.3  0.1  0.1]
C   [0.2  0.4  0.3  0.1]
P   [0.3  0.2  0.4  0.1]
E   [0.6  0.2  0.1  0.1]

3. 주의사항:

• 충분한 데이터 수집 필요
• 각 행의 합은 1이 되어야 함
• 시간에 따른 변화 고려
• 이상치 제거 필요
• 데이터의 신뢰성 검증 필요

4. 실제 적용시 고려사항:

• 시간대별 차이
• 요일별 차이
• 계절성
• 특별 이벤트 영향
  등을 고려하여 여러 버전의 전이행렬 구축 가능

---

Stationary 상태와 각 노드의 수 / 전체 수는 어떻게 다른가?

• Stationary의 경우 이전의 상태를 고려하기 때문에 이전 노드가 영향력이 높다면(영향이 높은 상태가 현재 노드를 참조하고 있다면) 점수가 높아진다.
  • ex) 세션으로 부터 클릭을 많이 받은 아이템은 좋은 아이템이다, 이런 영향력 높은 아이템 다음으로 선택이 자주 된 아이템의 경우 클릭이 많지 않아도 좋은 아이템일 수 있다.

ref: https://www.youtube.com/watch?v=i3AkTO9HLXo&list=PLM8wYQRetTxBkdvBtz-gw8b9lcVkdXQKV