페이지랭크는 구글의 공동 창업자인 래리 페이지가 개발한 알고리즘으로, 웹 페이지의 중요도를 평가하는 방법입니다.
핵심 개념:
1. 링크 기반 순위
- 다른 중요한 페이지로부터 링크를 많이 받을수록 해당 페이지의 중요도가 높아집니다
- 단순히 링크의 수가 아닌, 링크를 제공하는 페이지의 중요도도 고려됩니다
-
랜덤 서퍼 모델
- 사용자가 무작위로 웹을 탐색한다고 가정
- 특정 페이지에 도달할 확률이 그 페이지의 중요도를 나타냄
-
수학적 계산
PR(A) = (1-d) + d(PR(T1)/C(T1) + ... + PR(Tn)/C(Tn)) 여기서: - PR(A): 페이지 A의 페이지랭크 값 - d: 감쇠 계수 (보통 0.85) - T1...Tn: A로 링크하는 페이지들 - C(T): 페이지 T에서 나가는 링크 수
특징:
- 반복적 계산을 통해 수렴된 값을 찾음
- 마르코프 체인의 정상 상태 분포를 계산하는 것과 동일
- 웹의 구조를 활용한 객관적 평가 방법
응용 분야:
- 웹 검색 결과 순위 결정
- 소셜 네트워크 분석
- 학술 논문의 영향력 평가
- 추천 시스템
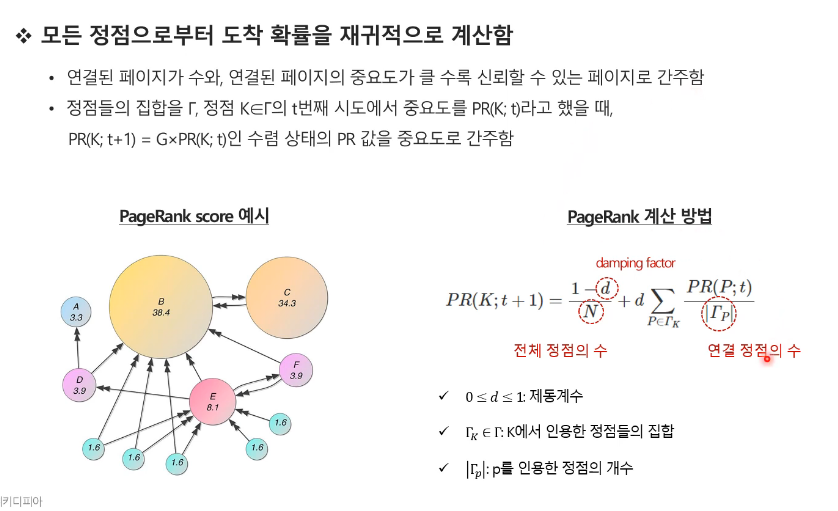
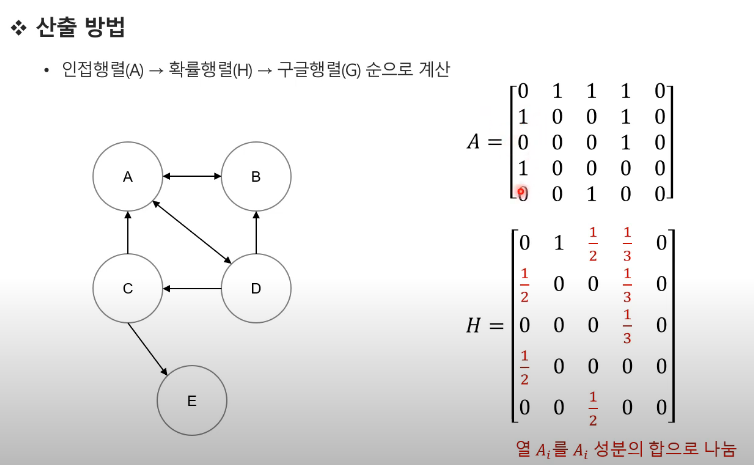
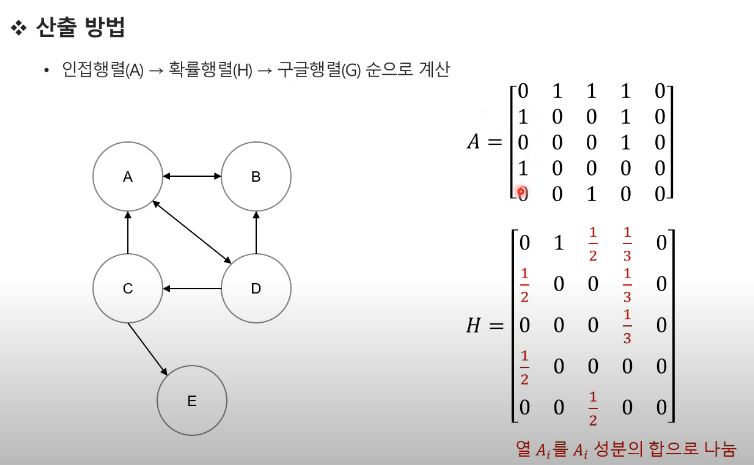
- A는 인접 행렬
- H는 전이 행렬
인접행렬과 전이행렬의 차이.
예를 들어 3개의 페이지(A, B, C)가 있고 다음과 같은 링크가 있다고 해보겠습니다:
A → B
B → C
C → A, B- 인접행렬 (Adjacency Matrix)
- 단순히 링크의 존재(1)와 부재(0)를 나타냅니다.
A B C
A 0 0 1
B 1 0 1
C 0 1 0- 전이행렬 (Transition Matrix)
- 각 열의 합이 1이 되도록 정규화됩니다
- 각 링크의 확률을 나타냅니다
- 열에서 행으로 나가는 링크 수로 나눕니다
A B C
A 0 0 1/2
B 1 0 1/2
C 0 1 0주요 차이점:
1. 값의 의미
- 인접행렬: 단순 연결 여부 (0 또는 1)
- 전이행렬: 전이 확률 (0~1 사이 값)
-
열의 합
- 인접행렬: 해당 노드의 외부 링크 수
- 전이행렬: 항상 1 (확률의 합이므로)
-
계산방법
전이행렬 = 인접행렬의 각 열을 해당 열의 합으로 나눔
(단, 열의 합이 0인 경우 모든 요소에 1/n 할당)
따라서 페이지랭크에서는:
1. 먼저 인접행렬을 만들고
2. 이를 정규화하여 전이행렬을 얻은 후
3. 댐핑 팩터를 적용하여 최종 전이행렬을 계산합니다.
전이행렬을 사용하는 이유
- 확률 모델링
- 웹 서핑 행동을 확률적으로 모델링하기 위함
- 사용자가 한 페이지에서 다른 페이지로 이동할 확률을 표현
- 각 열의 합이 1이 되어 확률 해석이 가능
- 마르코프 체인 적용
- 웹 서핑을 마르코프 체인으로 모델링
- 현재 상태(현재 페이지)에서 다음 상태(다음 페이지)로의 전이 확률 계산
- 장기적인 페이지 방문 확률 계산 가능
- 수렴 보장
예시:
초기벡터 v = [1/3, 1/3, 1/3]
전이행렬 M =
A B C
A 0 0 1/2
B 1 0 1/2
C 0 1 0
반복 계산:
v1 = M × v
v2 = M × v1
v3 = M × v2
...- 이 과정을 반복하면 각 페이지의 최종 중요도(PageRank)로 수렴
- 공정한 순위 계산
- 링크 수가 많은 페이지의 영향력을 정규화
- 각 페이지가 가진 총 링크 수로 나누어 공정성 확보
예: C페이지가 A,B 두 곳에 링크하면 각각 1/2의 가중치 부여
- 댐핑 팩터 적용 가능
M' = d*M + (1-d)/n- 임의 페이지로 이동할 확률 고려
- 고립된 페이지 문제 해결
- 순환 구조에서의 함정 방지
결론적으로, 전이행렬은:
- 웹 구조를 확률적으로 해석
- 수학적으로 안정적인 계산 가능
- 공정한 순위 산출
이 가능하도록 하는 핵심 요소입니다.
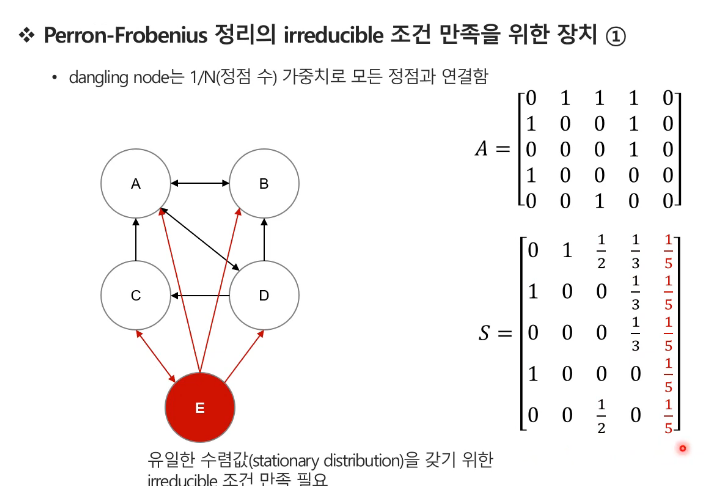
- 노드E는 나가는 엣지가 없다.
- irreducible하게 만들기 위해 1/n의 값을 e에 넣어준다.
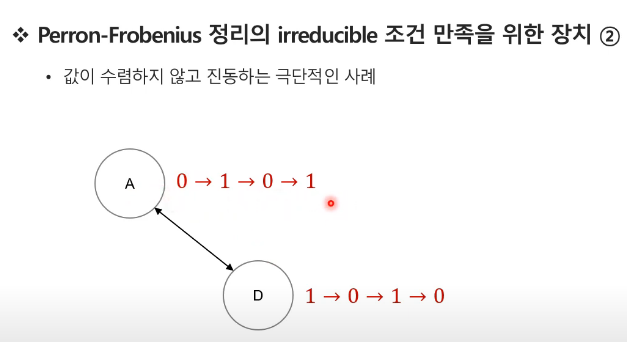
- 값이 진동하는 사례가 발생할 수도 있다.
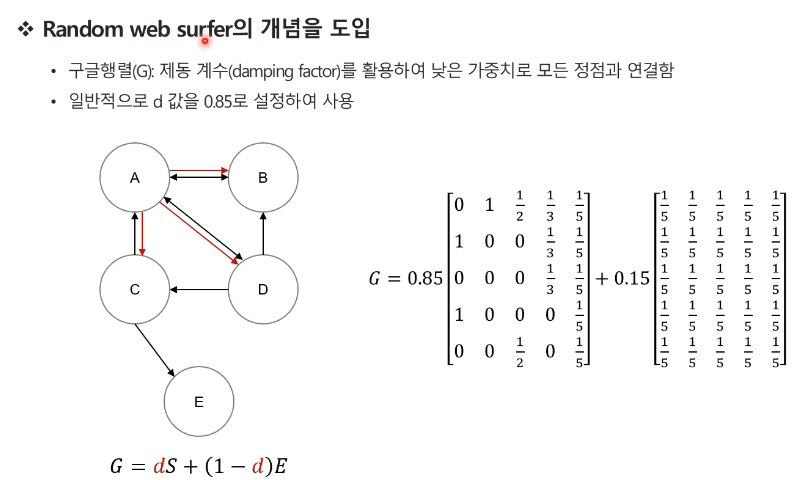
- 값이 수렴하지 않고 진동하는 사례들을 제거하기 위해 damping factor을 하용한다.
- 정의
- 보통 d로 표시하며, 0과 1 사이의 값
- 일반적으로 0.85(85%)를 사용
- 사용자가 현재 링크를 따라갈 확률
- 수식에서의 역할
M' = d*M + (1-d)/n
여기서:
M': 최종 전이행렬
M: 원래 전이행렬
d: 댐핑 팩터 (보통 0.85)
n: 전체 페이지 수- 실제 의미
- d (0.85): 사용자가 현재 페이지의 링크를 클릭할 확률
- (1-d) (0.15): 임의의 다른 페이지로 이동할 확률
- 필요한 이유
a) Dead End 문제 해결
A → B → C
↓
D- D는 외부 링크가 없는 Dead End
- 댐핑 팩터가 없으면 D의 PageRank가 0이 됨
b) Spider Trap 문제 해결
A → B → C
↑ ↓
D ← E ← F- 순환 구조에 빠지면 다른 페이지로 이동 불가
- 댐핑 팩터로 임의 이동 가능성 부여
- 예시 계산
3개 페이지(A,B,C)가 있을 때:
원래 전이행렬 M:
A B C
A 0 0 1/2
B 1 0 1/2
C 0 1 0
d = 0.85일 때 최종 전이행렬 M':
A B C
A 0.05 0.05 0.475
B 0.90 0.05 0.475
C 0.05 0.90 0.05- 효과
- 그래프를 Irreducible하게 만듦
- 모든 페이지가 최소 (1-d)/n의 방문 확률 보장
- PageRank 값의 안정적 수렴 보장
- 더 현실적인 웹 서핑 모델링
- 선택 기준
- d가 너무 작으면: 링크 구조의 중요성이 감소
- d가 너무 크면: Dead End와 Spider Trap 문제 해결이 어려움
- 0.85가 경험적으로 좋은 성능을 보임
이러한 댐핑 팩터는 PageRank 알고리즘의 핵심 요소로, 알고리즘의 안정성과 현실성을 높여주는 역할.
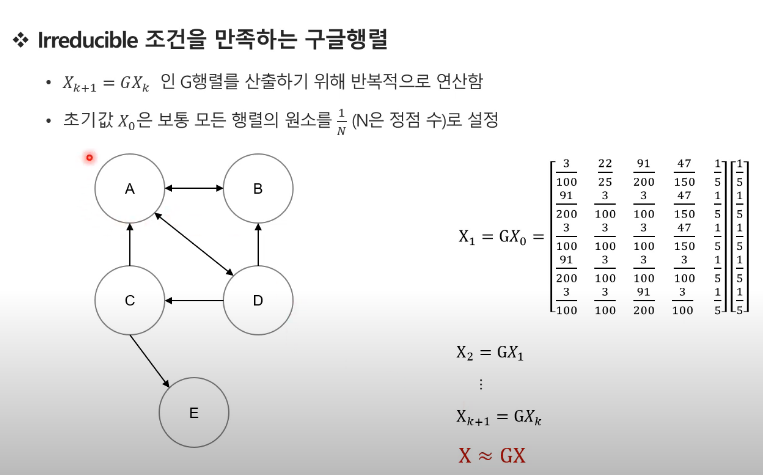
- Xi의 값을 G에 곱한 값을 또 다시 G랑 곱한다.
- 이를 반복하면 결국 X=GX로 수렴되는 X값이 나옴.
- 최종 수렴되는 X값을 Page Rank라고 한다.
