비츠앤바이츠(Bits and Bytes) 양자화

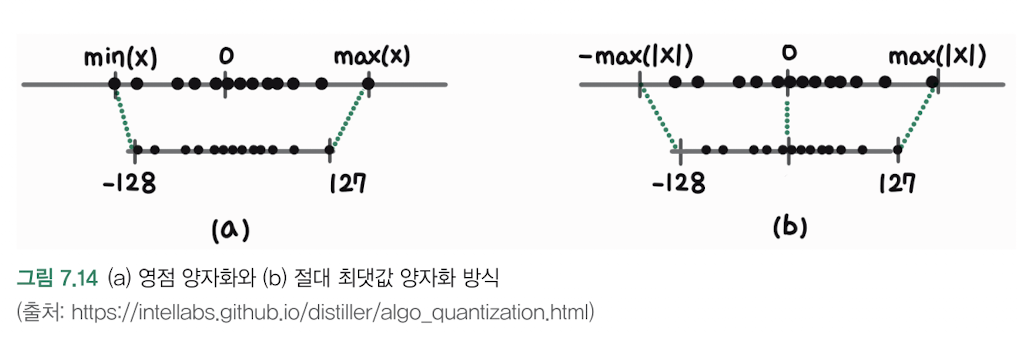
1. 영점 양자화 (Zero-point Quantization)

실제 예시: 가중치 데이터 [-2.731, -1.245, 0.012, 1.367, 2.892]

1) 데이터 분석:

• 최솟값(min): -2.731
• 최댓값(max): 2.892
• 영점(0)의 위치가 중요

2) 양자화 수식:

양자화값 = round((원본값 - 최솟값) × 255 ÷ (최댓값 - 최솟값))

3) 각 값의 변환:

-2.731 -> 0    (최솟값)
-1.245 -> 67   (((-1.245) - (-2.731)) × 255 ÷ 5.623 = 67)
 0.012 -> 124  ((0.012 - (-2.731)) × 255 ÷ 5.623 = 124)
 1.367 -> 186  ((1.367 - (-2.731)) × 255 ÷ 5.623 = 186)
 2.892 -> 255  (최댓값)

2. 절대 최댓값 양자화 (Absmax Quantization)

실제 예시: 같은 데이터 사용

1) 데이터 분석:

• 절대값 중 최댓값: max(|-2.731|, |2.892|) = 2.892
• 대칭 범위: [-2.892, 2.892]

2) 양자화 수식:

양자화값 = round((원본값 + 절대최댓값) × 255 ÷ (2 × 절대최댓값))

3) 각 값의 변환:

-2.731 -> 3    ((-2.731 + 2.892) × 255 ÷ 5.784 = 3)
-1.245 -> 71   ((-1.245 + 2.892) × 255 ÷ 5.784 = 71)
 0.012 -> 127  ((0.012 + 2.892) × 255 ÷ 5.784 = 127)
 1.367 -> 186  ((1.367 + 2.892) × 255 ÷ 5.784 = 186)
 2.892 -> 255  ((2.892 + 2.892) × 255 ÷ 5.784 = 255)

두 방식의 주요 차이점:

1. 영점 양자화:

• 장점:
  • 실제 데이터의 분포를 그대로 반영
  • 데이터의 범위를 최대한 활용
• 단점:
  • 양수와 음수의 표현 범위가 비대칭일 수 있음

2. 절대 최댓값 양자화:

• 장점:
  • 양수와 음수의 표현 범위가 항상 대칭
  • 0을 중심으로 균형잡힌 표현
• 단점:
  • 데이터가 한쪽으로 치우친 경우 범위 낭비 발생

예를 들어 실제 계산 과정을 더 자세히 보여드리면:

영점 양자화에서 0.012를 변환할 때:

1) 전체 범위 계산: 2.892 - (-2.731) = 5.623
2) 0.012에서 최솟값을 뺌: 0.012 - (-2.731) = 2.743
3) 255를 곱함: 2.743 × 255 = 699.465
4) 전체 범위로 나눔: 699.465 ÷ 5.623 = 124.46
5) 반올림: 124

절대 최댓값 양자화에서 0.012를 변환할 때:

1) 절대 최댓값 확인: 2.892
2) 전체 범위 계산: 2 × 2.892 = 5.784
3) 값에 절대최댓값을 더함: 0.012 + 2.892 = 2.904
4) 255를 곱함: 2.904 × 255 = 740.52
5) 전체 범위로 나눔: 740.52 ÷ 5.784 = 127.99
6) 반올림: 127

역양자화(복원) 과정도 비교해보면:

영점 양자화의 역양자화:

복원값 = (양자화값 × (최댓값 - 최솟값) ÷ 255) + 최솟값
124의 경우: (124 × 5.623 ÷ 255) - 2.731 = 0.013

절대 최댓값 양자화의 역양자화:

복원값 = (양자화값 × (2 × 절대최댓값) ÷ 255) - 절대최댓값
127의 경우: (127 × 5.784 ÷ 255) - 2.892 = 0.011

이처럼 두 방식 모두 약간의 오차는 있지만, 원본 값의 특성을 잘 보존하면서 데이터를 압축할 수 있습니다.

---

이상치

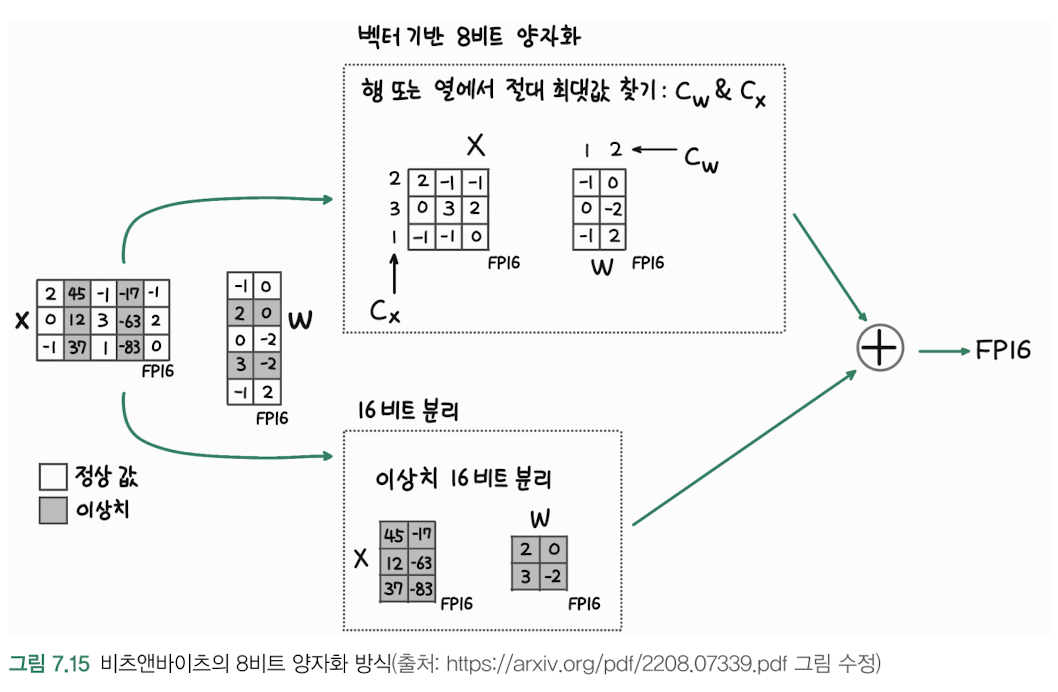
예시 데이터:

X 행렬 원본값:
[2    256  -1    -512  -1]     첫 번째 행
[0    12    3    -63   2]      두 번째 행
[-1   37    768  -83   0]      세 번째 행

1. 이상치 판단 과정:
   8비트로 표현 가능한 범위는 -128 ~ 127입니다.
   따라서 이 범위를 벗어나는 값들이 이상치입니다:

이상치들:
256  (첫 번째 행): 127 초과
-512 (첫 번째 행): -128 미만
768  (세 번째 행): 127 초과

2. 데이터 분리:

정상값 행렬(8비트로 표현):
[2    *    -1    *     -1]
[0    12    3   -63    2]
[-1   37    *   -83    0]

이상치 행렬(16비트로 표현):
256, -512, 768

3. 양자화 과정:
   정상값(8비트) 양자화 예시:

2 → 00000010
12 → 00001100
37 → 00100101
-83 → 10101101

이상치(16비트/FP16) 저장 예시:

256 → 0100011100000000
-512 → 1100100000000000
768 → 0100100100000000

4. 실제 저장 구조:

X 행렬의 최종 저장 형태:

[2(8bit)  256(16bit)  -1(8bit)  -512(16bit)  -1(8bit)]
[0(8bit)  12(8bit)    3(8bit)   -63(8bit)    2(8bit)]
[-1(8bit) 37(8bit)    768(16bit) -83(8bit)   0(8bit)]

5. 메모리 사용량 비교:

원본 데이터(모두 32비트):
15개 값 × 32비트 = 480비트

양자화 후:
정상값(8비트): 12개 × 8비트 = 96비트
이상치(16비트): 3개 × 16비트 = 48비트
총 144비트 (약 70% 메모리 절약)

이렇게 함으로써:
1. 대부분의 값은 8비트로 저장하여 메모리를 절약
2. 이상치는 16비트로 저장하여 정확도 유지
3. 전체 메모리 사용량을 크게 줄이면서도 중요한 값들의 손실을 방지