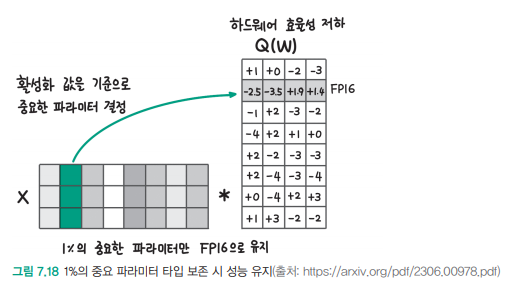
- AWQ의 기본 개념
- AWQ는 2023년 MIT에서 개발한 LLM 압축과 가속을 위한 양자화 기법입니다
- 모델의 성능을 최대한 유지하면서 특별히 중요한 파라미터의 정보를 보존하는 방식입니다
- 주요 특징과 작동 방식
- 활성화 값을 기준으로 상위 1%에 해당하는 모델 파라미터를 찾고, 해당 파라미터는 FP16으로 유지합니다
- 이미지에서 보여지는 것처럼 행렬 연산에서 특정 채널의 파라미터가 중요도에 따라 다르게 처리됩니다
- 그림 7.18에서 보여지듯이, 중요한 파라미터가 있는 영역은 녹색으로 표시되어 있습니다
- 구체적인 양자화 과정
- 첫 번째 단계: 중요한 파라미터 선별 (그림 7.18 참조)
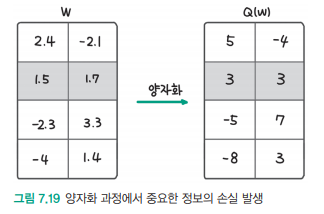
- 두 번째 단계: 선별된 파라미터에 대한 양자화 수행
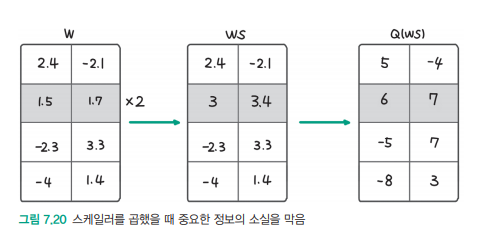
- 스케일러 값 적용: 그림 7.20에서 보여지듯이 스케일러를 곱하는 방식으로 중요 정보를 보존

- 실험 결과와 성능
- 표 7.1에서 보여지듯이, 스케일러 s값에 따른 성능 비교가 가능합니다
- s=2일 때 11.92의 성능을 보여주며, 이는 효과적인 압축률을 달성했음을 의미합니다
- AWQ의 장점
- 중요한 파라미터만 선별적으로 보존하여 효율적인 메모리 사용
- 모델의 중요한 특성을 유지하면서도 효과적인 압축 달성
- 실제 구현에서 성능 저하를 최소화
이러한 AWQ 방식은 특히 대형 언어 모델의 효율적인 배포와 실행에 매우 중요한 기술로, 제한된 리소스에서도 모델의 성능을 최대한 보존할 수 있게 해줍니다.
예시
1. 먼저 트랜스포머 모델의 한 레이어를 예시로 들어보겠습니다.
입력 텍스트: "고양이"
Step 1) 토큰화
"고양이" → ['고', '양', '이']
Step 2) 임베딩
각 토큰은 벡터로 변환됩니다. 간단히 4차원 벡터로 예시를 들어보겠습니다.
'고' → [1.0, 0.2, -0.3, 0.8]
'양' → [0.5, 1.1, 0.7, -0.4]
'이' → [-0.2, 0.9, 0.4, 0.6]
Step 3) 원본 가중치 행렬 (W)
이 임베딩 벡터들은 가중치 행렬과 곱해집니다. 예를 들어:
W = [
[2.7, -1.4, 0.9, -0.3],
[1.5, 0.8, -1.2, 2.1],
[-0.6, 1.7, 0.4, -0.9],
[1.1, -0.5, 2.3, 0.7]
]Step 4) 활성화 값 (A) 계산
'고' 벡터와 가중치 행렬을 곱하면:
[1.0, 0.2, -0.3, 0.8] × W = [1.2, 0.8, 0.3, 1.5]이것이 바로 활성화 값 A입니다.
2. 이제 AWQ 양자화를 적용해보겠습니다.
Step 1) 영향도(I) 계산
수식: I = |A × W|
예시로 첫 번째 원소:
|1.2 × 2.7| = 3.24
모든 원소에 대해 계산:
I = [3.24, 1.12, 0.27, 0.45]
Step 2) 스케일 팩터(s) 결정
영향도가 높은 가중치는 더 정밀한 양자화가 필요합니다.
예를 들어 s = 0.5로 정했다면:
원본 가중치 2.7의 양자화:
1) 2.7/0.5 = 5.4
2) round(5.4) = 5
3) 5 × 0.5 = 2.5
이것이 양자화된 가중치가 됩니다.
3. 비트 할당
영향도에 따라 다른 비트 수를 할당합니다:
영향도: 3.24 → 5비트
영향도: 1.12 → 4비트
영향도: 0.27 → 2비트
영향도: 0.45 → 3비트실제 결과를 시각화하면:
정밀도
5비트 - *
4비트 - *
3비트 - *
2비트 - *
+-------------------->
W1 W2 W3 W4이렇게 함으로써:
- 중요한 가중치(영향도가 높은)는 더 정밀하게 저장
- 덜 중요한 가중치는 더 큰 압축률 적용
- 전체적인 모델 성능은 유지하면서 모델 크기 감소
실생활의 예시
1. 동전 분류 상자:
- 500원: 정밀한 구멍(큰 가치, 중요)
- 100원: 중간 크기 구멍
- 10원: 덜 정밀한 구멍(작은 가치, 덜 중요)
AWQ도 이와 비슷합니다. 중요한 정보는 정밀하게, 덜 중요한 정보는 덜 정밀하게 저장합니다.
2. 실제 예시를 들어보겠습니다.
한글 "나"를 컴퓨터가 이해하는 과정:
Step 1) 먼저 "나"를 숫자로 변환
"나" → [1.5, -0.8, 2.3, 0.4]
Step 2) 이 숫자들이 신경망을 통과할 때 사용되는 가중치
원본 가중치(W):
W1 = 2.7 (매우 중요한 가중치)
W2 = -1.4 (중요한 가중치)
W3 = 0.9 (덜 중요한 가중치)
W4 = -0.3 (가장 덜 중요한 가중치)Step 3) 활성화 계산
"나"의 벡터와 가중치를 곱합니다:
1.5 × 2.7 = 4.05 (큰 영향)
-0.8 × -1.4 = 1.12 (중간 영향)
2.3 × 0.9 = 2.07 (작은 영향)
0.4 × -0.3 = -0.12 (아주 작은 영향)Step 4) AWQ 적용
큰 영향을 주는 가중치는 더 정밀하게 저장:
W1(2.7)의 경우:
- 5비트 사용
- 더 정밀한 저장 가능
- 2.7 → 2.75 (아주 작은 오차)
W4(-0.3)의 경우:
- 2비트만 사용
- 덜 정밀하게 저장
- -0.3 → -0.25 (좀 더 큰 오차 허용)
실제 변환 과정을 보여드리면:
1. W1 = 2.7 (중요함)
원본: 2.7
5비트 사용: 10110
실제 저장값: 2.75
오차: 0.052. W4 = -0.3 (덜 중요함)
원본: -0.3
2비트 사용: 11
실제 저장값: -0.25
오차: 0.05이렇게 하면:
- 중요한 정보(W1)는 거의 그대로 보존
- 덜 중요한 정보(W4)는 조금 뭉뚱그려서 저장
- 전체 저장 공간은 크게 절약
- 모델의 성능은 거의 유지
이것이 AWQ의 핵심입니다. 마치 중요한 물건은 좋은 상자에, 덜 중요한 물건은 간단한 상자에 넣는 것처럼, 가중치의 중요도에 따라 다른 정밀도로 저장하는 것입니다.
