1. DeepWalk

1.1 핵심 아이디어

DeepWalk는 자연어 처리의 Word2Vec 아이디어를 그래프에 적용한 것입니다. 그래프의 노드들을 단어처럼 생각하고, 랜덤 워크로 생성된 노드 시퀀스를 문장처럼 간주합니다.

1.2 간단한 예시

다음과 같은 소셜 네트워크가 있다고 가정해보겠습니다:

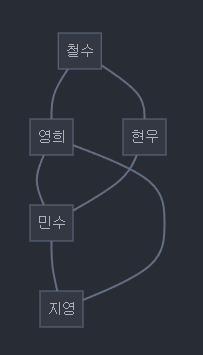
1.3 랜덤 워크 생성

이 그래프에서 가능한 랜덤 워크의 예시:

• 철수 → 영희 → 민수 → 지영
• 철수 → 현우 → 민수 → 영희
• 영희 → 민수 → 현우 → 철수

1.4 목적 함수

DeepWalk의 목적 함수는 다음과 같습니다:

maximize Σ log P(vi+j | vi)

여기서:

• vi는 현재 노드
• vi+j는 컨텍스트 윈도우 내의 주변 노드
• P(vi+j | vi)는 소프트맥스 함수로 계산됨

실제 수식으로는:

P(vi+j | vi) = exp(u'ᵀvi) / Σ exp(u'ᵀvk)

• u'는 컨텍스트 노드의 임베딩 벡터
• v는 중심 노드의 임베딩 벡터
• k는 모든 가능한 노드

2. Node2Vec

2.1 DeepWalk와의 차이점

Node2Vec은 DeepWalk를 개선한 버전으로, 두 가지 파라미터를 추가했습니다:

• p (Return parameter): 이전 노드로 돌아갈 확률 조절
• q (In-out parameter): BFS와 DFS의 균형을 조절

2.2 예시로 보는 파라미터의 영향

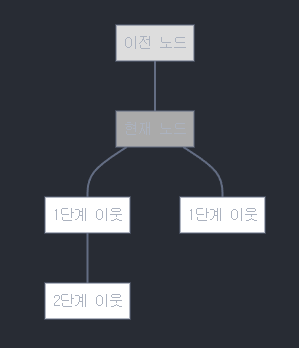
위 그래프에서:

• p가 작을 때: 이전 노드(T)로 돌아갈 확률 증가
• p가 클 때: 이전 노드로 돌아가지 않음
• q가 작을 때: 2단계 이웃(C)으로 갈 확률 증가 (DFS 성향)
• q가 클 때: 1단계 이웃(A,B)에 머무를 확률 증가 (BFS 성향)

2.3 Node2Vec 목적 함수

기본적인 목적 함수는 DeepWalk와 같지만, 랜덤 워크 생성 과정이 다릅니다:

maximize Σ log P(N(u) | u)

여기서:

• N(u)는 노드 u의 네트워크 이웃
• 각 이웃으로 이동할 확률은 p,q 값에 따라 결정됨

실제 전이 확률:

P(x → y) ∝ 
    1/p   (d = 0, 이전 노드로)
    1     (d = 1, 1단계 이웃으로)
    1/q   (d = 2, 2단계 이웃으로)

3. 실제 적용 예시

소셜 네트워크에서:
1. DeepWalk

• 친구 추천: 비슷한 임베딩을 가진 노드끼리 연결 제안
• 커뮤니티 탐지: 임베딩 공간에서 클러스터링

2. Node2Vec

• p값을 작게: 같은 커뮤니티 내 멤버 발견에 유용
• q값을 작게: 다른 커뮤니티와의 연결고리 발견에 유용

---

p, q 파라미터

일반적으로 Node2Vec의 p, q 값은 다음과 같이 설정됩니다:

일반적인 p, q 값 조합

1. 균형잡힌 탐색 (기본값)

• p = 1, q = 1
  • DeepWalk와 동일한 동작
  • 특별한 이유가 없다면 이 값으로 시작하는 것을 추천

2. 구조적 동질성 (Structural Equivalence) 중시

• p = 1, q = 0.5
  • 노드의 역할/구조적 유사성 탐색에 좋음
  • 예: 회사 조직도에서 "과장" 직급처럼 비슷한 역할을 하는 노드 찾기

3. 커뮤니티 중심 (Homophily)

• p = 0.25, q = 2
  • 같은 커뮤니티 내의 노드들을 찾는데 효과적
  • 예: SNS에서 같은 동호회 멤버 찾기

실제 예시로 보는 파라미터 효과

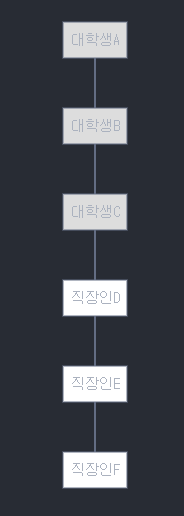
위 그래프에서:

1. p=1, q=1 (균형)

• 대학생과 직장인 그룹을 골고루 탐색

2. p=1, q=0.5 (구조적)

• C와 D처럼 서로 다른 그룹을 연결하는 "브릿지" 역할의 노드 발견에 유용

3. p=0.25, q=2 (커뮤니티)

• 대학생 그룹(A,B,C)이나 직장인 그룹(D,E,F) 내부를 집중적으로 탐색

파라미터 선택 팁

1. 그리드 서치 추천 범위:

• p: [0.25, 0.5, 1, 2, 4]
• q: [0.25, 0.5, 1, 2, 4]

2. 상황별 초기값 추천:

• 커뮤니티 탐색: p=0.25, q=2
• 구조적 역할 탐색: p=1, q=0.5
• 일반적인 탐색: p=1, q=1

3. 검증 방법:

• 노드 분류 정확도
• 링크 예측 성능
• 클러스터링 품질 지표

실제로는 데이터셋의 특성과 목적에 따라 이 값들을 조정해가며 최적의 조합을 찾는 것이 좋습니다. 특히 처음에는 기본값(p=1, q=1)으로 시작해서 점진적으로 조정하는 것을 추천드립니다.