AI Math 추가정리) MLE, MAP 정리

함수표기법( ; 와 | 의 차이)

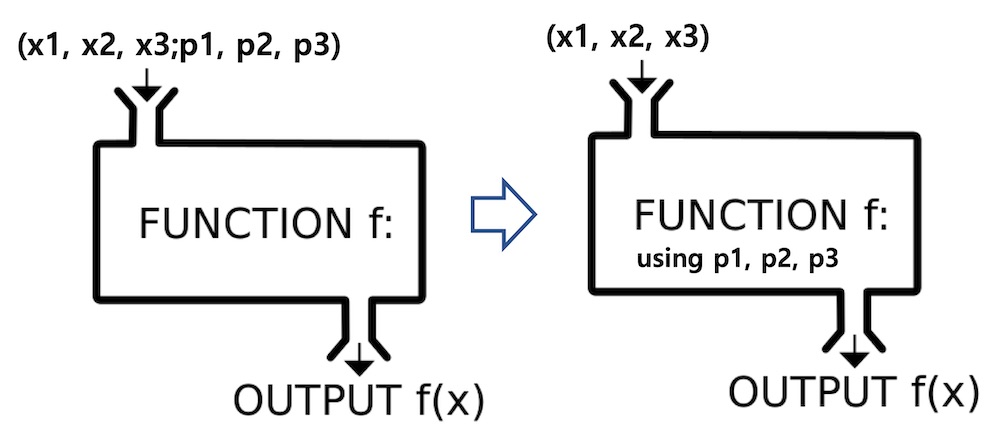
• | : 조건부확률 표기할 때
• ; : 함수의 parameter를 나타냄
• 출처: http://taewan.kim/post/function_in_semicolon/
• 확률변수와 확률분포의 관점에서 보았을 때: https://blog.naver.com/kyoungblee/222460452018

---

모수와 표본

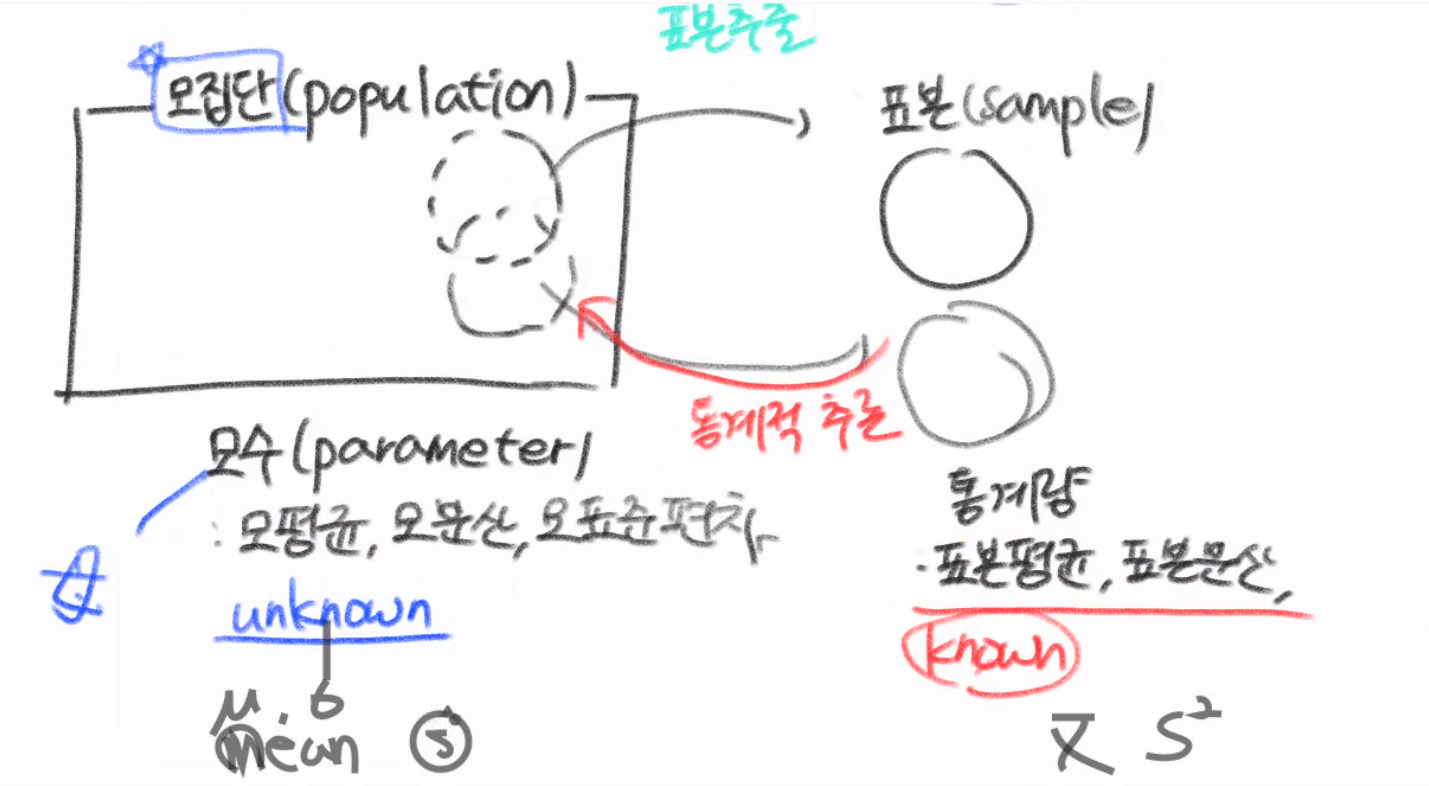
• 모집단(popilation): 관측 대상이 되는 전체 집단
  • 모수(parameter): 모평균, 모표준편차, 모분산등 모집단의 데이터
    • 모평균: $\mu$
    • 모분산: $\sigma^2$
    • 모표준편차: $\sigma$

• 표본(sample): 모집단의 부분집합
  • 표본 통계량(sample statistic): 표본에 의존하는 통계량
    • 표본평균: ${\displaystyle {\bar {X}}}$
    • 표본분산: $S^2$
    • 표본표준편차: $S$

---

확률변수(Random Variable)

확률변수 $X$는 이산(discrete)일 경우 확률질량함수, 연속(continuous)일 경우 확률밀도함수라고 부른다.

• $x$: $X$가 취할 수 있는 값
• $\theta$: 확률밀도함수의 모수
  • 둘 다 scalar, vector 가능

---

최대가능도 추정법(MLE, Maximum Likelihood Estimation)

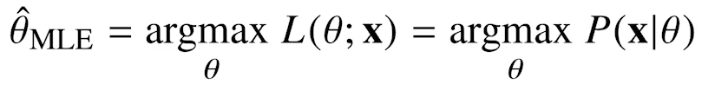
1. 모수추정에서는 $x$(어떤 분포에 대해 나올 수 있는 확률밀도, 상수벡터)를 알고, $\theta$(변수벡터)를 모른다.

   $L(θ;x) = fx(x;\theta) = p(x;\theta)$

2. 복수의 표본값에 대한 결합확률밀도

   $p(x;θ)=p(x_1,x_2,⋯,x_n;θ)$

3. $x_1, x_2, ... x_n$은 $i.i.d$이기 때문에 결합확률밀도함수는 독립사건의 확률 계산에 의해 다음처럼 곱으로 표현된다

   $P(x|\theta) = \prod_{k=1}^{n}P(x_k|\theta)$

4. 위 식의 결과값이 가장 커지는 $\theta$를 모수의 추정값 $\hat\theta$
   여러 개의 표본 데이터가 있는 경우에 대해, 이 식을 likelihood function이라고 하고 보통은 자연로그를 취하여 아래와 같이 log-likelihood function $L(θ|x)$ 를 이용

• $L(θ;x)$
  • 가능도함수, likelihood
  • 주어진 데이터 x에 대해, 모수(parameter) $θ$를 변수로 둔 함수
    데이터가 주어져있는 상황에서, $θ$를 변형시킴에 따라 값이 바뀌는 함수
  • 모수 θ를 따르는 분포가 데이터 $x$를 관찰할 가능성
• $P(x|θ)$
  • 확률밀도(질량)함수
  • $θ$가 주어져있을 때 $x$에 대한 함수
• 둘이 같은건 정의에 의해서인지??
  • 가능도 $L(\theta;x)$의 경우 θ를 따르는 확률분포에서 $x$가 가지는 확률(밀도),
  • $f(x|\theta)$는 사건 $θ$일 때 $x$일 확률(밀도)
    로 값이 동일하겠지만 보는 초점이 달라 가능도는 주어진 x에 대한 θ의 함수, 뒤의 확률분포는 주어진 $θ$에 $x$의 함수 정도의 차이가 있습니다.

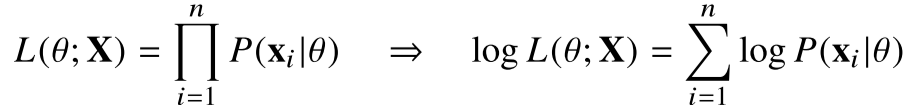
• 만약 데이터 집합 X가 i.i.d일 경우(독립적으로 추출되었을 경우)
  L(θ;x)은 각 P(x|θ)의 곱(각 사건이 일어날 가능성의 곱)으로 나타낼 수 있다
  --> 이것도 정의에 의해서인지?
  ----> 독립이기 때문에!!
• 양변에 log를 씌우면 log-likelihood는 log-확률분포들의 덧셈으로 표현 가능
  --> 연산량을 O(n2)에서 O(n)으로 줄일 수 있음

중간정리

• 데이터 집합 X(x1, x2, ... xn)가 i.i.d.일 경우에만
• 출처: https://m.blog.naver.com/sw4r/221972663841

---

최대사후확률 추정법(MAP, Maximum a Posteriori)

• MLE의 단점(observation에 따라 값이 너무 민감하게 변함)을 해결하기 위해 사용

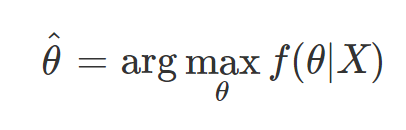
• 여기서 f(θ|x)는 P(θ|x)와 동일
• θ가 주어지고, 그 θ에 대한 데이터들의 확률을 최대화하는 것이 아니라, 주어진 데이터에 대해 최대 확률을 가지는 θ를 찾는다
• MAP를 계산하기 위해서는 f(x|θ), posteriori가 필요하지만 우리가 아는건 f(θ|x), likelihood뿐
  --> Bayer's theorem 이용

Bayer's theorem

• P(θ|X), posterior: 주어진 데이터에 대한 현상의 확률
  data를 관찰했을 때, 이 parameter(θ)가 성립할 확률, 측정 이후의 확률이기 때문

• P(X|θ), likelihood: observation
  현재 주어진 parameter에서 이 data가 관찰될 확률, 사전확률이 없을 경우 분석하기 어렵다. 임의로 설정하는 경우도 있음.

• P(θ), prior: 현상에 대한 사전정보
  prior distribution, data에 대해 측정하기 전에 가정한 확률

• P(X), evidence: data 전체의 분포

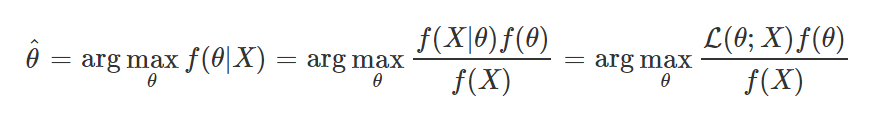
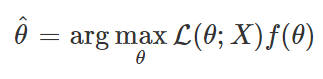
• P(X)는 θ에 대한 식이 아니기 때문에 생략 가능
• 따라서 P(θ)를 알고있다면 MLE 대신 MAP를 사용하는 것이 가능
  --> θ에 대한 사전정보(assumption)을사용해 결과를 향상시킬 수 있다

• 출처: http://sanghyukchun.github.io/58/