Supervised vs Unsupervised

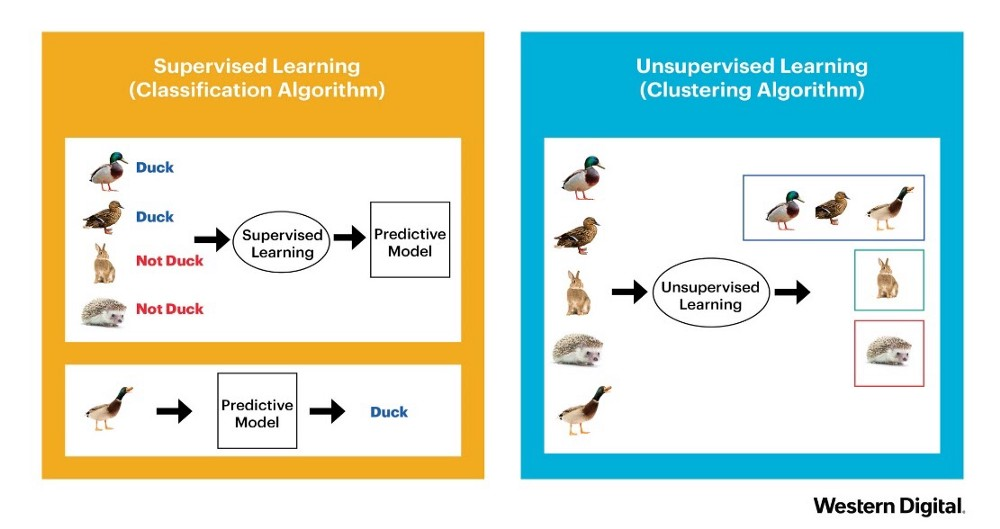
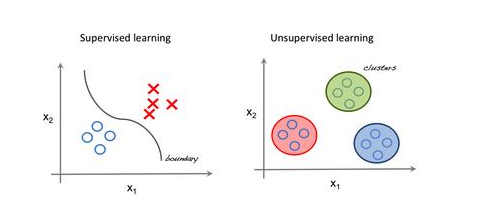
• Supervised learning

  • Dataset이 x-y 쌍(Input data - Ground truth)으로 구성
  • Classification, Regression

• Unsupervised learning

  • Dataset에 오직 input data만 존재
  • Clustering, Association rule

---

Clustering

Data point set을 기준으로 비지도적으로 분류하기 위한 것.
같은 그룹 안에 속한 data points는 특징과 비슷한 속성을 갖고 있어야 하지만 다른 그룹에 속하는 data points는 특징과 비슷하지 않은 속성을 가져야 한다.

• 모델의 종류
  • K-means
  • Mean-shift
  • DBSCAN
  • GMM
  • Agglomerative Hierarchical Clustering

K-means

알고리즘 단계

1. 클래스 혹은 그룹의 수(K)를 정해야 한다. 그러면 그 숫자에 따라 랜덤하게 center point를 잡는다.
2. 각 data point는 각 center point끼리의 거리를 측정해서 분류된다.
3. 분류된 data points에 기반해서 우리는 모든 그룹의 벡터의 평균(mean)을 구하는 것으로 그룹의 center를 recompute한다.
4. 이 과정을 그룹 center가 그렇게까지 많이 바뀌지 않는 선에서 반복한다. 물론 그룹 center를 랜덤하게 여러번 초기화 시킬 수 있고 가장 좋은 결과가 나오도록 고를 수도 있다.

예시

장점과 단점

장점

1. 단순성과 이해 용이성: k-means는 이해하고 구현하기 쉬운 알고리즘으로, 기본적인 아이디어는 간단하며, 각 단계는 직관적
2. 빠른 실행 속도: k-means는 비교적 빠르게 실행됨. 일반적으로 $O(n \cdot k \cdot t)$의 시간 복잡도를 가지며, 여기서 $n$은 데이터 포인트 수, $k$는 클러스터 수, $t$는 반복 횟수
3. 효율성 큰 데이터셋에서도 효율적으로 작동하며, 적절한 초기화와 최적화 기술을 사용하면 매우 빠르게 수렴
4. 다양한 응용 분야: 고객 세분화, 이미지 압축, 패턴 인식 등 다양한 응용 분야에서 사용됨
5. 구현의 용이성: 여러 프로그래밍 언어와 머신러닝 라이브러리에서 k-means 알고리즘을 쉽게 사용할 수 있음

단점

1. 클러스터 수(k)의 사전 지정 필요: 클러스터 수를 미리 지정해야함
2. 구형 클러스터 가정: k-means는 구형(또는 원형) 클러스터를 가정하기 때문에 비구형 클러스터가 있는 데이터에서는 적절히 작동하지 않을 수 있음
3. 초기화에 민감함: 초기 클러스터 중심의 선택에 따라 결과가 달라질 수 있어, 적절하지 않은 초기 중심 선택은 지역 최적값에 빠지게 할 수 있고, 매 run마다 결과가 달라질 수 있음
4. 노이즈와 이상치에 민감함: k-means는 노이즈와 이상치에 민감함. 이상치가 클러스터 중심으로 선택되면 클러스터링 결과가 왜곡될 수 있음
5. 클러스터 크기 불균형 문제: k-means는 크기와 밀도가 다른 클러스터를 잘 처리하지 못함. 큰 클러스터는 작은 클러스터를 압도할 수 있음
6. 데이터 스케일에 민감함: 변수의 크기나 범위가 다른 경우, 데이터 스케일링(정규화 또는 표준화)을 사전에 수행하지 않으면 성능이 저하될 수 있음

* K-median: mean을 구할때 그룹의 median을 이용

K-NN vs K-means

• K-NN: 주변 k개의 data를 참고하여 해당 data의 label을 결정
• K-means: 전체 data를 k개의 group으로 분류

Mean-shift

• K-means와 비슷하나, 확률 밀도 중심 내에서 data의 확률 밀도가 높은 곳으로 이동(centroid-based algorithm, hill-climbing algorithm)
• 확률 밀도를 찾기 위해 KDE(Kernel density estimation)을 이용
• K-means와 다르게 bandwidth 크기에 따라 자동으로 group 개수를 최적화. 하지만 kernel size(이미지 상 sliding window의 radius)를 설정해야함
• Computer vision에서는 object tracking에 사용

알고리즘 단계

1. 개별 데이터의 특정 반경 내에 주변 데이터를 포함한 데이터 분포도를 KDE 이용하여 계산
2. KDE로 계산된 데이터 분포도가 높은 방향으로 데이터 이동
3. 모든 데이터를 1-2까지 수행하면서 데이터를 이동, 개별 데이터들이 군집 중심점에 모임
4. 지정된 반복만큼 전체 데이터에 대해 KDE 기반으로 데이터를 이동시키면서 군집화 수행
5. 개별 데이터들이 모인 중심점을 군집 중심점으로 설정

예시

--> 이후 새로운 $m_{new}$의 반경 h에 속하는 데이터 포인트로 다시 중심을 업데이트

장점과 단점

장점

1. 클러스터 수 사전 지정 불필요: 데이터의 밀도 분포에 따라 자동으로 클러스터 수를 결정하므로, 사전에 클러스터 수를 지정할 필요가 없음
2. 비구형 클러스터 감지: Mean-shift는 데이터의 밀도 피크를 찾는 방식으로 작동하기 때문에, 구형이 아닌 비구형 클러스터도 효과적으로 감지할 수 있음
3. 노이즈와 이상치 처리: 노이즈와 이상치가 클러스터 중심으로 선택될 가능성이 적으므로, 노이즈와 이상치에 대해 강인한 특성을 가짐
4. 단순성: 알고리즘의 개념이 단순하고
5. 높은 품질의 클러스터링: 밀도가 높은 영역을 중심으로 클러스터를 형성하기 때문에, 종종 매우 품질이 높은 클러스터링 결과를 제공

단점

1. 계산 비용: Mean-shift는 모든 데이터 포인트에 대해 커널 밀도 추정을 수행하므로 계산 비용이 높음. 특히 대규모 데이터셋에서는 비효율적일 수 있음
2. 밴드위스 선택: 알고리즘의 성능과 결과는 밴드위스(반경) 파라미터 $h$에 크게 의존. 적절한 $h$ 값을 선택하는 것이 어려울 수 있으며, 데이터에 따라 결과가 크게 달라질 수 있음
3. 고차원 데이터에서의 성능: 고차원 데이터에서는 밀도 추정이 어려워질 수 있으며, 커널 함수의 계산 비용이 증가
4. 경계 포인트 처리: 클러스터 경계에 있는 포인트들은 이동하는 중심에 의해 쉽게 분리되거나 결합될 수 있으며, 이는 클러스터의 경계가 명확하지 않게 만드는 요인이 될 수 있음
5. 메모리 사용량: 모든 데이터 포인트를 저장하고 처리해야 하기 때문에 메모리 사용량이 많아질 수 있음

KDE(Kernel density estimation)

밀도추정 (Density Estimation)

관측한 data들로부터 원래 변수의 (확률) 분포 특성을 추정하는 것

e.g. 최근 1년치 일일 교통량 데이터로 '일일 교통량'이라는 변수의 분포 특성을 추정

• f(x): 확률 밀도 함수(pdf, probabilty density function)
• x=a일 확률(probability)는 0 (discrete한 확률질량함수와 다르게 continuous한 실수의 분포이기 때문)
• 그러나 x=a에서의 밀도(density)는 f(a)로 0이 아님

• x가 a~b 사이의 값을 가질 확률은 그 구간에서의 확률밀도함수의 적분값(면적)으로 계산됨
  --> 밀도는 확률밀도함수의 함수값이며, density를 일정 구간에 대해 적분하면 해당 구간에 대한 확률을 구할 수 있음
• 따라서 어떤 변수의 pdf를 구할 수 있으면 그 변수가 가질 수 있는 값의 범위, 확률분포, 특성 등을 알 수 있음

Parametric vs. Non-parametric 밀도추정

• Parametric
  • 미리 pdf(probability density function)에 대한 모델을 정해놓고 데이터들로부터 모델의 파라미터만 추정하는 방식
  • 하지만 현실 세계의 문제에서는 분포의 모델이 미리 주어지는 경우는 거의 없음

• Non-parametric
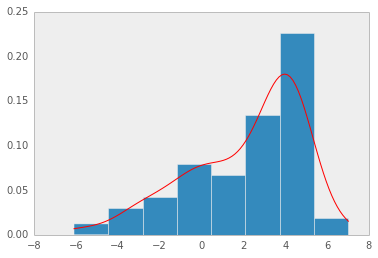
  • Histogram: 밀도추정의 가장 간단한 형태
  • 관측된 데이터들로부터 히스토그램을 구한 후 구해진 히스토그램을 정규화하여 확률밀도함수로 사용

KDE(Kernel density estimation)

히스토그램 방법은 bin의 경계에서 불연속성이 나타난다는 점, bin의 크기 및 시작 위치에 따라서 히스토그램이 달라진다는 점, 고차원(high dimension) 데이터에는 메모리 문제 등으로 사용하기 힘들다는 점 등의 문제점을 가짐

KDE는 kernel function을 이용해 히스토그램의 문제점을 개선

• Kernel function: 원점을 중심으로 좌우 대칭이면서 적분값이 1인 non-negative 함수로 정의되며 가우시언(Gaussian), Epanechnikov, uniform 함수 등이 대표적인 커널 함수

• h: kernel 함수의 bandwidth parameter로, 클수록 함수 형태가 완만해지고 작을수록 뾰족해짐

1. 관측된 데이터 각각마다 해당 데이터 값을 중심으로 하는 커널 함수를 생성한다: K(x-xi)
2. 이렇게 만들어진 커널 함수들을 모두 더한 후 전체 데이터 개수로 나눈다.

• 히스토그램 방법은 이산적(discrete)으로 각 데이터에 대응되는 bin의 값을 증가시킴으로써 불연속성이 발생하는 반면,
• KDE(커널밀도추정) 방법은 각 데이터를 커널 함수로 대치하여 더함으로써 오른쪽 그래프와 같이 smooth한 확률밀도함수(pdf)를 얻을 수 있는 장점을 가짐

즉, KDE(Kernel Density Estimation)를 통해 얻은 확률밀도함수는 히스토그램 확률밀도함수를 스무딩(smoothing)한 것으로도 볼 수 있으며 이 때, 스무딩(smoothing) 정도는 아래 그림처럼 어떤 bandwidth 값의 커널 함수를 사용했으냐에 따라 달라짐

DBSCAN

• 밀도 기반 클러스터링의 대표적인 알고리즘으로, 다양한 데이터셋에서 효과적으로 클러스터를 탐지할 수 있음
• 클러스터의 수를 사전에 지정할 필요가 없고, 데이터의 밀도 차이에 따라 클러스터를 자동으로 감지
• 노이즈나 이상치(Outlier)를 효과적으로 처리할 수 있음

주요 개념

• Epsilon (ϵ): 반경. 주어진 데이터 포인트에서 ϵ 거리 이내의 데이터 포인트들을 "이웃(neighbors)"이라고 함
• MinPts: 최소 포인트 수. 클러스터가 되기 위해 필요한 최소한의 데이터 포인트 수
• Core Point: 중심 포인트. ϵ 거리 내에 적어도 MinPts 이상의 이웃을 가진 데이터 포인트
• Border Point: 경계 포인트. ϵ 거리 내에 MinPts 미만의 이웃을 가지지만, 어떤 중심 포인트의 이웃에 포함되는 데이터 포인트
• Noise Point: 노이즈 포인트. ϵ 거리 내에 MinPts 미만의 이웃을 가지며, 어떤 클러스터에도 속하지 않는 데이터 포인트

알고리즘 단계

1. 초기화
   • 모든 데이터 포인트에 대해 방문 여부를 초기화합니다.
2. 포인트 방문
   • 데이터 포인트를 하나 선택하여 방문합니다.
   • 이 포인트가 이미 방문한 포인트라면 다음 포인트로 넘어갑니다.
3. 이웃 점검
   • 선택한 포인트의 $\epsilon$ 이웃들을 찾습니다.
   • 이웃들의 수가 MinPts 이상이면, 새로운 클러스터를 형성합니다.
   • 그렇지 않으면, 이 포인트는 노이즈로 간주될 수 있습니다.
4. 클러스터 확장
   • 새로운 클러스터가 형성되면, 이 클러스터에 포함된 모든 포인트에 대해 $$\epsilon$$ 이웃을 확인하여 클러스터를 확장합니다.
   • 각 이웃 포인트에 대해 다시 $\epsilon$ 이웃을 찾고, 이 과정은 더 이상 새로운 포인트가 추가되지 않을 때까지 반복됩니다.
5. 반복
   • 모든 포인트가 방문될 때까지 또는 모든 포인트가 클러스터에 할당될 때까지 위 과정을 반복합니다.

예시

장점과 단점

장점

• 클러스터 수를 사전에 지정할 필요가 없음
• 노이즈와 이상치(Outliers)를 효과적으로 처리할 수 있음
• 비구형 클러스터를 잘 탐지할 수 있음

단점

• 고차원 데이터에서 $\epsilon$과 MinPts의 적절한 값을 찾기 어려울 수 있음
• 밀도가 크게 다른 클러스터가 있는 데이터셋에서는 성능이 떨어질 수 있음

GMM, Gaussian Mixture Model

• 어떠한 데이터 분포가 여러 개의 Gaussian 분포 여러 개가 섞여서 만들어졌다고 생각하고, 해당 데이터 분포를 이루는 여러 개의 Gaussian 분포로 나타내는 확률적 생성 모델
• 다른 Clustering 모델과 달리, 해당 Cluster에 속할 확률을 같이 나타내주기 때문에, Clustering 결과에 불확실성도 함께 고려할 수 있음
• 확률을 포함한 Clustering이나, 데이터 생성, 이상치 탐지(다른 이상치 제거 알고리즘과 함께 사용되는 경우) 등에 유용하게 사용됨
• 초기값 설정에 매우 민감하기 때문에 K-mean와 같은 알고리즘을 이용해 초기값을 세팅함

구성 요소
1. 가우시안 분포 (Gaussian Distribution):

$\mathcal{N}(\mathbf{x} \mid \boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k) = \frac{1}{(2\pi)^{d/2} |\boldsymbol{\Sigma}_k|^{1/2}} \exp \left( -\frac{1}{2} (\mathbf{x} - \boldsymbol{\mu}_k)^\top \boldsymbol{\Sigma}_k^{-1} (\mathbf{x} - \boldsymbol{\mu}_k) \right)$

• 여기서 $\boldsymbol{\mu}_k$는 가우시안 분포 $k$의 평균 벡터, $\boldsymbol{\Sigma}_k$는 공분산 행렬

2. 혼합 계수 (Mixing Coefficients):

   • 각 가우시안 분포 $k$에 대한 혼합 계수 $\pi_k$는 해당 분포가 데이터 전체에서 차지하는 비율
   • $\sum_{k=1}^{K} \pi_k = 1$이며, $0 \leq \pi_k \leq 1$입니다.

3. 가우시안 혼합 모델 (GMM):

   • GMM은 여러 가우시안 분포의 혼합으로, 데이터 포인트 $\mathbf{x}$의 확률 밀도 함수는 다음과 같이 정의:
     $p(\mathbf{x}) = \sum_{k=1}^{K} \pi_k \mathcal{N}(\mathbf{x} \mid \boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k)$

알고리즘 단계

GMM의 매개변수 $\boldsymbol{\pi}, \boldsymbol{\mu}, \boldsymbol{\Sigma}$는 주어진 데이터에 맞게 최적화. 이때 Expectation-Maximization (EM)이 주로 사용됨

1. 초기화:

   • $\boldsymbol{\pi}, \boldsymbol{\mu}, \boldsymbol{\Sigma}$의 초기 값을 설정합니다.

2. E-step (Expectation Step):

   • 현재 매개변수를 사용하여 각 데이터 포인트가 각 가우시안 분포에 속할 확률(책임도, responsibility) $\gamma(z_{ik})$를 계산합니다:
     $\gamma(z_{ik}) = \frac{\pi_k \mathcal{N}(\mathbf{x}_i \mid \boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k)}{\sum_{j=1}^{K} \pi_j \mathcal{N}(\mathbf{x}_i \mid \boldsymbol{\mu}_j, \boldsymbol{\Sigma}_j)}$
   • 여기서 $\gamma(z_{ik})$는 데이터 포인트 $\mathbf{x}_i$가 가우시안 분포 $k$에서 생성될 확률입니다.

3. M-step (Maximization Step):

   • 책임도 $\gamma(z_{ik})$를 사용하여 매개변수를 업데이트합니다:
     $\pi_k = \frac{N_k}{N}, \quad \boldsymbol{\mu}_k = \frac{1}{N_k} \sum_{i=1}^{N} \gamma(z_{ik}) \mathbf{x}_i, \quad \boldsymbol{\Sigma}_k = \frac{1}{N_k} \sum_{i=1}^{N} \gamma(z_{ik}) (\mathbf{x}_i - \boldsymbol{\mu}_k)(\mathbf{x}_i - \boldsymbol{\mu}_k)^\top$
   • 여기서 $N_k = \sum_{i=1}^{N} \gamma(z_{ik})$는 클러스터 $k$에 할당된 데이터 포인트의 총 책임도입니다.

4. 반복:

   • E-step과 M-step을 매개변수가 수렴할 때까지 반복합니다.

Intuition

1. 대상 dataset의 분포를 파랑/주황/초록 3개의 정규 분포의 결합이라고 가정
2. 각 데이터 포인트가 각 정규 분포에 속할 확률을 계산 후, 가장 큰 확률을 갖는 정규 분포로 할당

3. 각 정규 분포 그룹의 데이터 포인트를 사용해, MLE로 모분산, 모평균을 추정
4. 정규 분포의 평균, 분산이 변하지 않을 때까지 1~3을 반복

장점과 단점

장점

1. 유연한 클러스터 형태: 각 클러스터가 가우시안 분포로 모델링되므로, 타원형 클러스터와 같은 다양한 형태를 표현할 수 있음
2. 소프트 클러스터링: 각 데이터 포인트가 여러 클러스터에 속할 확률을 가지므로, 데이터 포인트가 여러 클러스터에 걸쳐 있는 경우 유연하게 처리할 수 있음
3. 확률 모델링: 데이터의 생성 과정을 확률적으로 모델링하여, 밀도 추정과 같은 작업에 유용

단점

1. 복잡성: EM 알고리즘은 계산 비용이 높으며, 수렴 속도가 느릴 수 있음
2. 초기화 민감성: 초기 매개변수 설정에 따라 결과가 크게 달라질 수 있다. 적절한 초기값을 선택하지 않으면, local minima에 빠질 수 있음
3. 가우시안 분포 가정: 각 클러스터가 가우시안 분포를 따른다고 가정하므로, 실제 데이터 분포가 이 가정을 따르지 않는 경우 성능이 저하될 수 있음

Agglomerative Hierarchical Clustering

• 계층적 클러스터링 방법 중 하나로, 데이터를 클러스터로 그룹화하는 과정에서 점진적으로 클러스터를 병합해 나가는 bottom-up 접근 방식
• 데이터 포인트를 개별 클러스터로 시작하여, 가장 가까운 클러스터 쌍을 반복적으로 병합해가면서 클러스터의 계층적 구조를 형성

알고리즘 단계

1. 초기화: 각 데이터 포인트를 하나의 클러스터로 간주. 초기 상태에서는 $n$개의 데이터 포인트가 $n$개의 클러스터를 형성

2. 거리 계산:
   • 클러스터 간의 거리(또는 유사도)를 계산
     • 최단 거리 (Single Linkage): 두 클러스터 간 가장 가까운 데이터 포인트 간의 거리.
     • 최장 거리 (Complete Linkage): 두 클러스터 간 가장 먼 데이터 포인트 간의 거리.
     • 평균 거리 (Average Linkage): 두 클러스터 간 모든 데이터 포인트 간의 평균 거리.
     • 중심 거리 (Centroid Linkage): 두 클러스터의 중심(평균) 간의 거리.
3. 클러스터 병합: 가장 가까운 두 클러스터를 병합. 병합 후, 클러스터의 수가 하나 줄어든다
4. 반복: 위의 단계 2와 3을 클러스터의 수가 하나가 될 때까지 반복

5. 덴드로그램(Dendrogram) 생성: 계층적 클러스터링 과정을 시각화한 트리 형태의 구조. 덴드로그램을 통해 클러스터의 병합 과정을 시각적으로 확인할 수 있으며, 클러스터의 수를 결정할 숭 있음

장점과 단점

장점

1. 유연성: 클러스터의 수를 사전에 지정할 필요가 없으며, 덴드로그램을 통해 적절한 클러스터의 수를 선택할 수 있음
2. 다양한 형태의 클러스터 탐지 가능: 클러스터 간의 거리를 측정하는 다양한 방법을 사용할 수 있어, 다양한 형태와 크기의 클러스터를 탐지할 수 있음
3. 시각적 이해 용이: 덴드로그램을 통해 클러스터링 과정을 직관적으로 이해할 수 있음

단점

1. 계산 복잡성: 큰 데이터셋에서는 계산 비용이 매우 높음. 초기 상태에서 $n$개의 클러스터가 있으므로, 클러스터 병합 과정을 반복할 때마다 거리 계산이 필요
2. 병합 후 수정 불가: 한 번 병합된 클러스터는 다시 분할할 수 없음. 초기 단계에서 잘못된 병합이 이루어지면, 최종 결과에 영향을 미칠 수 있음
3. 노이즈와 이상치에 민감: 이상치나 노이즈 데이터 포인트가 클러스터 병합 과정에 큰 영향을 미칠 수 있음

Clustering Metric

Silhouette Coefficient, Davies-Bouldin Index, Within-cluster Sum of Squares(WCSS), Compactness 등

실제 label이 존재할 경우 Accuracy, F1 score, NM1, ARI 등도 사용 가능

Silhouette Coefficient

• 데이터 포인트가 얼마나 잘 클러스터링되었는지를 평가하는 지표로, 클러스터 내 응집력과 클러스터 간 분리도를 기반으로 계산
• 값이 1에 가까울수록 클러스터링 품질이 높고, -1에 가까울수록 클러스터링 품질이 낮음

1. 내부 클러스터 거리 $a(i)$:

   • 데이터 포인트 $i$와 같은 클러스터 내에 있는 다른 모든 데이터 포인트 간의 평균 거리입니다.
   • $a(i) = \frac{1}{|C_i| - 1} \sum_{j \in C_i, j \neq i} d(i, j)$
   • 여기서 $C_i$는 데이터 포인트 $i$가 속한 클러스터이며, $d(i, j)$는 데이터 포인트 $i$와 $j$ 간의 거리

2. 최소 외부 클러스터 거리 $b(i)$:

   • 데이터 포인트 $i$와 가장 가까운 다른 클러스터의 모든 데이터 포인트 간의 평균 거리
   • $b(i) = \min_{C_k \neq C_i} \frac{1}{|C_k|} \sum_{j \in C_k} d(i, j)$
   • 여기서 $C_k$는 데이터 포인트 $i$가 속하지 않은 클러스터

3. 실루엣 계수 $s(i)$:

   • 실루엣 계수는 $a(i)$와 $b(i)$를 사용하여 다음과 같이 계산:
   • $s(i) = \frac{b(i) - a(i)}{\max(a(i), b(i))}$
   • 실루엣 계수 $s(i)$의 값은 -1에서 1 사이:
     • $s(i) \approx 1$: 데이터 포인트 $i$가 잘 클러스터링되어 있음.
     • $s(i) \approx 0$: 데이터 포인트 $i$가 클러스터 경계에 위치해 있음.
     • $s(i) \approx -1$: 데이터 포인트 $i$가 잘못 클러스터링되어 있음.

• 전체 데이터셋에 대한 실루엣 계수는 각 데이터 포인트의 실루엣 계수의 평균으로 계산:
  • $s = \frac{1}{N} \sum_{i=1}^{N} s(i)$
  • 여기서 $N$은 데이터셋 내의 총 데이터 포인트 수

---

Further Study

• Dimension reduction

---

참고

• 데이터 사이언티스트가 알고 있어야 할 5 가지 클러스터링 알고리즘
• [ML] 군집화 - Mean Shift Clustering
• Kernel Density Estimation(커널밀도추정)에 대한 이해
• [머신러닝/ML] 군집화 (Clustering)
• [머신러닝] GMM(Gaussian Mixture Model) 군집화