[Paper Review] Learning Graph Neural Networks with Positive and Unlabeled Nodes

Hanseok Jo·2021년 5월 25일

Paper Review

목록 보기

2/5

이번에 리뷰할 논문은 Learning Graph Neural Networks with Positive and Unlabeled Nodes 으로 CIKM 19'에 short version으로 나온 Long-short Distance Aggregation Networks for Positive Unlabeled Graph Learning의 full version이다. ~~arxiv에 올라온거라 그런지 중간중간 typo는 좀 보임~~

Wu, Man, et al. "Learning Graph Neural Networks with Positive and Unlabeled Nodes." arXiv preprint arXiv:2103.04683 (2021).

Wu, Man, et al. "Long-short Distance Aggregation Networks for Positive Unlabeled Graph Learning." Proceedings of the 28th ACM International Conference on Information and Knowledge Management. 2019.

TR;DL🙃

adjacency matrix $A^k$ 만을 이용한 short distance attention과 이를 활용하여 input과 결합한 long distance attention을 제안하고, 이 방식이 좋은 성능을 보인다는걸 실험적으로 증명함

PU graph learning 을 위해 기존의 PU learning에서 사용되던 unbiased risk estimator와 non-negative risk estimator를 제안하고, 이 방식 역시 좋은 성능을 보인다는걸 실험적으로 증명함

1 INTRODUCTION

node content information과 graph structure를 low dimension으로 매핑하는 representation learning은 크게 2가지 방식이 있음.

two-step graph embedding based classificaiton algorithms
- two step이라서 learned node features가 classification을 위한 best representation이 아닐 수 있음
end-to-end graph convoluctional neural nets methods

1.1 Motivation

Limitations of GNN
- GAT와 같은 GNN은 1-hop neighbor node만 고려하기 때문에 long distance relationship은 무시됨
- classification을 위해선 2개 이상의 label이 필요함
  - 하지만 real world에선 single label의 데이터만 있는 경우도 존재함
  위와 같은 limitation으로 인해 PU learning을 위해 long-short distance relationship을 고려한 GNN을 제안함

1.2 Challenges and Contibution

Chanllenges

long-distance neighbor의 정보를 어떻게 반영할 것인가?
PU graph learning을 어떻게 design 할 것인가?

Long-short distance aggregation network(LSDAN)

n-hop neighbor별로 adjacency matrix를 만들고 attention mechanism을 이용하여 node importance (인접 node 및 거리별 node 모두 고려함)
새로운 risk estimators를 적용함

Contributions

network에 GNN을 이용한 PU learning을 처음 제안함
short distance와 long distance의 node significance를 반영할 수 있는 attention network를 제안함
benchmark graph datasets에서 baseline methods보다 자기네들이 제안한 모델의 성능이 더 좋음

2.1 Graph Neural Networks

(생략함)

2.2 Positive Unlabeled Learning

현재 PU methods는 unlabeled data(U)를 어떻게 처리하느냐 따라 두 방식으로 나눌 수 있음

two-step strategy: U에서 possible negative(N)를 찾아내고 일반적인 supervised learnig을 수행함 -> heuristic하게 N을 찾는다는 단점 존재
direct learning method: U을 small weight N으로 가정하고 One-class SVM, Biased-SVM 같은 classification을 수행함 -> weight에 따라 결과가 달라지는데 computational cost가 커서 튜닝하기 힘듬

위의 이슈를 해결하기 위한 몇몇 unbiased PU learning methods가 있었음

Niu and Sugiyama1's work: intrinsic bias를 피하기 위한 unbiased risk estimator를 제안
overfitting에 robust한 non-negative risk estimator2
하지만 1, 2는 non-graph / non-relational data에 적용하였음

2.3 PU Learning for Graph Data

이 논문이 기존의 graph data에서 PU learning을 해결하는 연구와 다른점은

기존 연구는 inductive graph learning이지만 이 논문은 transductive graph learning임
기존 연구는 shallow and biased이지만 이 논문은 unbiased and deep neural net임
이 논문은 graph feature learning과 classification task를 end-to-end로 해결함

3 PROBLEM STATEMENT

Table 1. Summary of Notations and Symbols

Positive Unlabeled Graph Learning(PUGL)
Given a graph $G=(V,E,X,Y)$ , Positive Unlabeled Graph Learning aims to learn a binary classification model, $f: (A, X;P) \mapsto Y$ , to predict the class labels for unlabeled nodes $U$

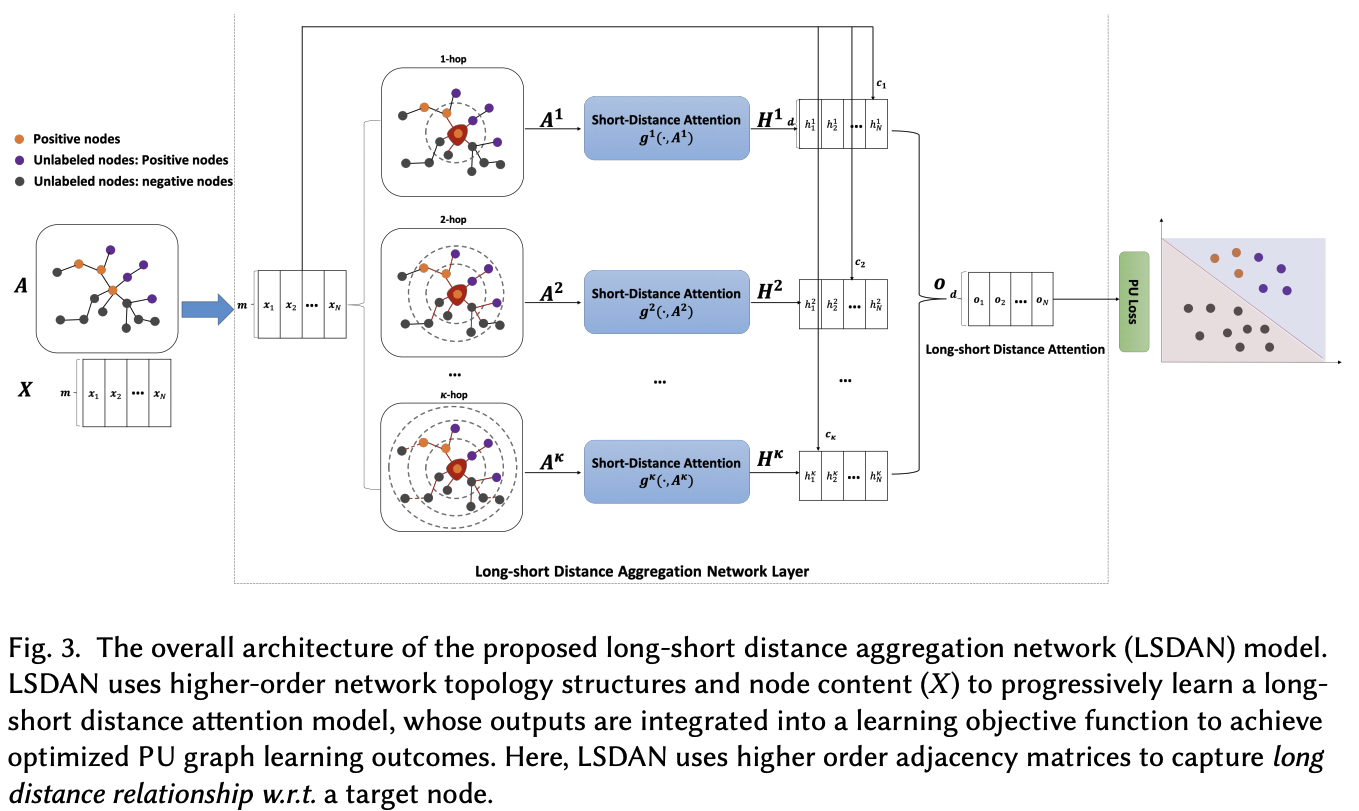
4 LONG-SHORT DISTANCE AGGREGATION NETWORKS FOR PU GRAPH LEARNING

Three components of LSDAN

Short-Distance Attention
Long-short Distance Attention
Positive Unlabeled Learning

4.1 Short-Distance vs. Long-Distance

SHORT-DISTANCE is defined as the distance from direct (1-hop) neighbor nodes to a target node.
LONG-DISTANCE is defined as the distances of k-hop neighbors (k>1) to a target node. The (normalized) adjacency matrix A의 multiple matrix multiplication ( $A^k$ )를 통해 나타낼 수 있음.

4.2 Long-short Distance Attention

4.2.1 Short-Distance Attention

Embedding features of each node is defined as

h_i = g \left (\sum_{j} \alpha_{i, j}A_{i, j}W^{(1)} \mathbf{x}_j \right)

where $g$ is a non-linear activation function.

To compute attention weight $\alpha_{i, j}$ , an attention coefficient $t_{i, j}$ is computed by an attention function $a_{tt}\left(\cdot \right)$ :

t_{i, j} = a_{tt} \left (W^{(1)}\mathbf{x}_i, W^{(1)}\mathbf{x}_j \right)

And an attention coefficient is normalized using softmax function:

\alpha_{i, j} = softmax_j \left (t_{i, j} \right) = {{\mathit{exp} \left (t_{i, j} \right)} \over {\sum_J A_{i,J} \mathit{exp} \left(t_{i, J}\right)}}

4.2.2 Long-Distance Attention

전반적으로 (당연하지만) 4.2.1과 유사함
k-hop neighbor을 나타내긴 위해 matrix $B^k$ 를 다음과 같이 정의

B^{k}_{i, j} = \begin{cases} 1 & \mathrm{if} \ A^k_{i, j} \neq 0 \\ 0 & \mathrm{Otherwise.} \end{cases}

그리고 k-hop neighbor를 aggregate한 feature embedding은 다음과 같이 표현할 수 있다.

h_i^{k} = g \left (\sum_{j} \alpha_{i, j}B^k_{i, j}W^{(1)} \mathbf{x}_j \right)

그리고 long-distance attention weight $c^k_i$ 는 다른 attention mechanism과 같이 다음과 같이 계산할 수 있다.

c^k_i = {\frac{\mathit{exp}\left(a_{ls}\left(h^k_i, W^{(2)} \mathbf{x}_j\right)\right)}{\sum_{k=1}^K \mathit{exp}\left(a_{ls}\left(h^k_i, W^{(2)} \mathbf{x}_j\right)\right)}}

여기서 $a_{ls}$ 는 dot-product attention function을 의미한다.

앞의 모든 과정을 종합해서 만든 embedding output $\mathrm{O} \in \mathbb{R}^{(n \times d)}=\left\{\mathrm{o_1}, \cdot\cdot\cdot,\mathrm{o_n} \right\}$ 은 다음과 같다.

\mathrm{o_i} = \sum_{k=1}^\kappa{c_i^k}{h_i^k}

4.3 Deep Long-short Distance Aggregation Networks

4.2에서 만든 component를 하나의 submodule(논문에서는 Long-Short Distance Aggregation Network Layer라고 표현)로 두고 얘를 L개를 쌓아서 deep한 구조를 만든다. 이 때 residual connection을 Fig. 6.과 같이 사용함.
마지막의 $\mathrm{O}^L$ 은 PU classification을 위해 2-dim으로 만든다.

사족🐍: 이 논문에서 제안하는 network 구조 대신 일반적인 GNN architecture를 사용했어도 PU learning은 가능했을 것 같은데..
사족🐍2: 뒤에 실험결과로 이 논문에서 제안하는 network 구조가 GCN, GAT보다 좋다는걸 보여줍니다.

4.4 Positive and Unlabeled Graph Learning

4.4.1 Traditioanl Binary Classification

Notations

a model $\mathit{f} : \mathcal{O} \to \mathcal{Y}$ and the ground-truth label of node $\mathcal{Y}=\left\{+1, 0\right\}$
loss function: $\mathcal{L}\left(y^\prime, y\right)$
class-prior probability $\pi_{p}=p(Y=+1)$ and $\pi_{n}=p(Y=0)=1-\pi_{p}$

Traditional binary classification problem i.e., positive and negative learning (PN learning), we can minimize an approximated $R\left(f\right)$ by,

\hat{R}_{pn}(f) = \pi_{p}\hat{R}^{+}_{p}(f) + \pi_{n}\hat{R}^{-}_{n}(f)

where $\hat{R}^{+}_{p}(f)=\left(1 / {n_p} \right) \sum^{n_p}_{i=1}\mathcal{L}\left(f\left(\mathrm{o}^p_i, +1\right)\right)$ and $\hat{R}^{-}_{n}(f)=\left(1 / {n_p} \right) \sum^{n_n}_{i=1}\mathcal{L}\left(f\left(\mathrm{o}^n_i, 0\right)\right)$ . Here, $n_p$ and $n_n$ denote the number of positive/negative samples, respectively.

4.4.2 Unbiased Risk Estimator for PU Learning

PU learning에서는 $\pi_{n}\hat{R}^{-}_{n}(f)$ 를 계산할 수 없기 때문에 approximate해서 사용해야 한다.
3에서 제안한 unbiased risk estimator를 이용하여 다음과 같이 표현할 수 있다.

\pi_{n}\hat{R}^{-}_{n}(f) = -\pi_{p}\hat{R}^{-}_{p}(f) + \hat{R}^{-}_{u}(f)

where $\hat{R}^{-}_{p}(f)=\left(1 / {n_p} \right) \sum^{n_p}_{i=1}\mathcal{L}\left(f\left(\mathrm{o}^p_i, 0\right)\right)$ and $\hat{R}^{-}_{u}(f)=\left(1 / {n_u} \right) \sum^{n_u}_{i=1}\mathcal{L}\left(f\left(\mathrm{o}^u_i, 0\right)\right)$ . Here, $n_p$ and $n_u$ denote the number of positive/unlabeled samples, respectively.

따라서 PU learning에서의 risk $R(f)$ 는

\hat{R}_{pu}(f) = \pi_{p}\hat{R}^{+}_{p}(f) -\pi_{p}\hat{R}^{-}_{p}(f) + \hat{R}^{-}_{u}(f)

4.4.3 Non-negative Risk Estimator for PU Learning

위에서 언급한 risk $R(f)$ 에 minus term이 있어서 loss가 0이 되어 overfitting이 생길 수 있는 위험성이 있음. 2에서 제안한 non-negative risk estimator를 적용해서 최종적으로 다음과 같은 같은 $R(f)$ 를 얻을 수 있다.

\hat{R}_{pu}(f) = \pi_{p}\hat{R}^{+}_{p}(f) + \mathrm{max} \left\{0, -\pi_{p}\hat{R}^{-}_{p}(f) + \hat{R}^{-}_{u}(f) \right\}

이 논문에서는 mapping function $f$ 를 sigmoid로, loss function $\mathcal{L}\left(y^\prime, y\right)$ 은 cross-entropy를 사용하였음.

4.5 Algorithm Description

4.6 Time Complexity Analysis

real world에서는 time complexity를 $O(\kappa \left|V \right|^3)$ 로 간주해도 무방함.

5 EXPERIMENTS

5.1 Experiment Setting

Datasets

Cora, Citeseer, DBLP dataset 사용
Multilabel dataset이라서 상대적으로 많은 수를 가진 class를 positive, 나머지를 negative로 두고 binary classification 문제로 변환

Baselines

Classifical PU learning method (one-step strategy and two-step strategy)
- OC-SVM: OC means One-class SVM
- LINE_OC-SVM
- GAE_OC-SVM: GAE means Graph Auth-Encoder
- Roc-SVM: Roc means Rocchio method
- LINE_ROC-SVM
- GAE_ROC-SVM
DL model with unbiased risk estimator and non-negative risk estimator
- FC: fully connected network
- FS: fully connected self-attention network
- GCN: graph convolutional network
- GAT: graph attention nets
- GATH: graph attention nets with multi-head attention
LSDAN
- LSDAN_UPU: LSDAN with unbiased risk estimator
- LSDAN_NNPU: LSDAN with non-negative risk estimator

Experimental Setup
positive class data 중 일부를 랜덤 샘플링(%p만큼)하여 training set으로 두고 나머지 positive class data와 모든 negative class data를 unlabeled set으로 사용. 10 trials 후 average F1 Score를 지표로 성능 평가

5.2 Experimental Results

실험결과 해석중 중요한 부분만 요약해보겠습니다.

One-class SVM과 Roc-SVM은 별로다.
GAE를 이용한 two-step strategy가 one-step이나 LINE을 이용한 two-step strategy보다 좋다.
FC, FS보단 GAT가, GAT보단 GATH가 좋다.
그리고 LSDAN이 더 좋다.
UPU랑 NNPU를 같이 쓰는게 좋다.

뭐.. 당연히 자기네들이 제안한게 좋다는 내용입니다. 자세한 수치는 아래 첨부한 표를 통해 확인 바랍니다.

Experimental result tables

5.3 Analysis of Different Components

이 논문은 long-short distance aggregation, PU loss가 contribution인만큼 이 2개의 component 유무에 따른 성능도 비교하였습니다. 뭐.. 물론 쓴게 더 좋겠죠. 자세한 수치는 아래 첨부한 표를 통해 확인바랍니다. ( $\lnot p$ 는 PU loss를 제거한 모델, $\lnot l$ 은 long-short distance aggregation layer를 제거한 모델을 의미합니다.)

Analysis of different components tables

5.4 Analysis of Learned Long-Distance Attention

Long-Distance Attention mechanism을 쓰면 왜 좋은지 분석했습니다. $A^k$ 만 사용했을 때의 attention weight와 F1 score를 비교했는데, 두 값이 양의 상관관계가 있음을 실험적으로 알아냈습니다. 즉, long distance node의 정보를 잘 반영할수록 성능이 좋아진다는 것을 의미합니다..? (맞나?) 자세한 실험 결과는 아래 그래프를 참고해주시기 바랍니다.

Analysis of learned long-distance attention figures

5.5 Parameter Analysis

Embedding Dimensions: embedding dimension이 커질수록 더 많은 정보를 encode 할 수 있다고 대략 결론내릴 수 있음
Distance at $\kappa$ -Hops: long distance relationship이 중요하긴 하지만 너무 long 하면 오히려 학습에 방해됨을 알 수 있음
Number of layers: layer를 늘릴수록 성능이 좋아졌다가 나빠진 후 다시 좋아지는데, 좋아졌다가 나빠지는건 layer를 너무 많이 쌓는게 학습에 방해된다는 뜻이고 나빠졌다가 다시 좋아지는건 overfitting을 의미함
자세한 실험 결과는 아래 그래프를 참고해주시기 바랍니다.

Parameter Analysis figures

6 DISCUSSION

위에서 했던 얘기의 요약의 요약입니다. 특별한 내용은 없어요.

7 CONCLUSION

결국, 자기들이 제안한 모델이 좋다는 얘기입니다.

References in post

Gang Niu and Masashi Sugiyama. 2015. Convex formulation for learning from positive and unlabeled data. In Proc. of ICML. 1386–1394
Ryuichi Kiryo, Gang Niu, Marthinus C. Du Plessis, and Masashi Sugiyama. 2017. Positive-Unlabeled Learning with Non-Negative Risk Estimator. In Proc. of NIPS. 1674–1684.
M. C. Du Plessis, Gang Niu, and Masashi Sugiyama. 2014. Analysis of Learning from Positive and Unlabeled Data. In Proc. of NIPS. 703–711

Hanseok Jo

AITRICS에서 ML, CS, Statistics를 이용해서 Drug discovery를 하고 있습니다.

이전 포스트

[Paper Review] Inferring Novel Tumor Suppressor Genes with a Protein-Protein Interaction Network and Network Diffusion Algorithms

다음 포스트