Kalman Filter(칼만필터)

이준혁·2025년 11월 13일
control systemmobility_enginering

control_system

목록 보기
2/4

칼만필터

칼만 필터는 “수학적 모델(예측)”과 “센서 측정값(보정)”을 최적으로 결합하여
잡음이 있는 환경에서도 가장 신뢰할 수 있는 상태 추정값을 제공하는 알고리즘


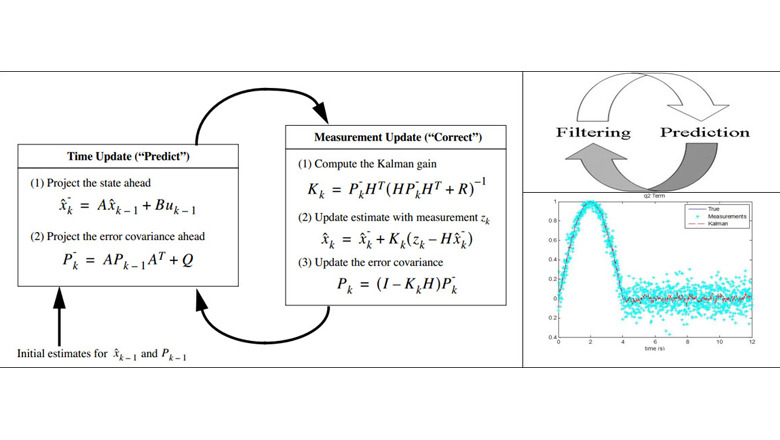
해당 수식이 칼만필터의 개념임
(각 알파벳위에 '-'가 있다면 추정값이라고 생각하면 됨)

이를 쉽게 나태내면

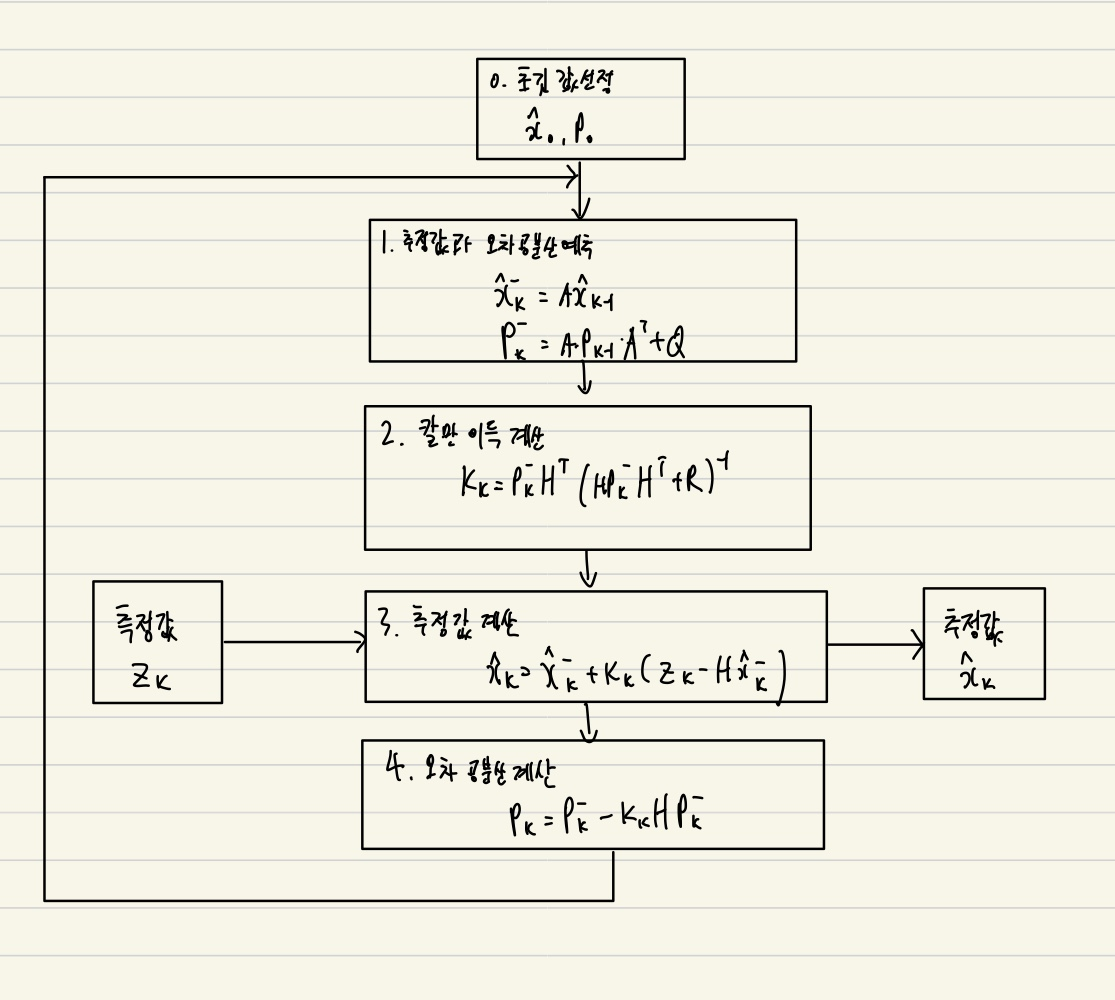
칼만 필터의 순서 설명

1. 초기값 설정

  • x0x^{0} : 처음 상태에 대한 '추정값'
  • P0P_{0} : 이 추정값이 얼마나 불확신한지 알려주는 오차 공분산
  • 오차 공분산이란 추정한 값이 실제 값으로부터 얼마나 불확실하게 퍼져있는지를 수핮거으로 표현한 것

해당 단계에서는 처음에 시스템 상태를 어떻게 알고 있다고 가정할지를 정하는 단계

2. 추정값과 오차 공분산 예측단계

x^k−=Ax^k−1\hat{x}_{k}^{-} = A \hat{x}_{k-1}

2-1 상태 예측하는 부분

  • A : 시스템 모델로 상태 전이행렬 (이전 상태에서 다음 상태로 변환하는 것)
  • x^k−1\hat{x}_{k-1} : 예측된 상태 값
Pk−=APk−1AT+QP_{k}^{-} = A P_{k-1} A^{T} + Q

2-2 오차 공분산 예측

  • Pk−P_{k}^{-} : 에측 단계에서 상태의 불확실성이 얼마나 커졌는지 확인
  • Q : 프로세스 노이즈로 모델의 불완전성을 나타냄

이 부분에서 Q의 증가량이 볼확실성을 의미함

3. 칼만 이득 계산(Gain)

Kk=Pk−HT(HPk−HT+R)−1K_{k} = P_{k}^{-} H^{T} ( H P_{k}^{-} H^{T} + R )^{-1}
  • H : 상태를 측정 공간으로 변환하는 행렬
  • R : 센서 노이즈의 공분산을 뜻함
  • KkK_{k} : 센서를 얼마나 믿을지 결정하는 가중치
    -> 이를 간단하게 이야기하면 R(센서 노이즈)가 크면 센서를 덜 믿고 P(예측 오차)가 크면 센서를 더 믿음

4. 추정값 계산

x^k=x^k−+Kk(zk−Hx^k−)\hat{x}_{k} = \hat{x}_{k}^{-} + K_{k}( z_{k} - H\hat{x}_{k}^{-} )

4-1 innovation

  • 센서가 측정한 값 : zkz_{k}
  • 예측한 값 : Hx^k−H\hat{x}_{k}^{-}
  • 둘의 차이를 오차를 구함
    -> 이는 예측한 값과 실제 센서 측정값과의 차이가 얼마나 다른지 판단

4-2 추정값 업데이트

  • x^k−\hat{x}_{k}^{-}인 예측 값에 더해주면서 새 추정값을 얻음 이는 센서와 예측을 섞어

5. 오차 공분산 계산

Pk=(I−KkH) Pk−P_{k} = (I - K_{k}H)\, P_{k}^{-}
  • 이부분에서는 업데이트 이후 상태 추정의 불확실성이 얼마나 줄었는지를 계산함
  • K와 H가 포함된 이유는 센서를 얼마나 반영했는지 확인해야 하기 때문
  • 센서 정보를 반영한 뒤 우리가의 불확실성이 어느 정도로 줄었는지 계산함
  • 항등행렬에서 빼서 진행함

해당 그림처럼 되는데 해당 부분에서 구해야 하는 부분은
A,Q,H,R을 구하는 것이 최종 목표임 이를 구하면 나머지 값들은 계산을 통해 구할수 있음
Q,R은 여기서 노이즈의 형태로 데이터가 주어지는 경우가 많다
그래서 A와 H를 먼저 본다

상태공간방정식

해당 개념을 이해하려면 상태공간 방정식의 개념이 필요함

상태 방정식

-> A 구함

-> 상태 전이 행렬

관측 방정식

-> H 구함

Q와 R

R : 센서 측정 노이즈 공분산

센서는 항상 노이즈가 있으며, 이를 수식에 반영한 것이 R입니다.

zk=Hxk+vk,vk∼N(0,R)z_k = Hx_k + v_k,\qquad v_k \sim \mathcal{N}(0, R)
  • Vk : 측정 노이즈
  • Vk ~ N(0,R) : 평균 0, 공분산 R을 가지는 가우시안 노이즈
  • Rdms 센서의 노이즈 크기를 나태내는 행렬
  • 센서가 불안정할수록 R은 커짐

Q : 시스템(모델) 노이즈 공분산

모델이 아무리 정확해도 현실을 100% 표현할 수 없기 때문에
모델링 오차를 Q로 반영합니다.

xk+1=Axk+wk,wk∼N(0,Q)x_{k+1} = A x_k + w_k,\qquad w_k \sim \mathcal{N}(0, Q)
  • wk : 모델리 ㅇ 오차, 외란
  • 모델 불확실성이 크면 Q를 크게 설정함

R과 Q는 Gaussian(정규분포)의 형태를 만듬

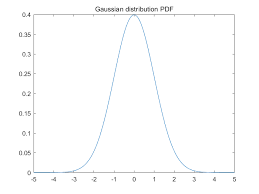
  • 대부분의 통신, 전자공학, 센서들의 노이즈가 가우시안 형태임
    -> 열 잡음, 미세 진동, 측정 오차
    이들은 가우시안 분포를 만듬

P(오차공분산)

Pk−=APk−1AT+QP_{k}^{-} = A P_{k-1} A^{T} + Q
  • 추정값과 실제값의 차이를 가우시안 분포를 그릴때의 분산값이라 함
  • 해당것은 수식을 대입하여 계산하면됨

K(칼만이득)

Kk=Pk−HT(HPk−HT+R)−1K_{k} = P_{k}^{-} H^{T} ( H P_{k}^{-} H^{T} + R )^{-1}
  • R은 sensor의 Noise로 R이 증가하면 K는감소하게 되는 구조
  • 식을 대입하면 계산 가능
R에 대해서
x^k=x^k−+Kk(zk−Hx^k−)\hat{x}_{k} = \hat{x}_{k}^{-} + K_k (z_k - H\hat{x}_k^{-})
  • 단일 변수 시스템에서 H=1H = 1로 상수취급하변 수식은 단순화됩니다.
x^k=(1−Kk)x^k−+Kkzk\hat{x}_{k} = (1 - K_k)\hat{x}_k^{-} + K_k z_k
  • 이는 Low pass filter의 모양이 나오게 됨
  • zkz_k는 센서로 측정한 값으로 k 값이 작아지면 센서의 값을 덜보고 이전에 추정한 weighting을 많이 준다는 뜻
  • R(센서 노이즈가)가 크면 k가 줄어듬 이로인해 최종 추정값에서 센서에 대한 비중 축소
Q에 대해서

  • Q는 시스템 모델이 현실을 완벽하게 표현하지 못해 발생하는 프로세스 노이즈

  • 상태 예측 공분산은 다음과 같음

Pk−=APk−1AT+QP_k^{-} = A P_{k-1} A^{T} + Q
  • 여기서 Q가 증가하면 예측 공분산 Pk−P_k^{-} 가 증가함
Kk=Pk−HT(HPk−HT+R)−1K_k = P_k^{-} H^{T} (H P_k^{-} H^{T} + R)^{-1}

  • 해당 kalman gain의 공식을 보면 예측 공분산 Pk−P_k^{-} 가 커지면 분자와 분모 중 분자가 더 큰 비율로 증가하여 최종적으로 Kalman Gain KkK_k 가 증가합니다.

  • Q(시스템의 모델의 불확실성)이 크다는 것은 모델 예측을 신뢰하기가 어렵다는 의미

  • 이를 통해 알수 있는것은 Q가 증가하면 Pk−P_k^{-}가 증가하여 kalman gain도 증가하며 센서값의 영향력이 증가 하는것을 확인

    참조

https://limitsinx.tistory.com/72#google_vignette

칼만필터는 어렵지않아 (2019,김성필)

profile
이준혁
#자기공부 #틀린것도많음 #자기개발 여러분 인생이 힘들다 하더라도 그것을 깨는 순간 큰 희열감으로 옵니다~
이전 포스트

PID SIMULINK

다음 포스트

Extended Kalman Filter(확장칼만필터)

0개의 댓글