Extended Kalman Filter(확장칼만필터)

이준혁·2025년 11월 17일
control systemmobility_enginering

control_system

목록 보기
3/4
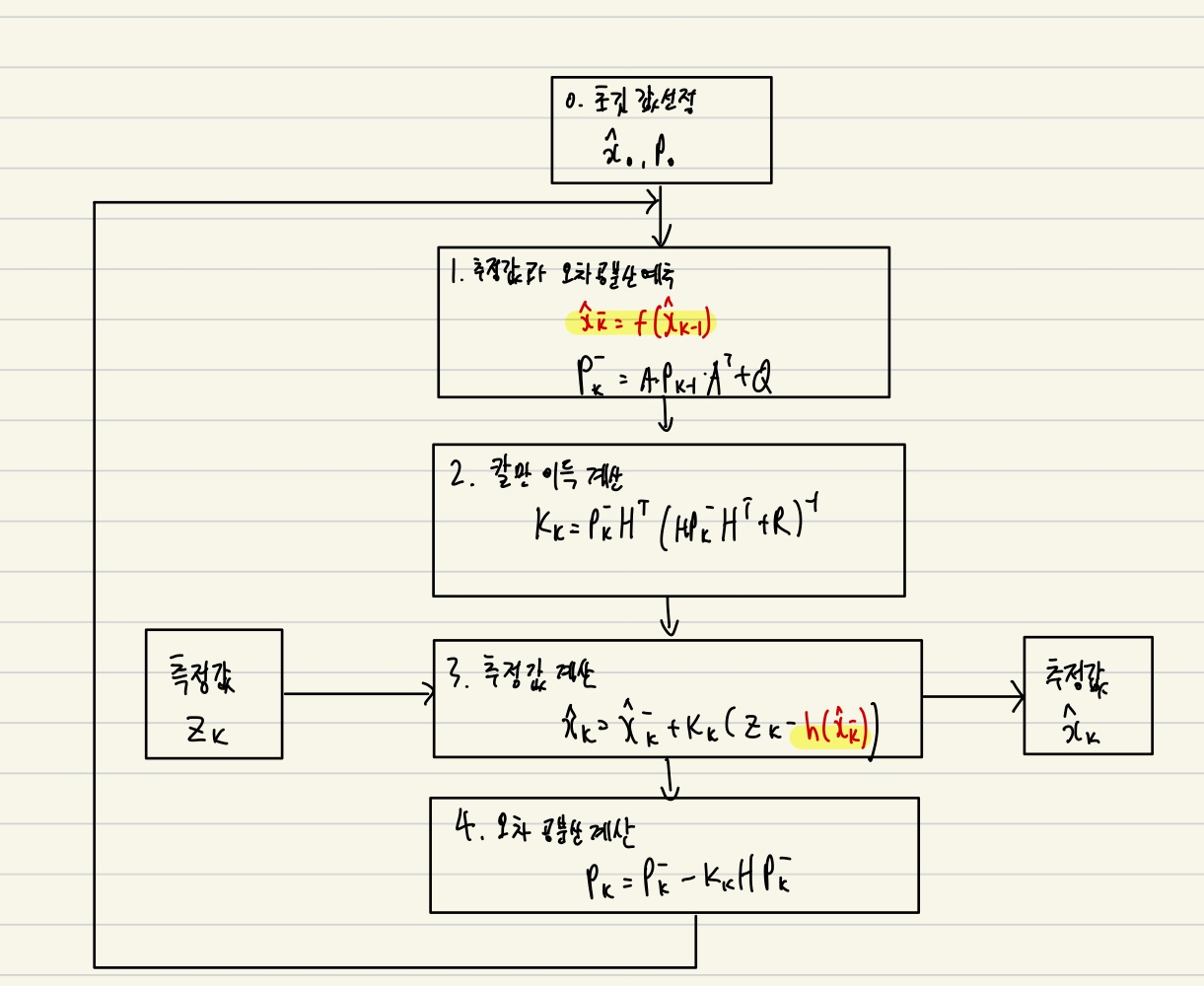
post-thumbnail

확장 칼만필터(Extended Kalman Filter)

칼만 필터는 선형식일때 사용하면 되는 것이고 확장칼만필터는 비선형함수가 있는경우 이를 해결하기 위해 미분해서 선형으로 만들어서 사용하는 것

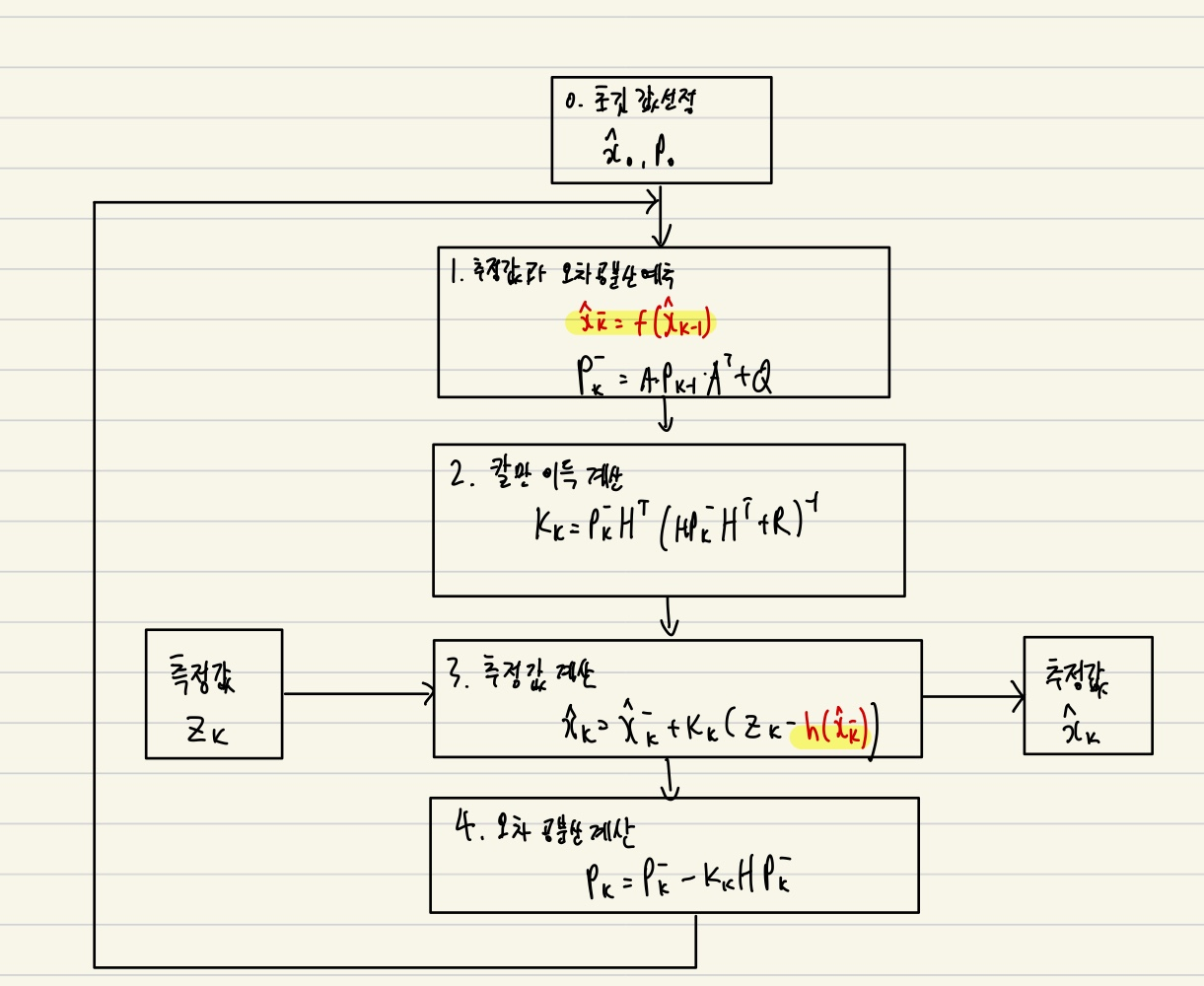
  • 해당 부분에서 선형과 다른 부분은 빨간색 부분만이 다른 부분임
  • 이부분이 비선형이 추가된것임

확장 칼만필터의 순서 설명

1. 초기값 설정

  • x0x^{0} : 처음 상태에 대한 '추정값'
  • P0P_{0} : 이 추정값이 얼마나 불확신한지 알려주는 오차 공분산
  • 오차 공분산이란 추정한 값이 실제 값으로부터 얼마나 불확실하게 퍼져있는지를 수핮거으로 표현한 것

해당 단계에서는 처음에 시스템 상태를 어떻게 알고 있다고 가정할지를 정하는 단계

2. 추정값과 오차 공분산 예측단계

x^k∣k−1=f(x^k−1)\hat{x}_{k|k-1} = f(\hat{x}_{k-1})

2-1 상태 예측하는 부분

  • 이전 상태를 기반으로 시스템 모델을 f(.)을 적용하여 다음 상태를 예측
Pk−=APk−1AT+QP_{k}^{-} = A P_{k-1} A^{T} + Q

2-2 오차 공분산 예측

  • Pk−P_{k}^{-} : 에측 단계에서 상태의 불확실성이 얼마나 커졌는지 확인
  • Q : 프로세스 노이즈로 모델의 불완전성을 나타냄

이 부분에서 Q의 증가량이 볼확실성을 의미함

3. 칼만 이득 계산(Gain)

Kk=Pk−HT(HPk−HT+R)−1K_{k} = P_{k}^{-} H^{T} ( H P_{k}^{-} H^{T} + R )^{-1}
  • H : 상태를 측정 공간으로 변환하는 행렬
  • R : 센서 노이즈의 공분산을 뜻함
  • KkK_{k} : 센서를 얼마나 믿을지 결정하는 가중치
    -> 이를 간단하게 이야기하면 R(센서 노이즈)가 크면 센서를 덜 믿고 P(예측 오차)가 크면 센서를 더 믿음

4. 추정값 계산

x^k=x^k+Kk (zk−h(x^k))\hat{x}_{k} = \hat{x}_{k} + K_{k}\,\bigl( z_{k} - h(\hat{x}_{k}) \bigr)

4-1 innovation

  • 센서가 측정한 값 : zkz_{k}
  • 예측한 값 : h(x^kh(\hat{x}_{k}
  • 둘의 차이를 오차를 구함
    -> 이는 예측한 값과 실제 센서 측정값과의 차이가 얼마나 다른지 판단

4-2 추정값 업데이트

  • x^k−\hat{x}_{k}^{-}인 예측 값에 더해주면서 새 추정값을 얻음 이는 센서와 예측을 섞어

5. 오차 공분산 계산

Pk=(I−KkH) Pk−P_{k} = (I - K_{k}H)\, P_{k}^{-}
  • 이부분에서는 업데이트 이후 상태 추정의 불확실성이 얼마나 줄었는지를 계산함
  • K와 H가 포함된 이유는 센서를 얼마나 반영했는지 확인해야 하기 때문
  • 센서 정보를 반영한 뒤 우리가의 불확실성이 어느 정도로 줄었는지 계산함
  • 항등행렬에서 빼서 진행함

비선형 부분이란

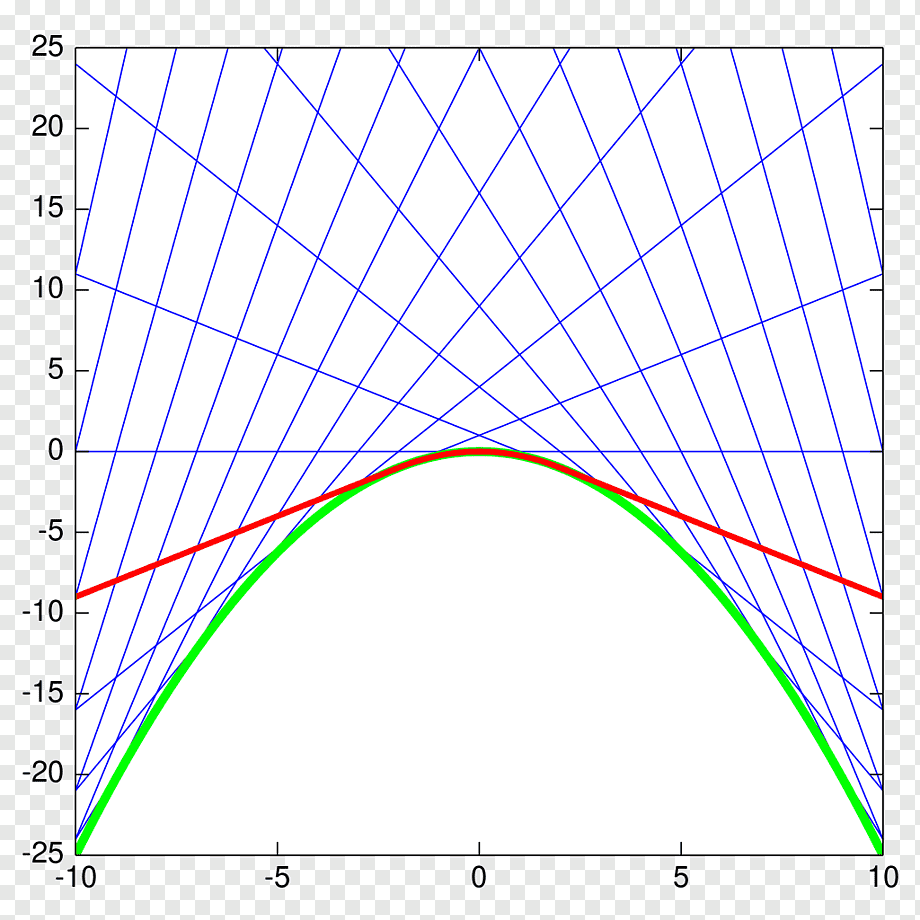
  • 저번 칼만필터에서 나온 H 부분이 h(x)로 바뀌었는데 이 부분에서 H는 상태를 측정 공간으로 변환하는 행렬로 센서와 연관있는 부분이었음
  • 이부분에서 비선형 함수를 매 순간 미분해서 선형행렬로 만들어줘 이 부분은 Jacobian을 사용해야함

Jacobian이란 편미분한다는것

  • 저번 부터 계속 언급했던 Jacobian은 선형을 비선형으로 바꾸기 위해 사용되는것으로 f(x)와 h(x)을 모든 상태 변수에 대한 편미분을 한다는것
  • 매순간 미분한다는 것은 타임 스텝마다 현재 추정된 상태에서 미분을 다시 계산하고 진행되는것

상태 벡터와 비선형 상태 모델 정의

1. 상태 벡터

x=[xyθv]x = \begin{bmatrix} x \\ y \\ \theta \\ v \end{bmatrix}

(x=위치, y=위치, θ=heading, v=속도)

2. 비선형 상태 모델

f(x)=[x+vcos⁡θ Δty+vsin⁡θ Δtθv]f(x) = \begin{bmatrix} x + v\cos\theta\,\Delta t \\ y + v\sin\theta\,\Delta t \\ \theta \\ v \end{bmatrix}
  • 해당 부분에서 x,y는 시작 좌표값이 될수있고 움직인 현재 좌표값이 될수있음
  • 우리는 지금 움직인 좌표값을 구해야하는것으로 Vcosθ△t을 구하는 것은 예를 들어 x축 만 설명을 하자면 x축의 방향 속도 성분은 V는 이동 속도 cosθ는 x값을 구하고 이에 방향을 위해 필요한것
  • 다음은 속도는는 시간단 위치 변화량이므로 Δx = v cosθ Δt로 나타나게 됨
  • 그래서 x+vcos⁡θ Δtx + v\cos\theta\,\Delta t가 되는 것임 위치 좌표 포함해서
  • 다음 속도와 방향이 필요한것

3. EKF를 위한 Jacobian

Jacobian F는 다음과 같은 4×4 구조를 가짐

F=[∂f1∂x∂f1∂y∂f1∂θ∂f1∂v∂f2∂x∂f2∂y∂f2∂θ∂f2∂v∂f3∂x∂f3∂y∂f3∂θ∂f3∂v∂f4∂x∂f4∂y∂f4∂θ∂f4∂v]F = \begin{bmatrix} \frac{\partial f_1}{\partial x} & \frac{\partial f_1}{\partial y} & \frac{\partial f_1}{\partial \theta} & \frac{\partial f_1}{\partial v} \\ \frac{\partial f_2}{\partial x} & \frac{\partial f_2}{\partial y} & \frac{\partial f_2}{\partial \theta} & \frac{\partial f_2}{\partial v} \\ \frac{\partial f_3}{\partial x} & \frac{\partial f_3}{\partial y} & \frac{\partial f_3}{\partial \theta} & \frac{\partial f_3}{\partial v} \\ \frac{\partial f_4}{\partial x} & \frac{\partial f_4}{\partial y} & \frac{\partial f_4}{\partial \theta} & \frac{\partial f_4}{\partial v} \end{bmatrix}

4. 편미분 계산 후 최종 Jacobian 행렬

F=[10−vsin⁡θ Δtcos⁡θ Δt01vcos⁡θ Δtsin⁡θ Δt00100001]F = \begin{bmatrix} 1 & 0 & -v\sin\theta\,\Delta t & \cos\theta\,\Delta t \\ 0 & 1 & v\cos\theta\,\Delta t & \sin\theta\,\Delta t \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}

결론 -> 확장 칼만 필터는 비선형화 시스템을 나타낸것으로 이렇게 편미분하여 선형근사화 시킴

참고
https://limitsinx.tistory.com/78

profile
이준혁
#자기공부 #틀린것도많음 #자기개발 여러분 인생이 힘들다 하더라도 그것을 깨는 순간 큰 희열감으로 옵니다~
이전 포스트

Kalman Filter(칼만필터)

다음 포스트

LPV 시스템

0개의 댓글