LPV 시스템

LPV 시스템은 시간에 따라 변하거나 외부 조건에 따라 변하는 파라미터를 가지지만 각 파라미터 마다 고정되어 있다고 생각하면 그 값으로 선형 시스템을 표현할수 있는 모델

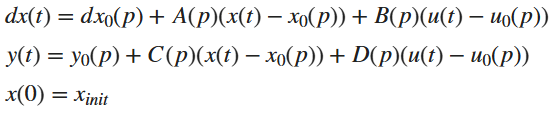
LPV 시스템은 다음과 같은 수학적으로 표현할수 있음
각각에 대한 설명을 하면

1. u(t)는 시간 t에서의 입력
2. y(t)는 출력
3. x(t)는 시간 t에서의 상태 벡터
4. dx(t)는 연속시간 시스템으로 상태의 시간 미분
5. A,B,C,D는 파라미터 p에 대한 상태공간 행렬로 현재 파리미터 값 p에 대한 시스템이 어떤 선형 모델인지 정의
6. p=p(t)는 스케줄링 파라미터로 시간에 따라 변하는 측정 가능한 값으로 시스템의 선형성에 영향을 주는 외부 변수
7. x₀(p), u₀(p), y₀(p), dx₀(p)는 앞서 말한 파라미터 p에서의 기준값을 의미하여 상태, 입력, 출력, 기준 상태 변화를 p에서의 기준으로 값이 바뀜

예제1 - LPV System 블록을 사용하여 선형 파라미터 가변 시스템 시뮬레이션하기

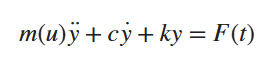
해당 부분에 질량이 외부 하중 명령의 함수에 의해 변하는 선형 질량 스프링 댐퍼 시스템으로 가정함 해당 방정식은 상단과 같음

• m : 외부 명령 u에 종속된 질량임
• c : 감쇠비
• k : 스프링의 강성
• u : 1볼트에서 10볼트로 입력값의 범위를 선정
• F(t) : 가해지는 입력

해당 질량과 입력간에 관계는

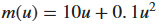
이렇다고 가정함

c = 5;   
k = 300; 
u = 1:10;
m = 10*u + 0.1*u.^2; 

for i = 1:length(u)
   A = [0 1; -k/m(i), -c/m(i)]; 
   B = [0; 1/m(i)];
   C = [1 0];
   sys(:,:,i) = ss(A,B,C,0); 
end

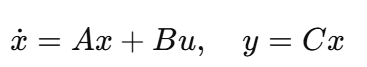
ss(A,B,C,D) 같은경우 상단에 상태방정식을 뜻하는 것임

• A = [0 1; -k/m(i), -c/m(i)]; 해당 부분은 상태공간에 A행렬을 뜻함
• B = [0; 1/m(i)]; 해당 부분은 상태공간에 B행렬을 뜻함
• C = [1 0];

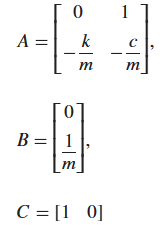
해당식은 이렇게 도입

이것으로 질량의 위치 y(t)를 사용

sys.SamplingGrid = struct('LoadCommand',u);

• 해당것으로 u에 들어가 있는 1~10의 값들을 SamplingGrid를 하여 sys(:,:,i)에 해당하는 파라미터 값과의 연결관계를 matlab에게 알려준다고 생각하면됨

model = "simMSDLPV";
open_system(model);

기존에 있는 simMSDLP모델 변수를 만들고 열는 거임

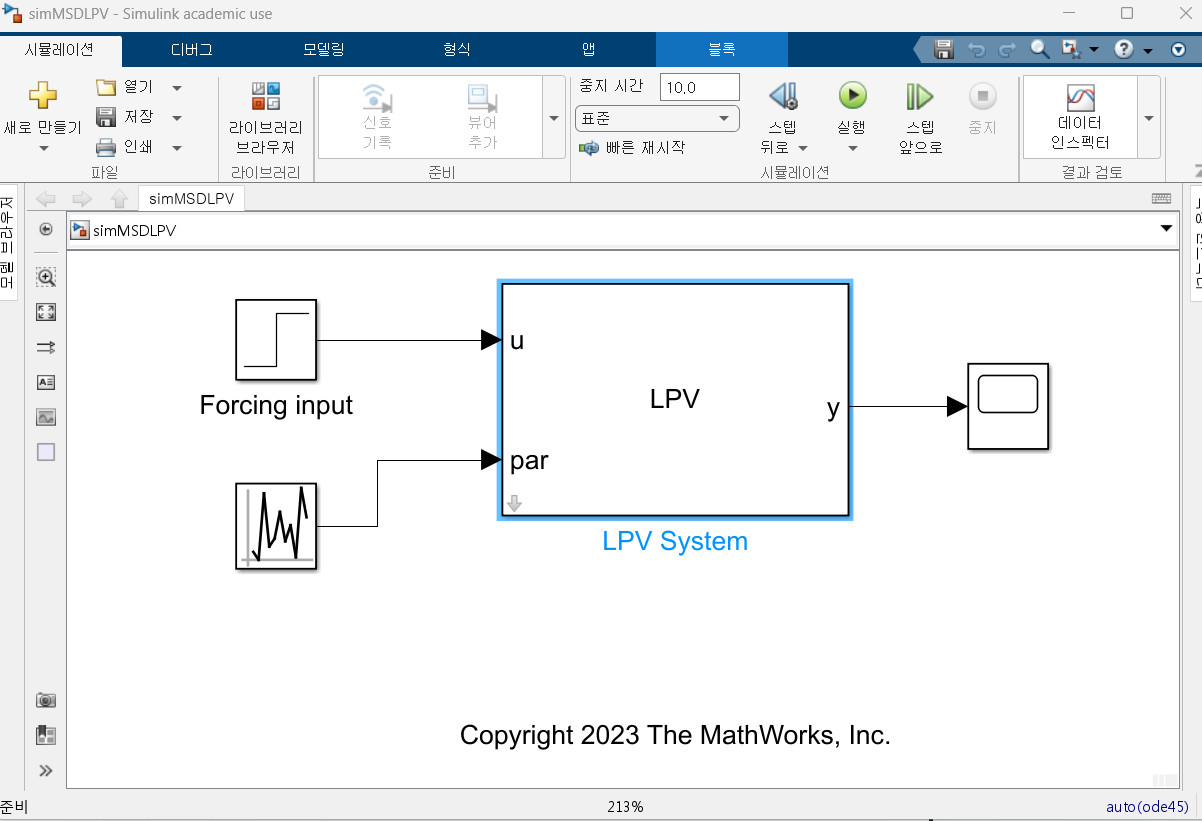
그러면 해당 부분이 나오는데

LPV Block을 확인하면

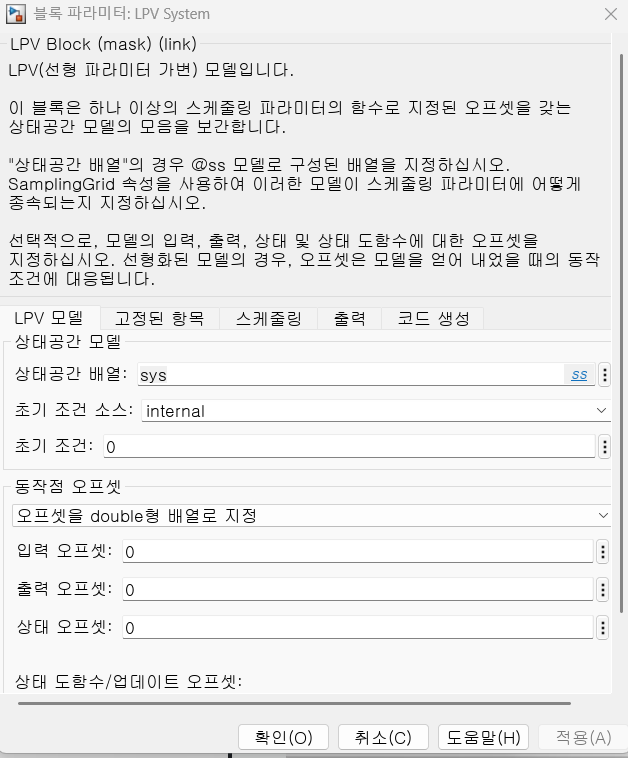
상태공간 배열: sys 기존에 활용한것이고

• internal - Simulink 내부에서 초기 상태 x(0)을 0 또는 지정된 값으로 설정

• external - 입력 포트를 통해 초기 상태를 외부에서 넣을 수 있음

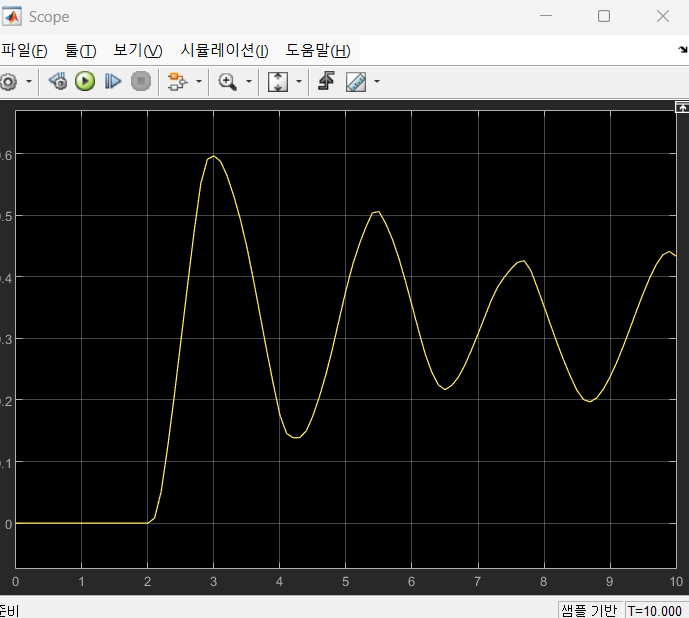
해당결과처럼 나옴

예제2 - 비선형 모델과 LPV 블록 응답 비교하기

참고
https://kr.mathworks.com/help/control/ref/lpvsystem.html