[Paper review] N-HiTS: Neural Hierarchical Interpolation for Time Series Forecasting

해당 논문은 크게 2가지 문제를 동기부여 삼았다.
장기 예측 시나리오에서

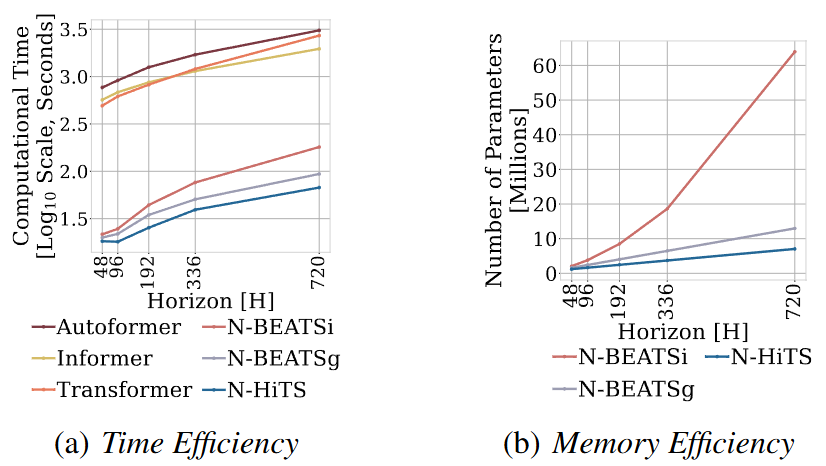
1. 예측기의 변동성
2. 연산 복잡도

위의 문제를 2가지 방법으로 해결하고자 한다.

1. Multi-Rate Data Sampling
2. Hierarchical Interpolation

두 가지 제안 방법론을 살펴고보고자 한다.

제안 방법론

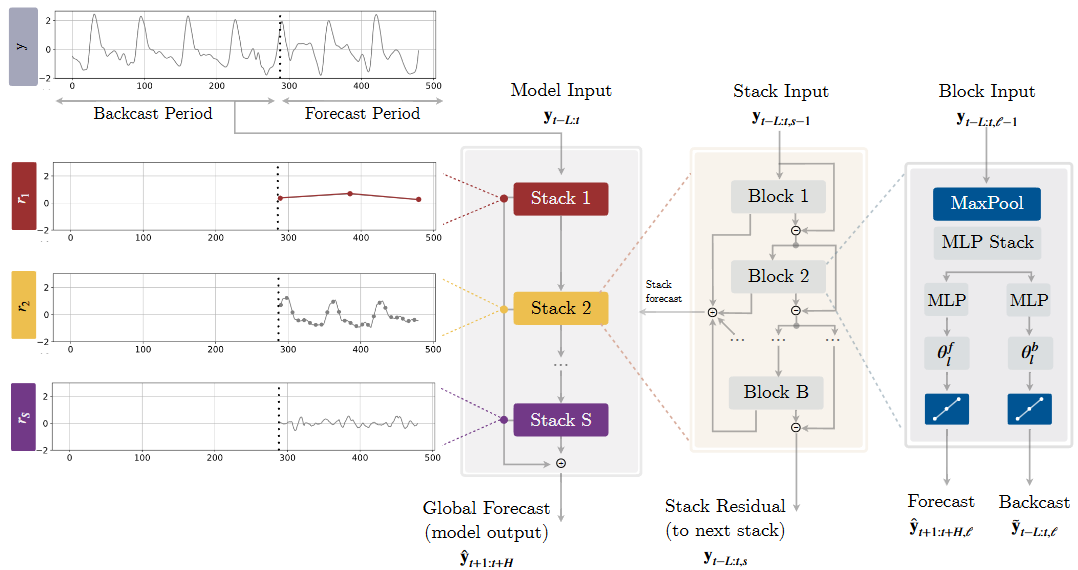
해당 논문의 핵심은 input signal을 multi-rate으로 sampling한 점과 multi-scale 합성으로 예측한 점이다. 본 연구는 N-BEATS에서 발전시켰다.

(1) Multi-rate은 Block Input 그림에서 MaxPool로 조절된다. Kernel size가 클 경우에는 ling-horizon 예측에서 중요한 요소를 집중하게 되고, Kernel size가 작을 경우는 그 반대로 작용하게 된다. 이는 자연스럽게 MLP 입력값의 크기가 작아짐으로 memory footprint가 줄어들게 된다.

(2) Non-Linear Regression으로 MLP Stack을 통과한 값은 Forecast와 Backcast 비선형 예측과정을 거친다. 이때 Forecast는 모두 더해지며, Backcast는 모두 빼는 과정을 거친다. Backcast를 빼는 이유는 이전 레이어에서 다룬 정보를 제외하고 학습하기 위함이라고 한다.

(3) Hierarchical Interpolation은 Transformer에서 L 시점을 보고 H 시점을 바로 예측하는 문제점을 극복하기 위해 temporal interpolation을 제안하였다. 이는 출력 차원 $\theta_f^l=r_eH$을 축소하는 대신, 시간 축에서 값을 보간하여 예측을 수행한다. 보간을 통해 시간 축에서 더 적은 정보로도 원래 $H$ 길이 만큼의 예측 값을 복웒나다. 또한, interpolation coefficients $\gamma_l$를 통해 주파수 대역을 조절한다. 선형 보간기 $g\in C^1$는 time partition $\tau=\{t+1, t+1+1/r_l,...,t+H-1/r_l, t+H\}$ 이다.

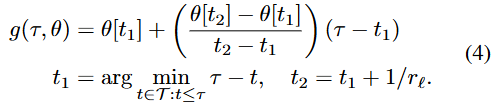
식을 보면 $t_1$은 $\tau$에서 가장 가까운 시점임을 알 수 있다. 이는 1,2,3,... 씩 커져가는 $t$시점 사이를 주파수 크기만큼 사이를 채운다. 따라서, 이를 temporal interpolation이라고 칭하고 approximate long horizons in the presence of smoothness라고도 표현한 것 같다.

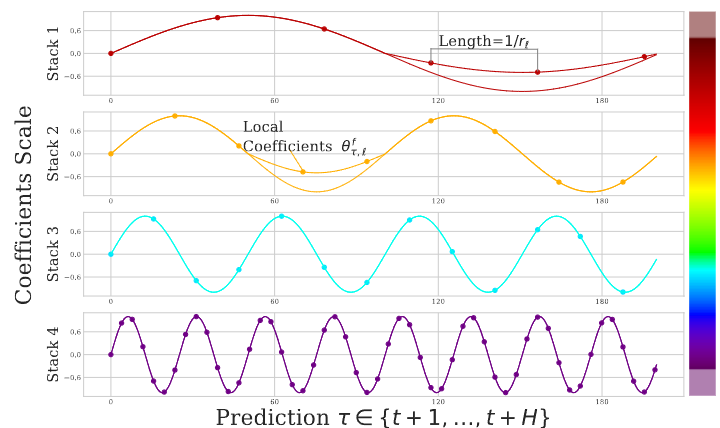
각 Stack별로 저 주파수에서 고주파수 예측을 하는 것을 확인할 수 있다.

실험결과

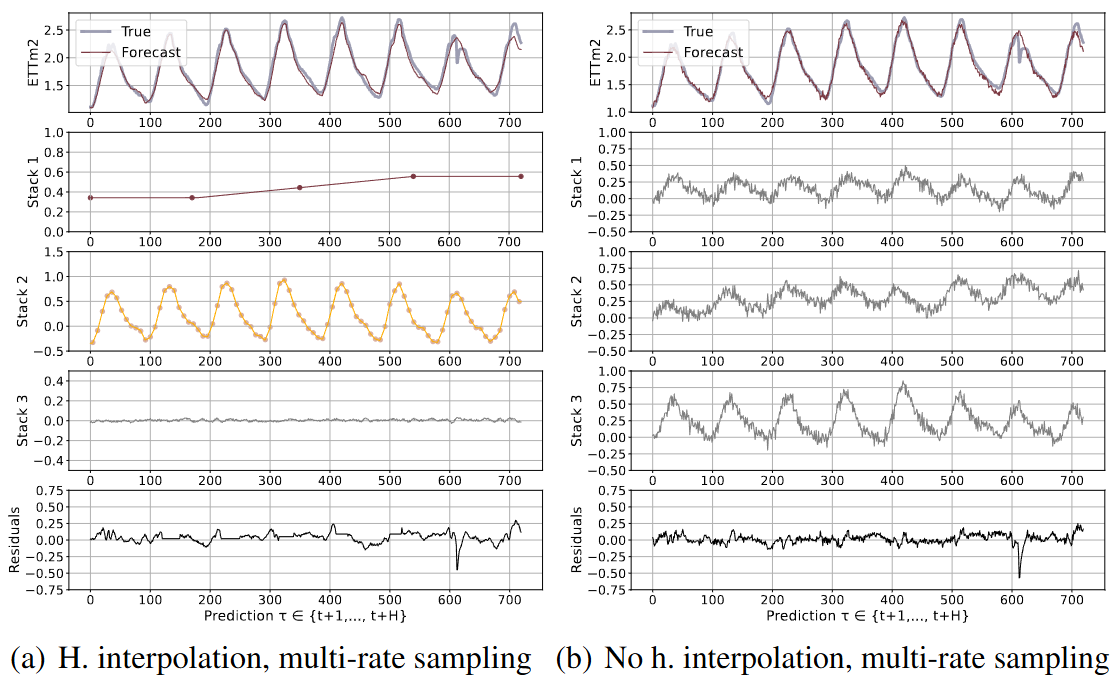
(b)에서 Multi-rate sampling을 하지 않으면, 같은 주파수를 Stack 별로 학습하는 것을 확인할 수 있다. 또한, h. interpolation을 사용하지 않으면 smothness가 떨어지는 것을 확인할 수 있다. 정리하면 계층적 구조는 주파수 간격으로 temporal interpolate과 multi-rate sampling을 stack 구조로 쌓은 것이라고 이해할 수 있다. 그리고 최종적으로 계층적 출력값을 더하여 최종 예측한다.

CODE