1. 개요

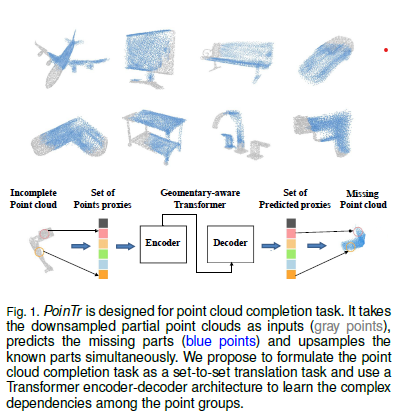
AdaPoinTr는 Point-cloud 완성을 위한 혁신적인 접근 방식을 제시하며, 이를 Set-to-Set 변환 문제로 재구성합니다.
이 모델은 Transformer 아키텍처를 활용하여 3D 기하학적 구조를 효과적으로 학습하고,

• 적응형 쿼리 생성(Adaptive Query Generator) 메커니즘
• 보조 노이즈 제거(Denoising) 작업

을 통해 성능을 크게 향상시킵니다.

주요 성과

• 다양한 불완전한 Point-cloud 상황에서 20% 이상의 성능 향상을 달성
• Point Cloud Completion의 새로운 기준을 설정

방법론

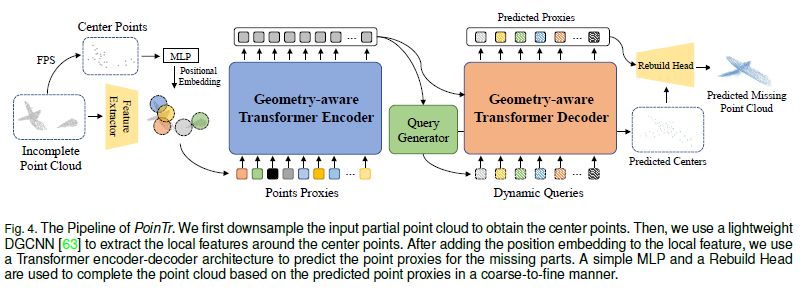
AdaPoinTr는 Transformer 기반 인코더-디코더 아키텍처를 활용하여 포인트 클라우드 완성을 수행합니다.
이 방법은
1. 포인트 클라우드를 순서가 없는 점 집합(Set)으로 표현
2. 입력 데이터를 포인트 프록시(Point Proxy)의 시퀀스(Sequence)로 변환하여 생성

하는 과정을 통해 보다 정확하고 강건한 복원을 가능하게 합니다.

2. Methods

2.1 Set-to-Set Translation with Transformers

Set-to-Set이란 하나의 집합(set)을 다른 집합으로 변환하는 것을 의미합니다. 여기서 집합(set)은 순서가 없는 여러 요소들의 모음을 뜻합니다. 예를 들어, 아래 그림과 같이 Incomplete Point Cloud를 Predicted Missing Point Cloud로 변환하는 과정이 set-to-set translation에 해당합니다.

우리는 먼저 point cloud를 특징 벡터(feature vector) 집합, 즉 point proxy로 변환하는 방법을 제안합니다. Point proxy는 점군 내의 지역(local) 영역을 나타내며, 이에 대한 자세한 내용은 Section 2.2에서 설명하겠습니다.

언어 번역 과정을 비유하자면, 우리는 점군 보완(point cloud completion)을 set-to-set translation 문제로 모델링합니다. Transformer는 불완전한 점군의 point proxy를 입력으로 받아, 누락된 부분의 point proxy를 생성하는 역할을 합니다.

구체적으로, 불완전한 점군을 나타내는 point proxy 집합이 주어졌을 때, 이를 다음과 같이 모델링할 수 있습니다.

$\mathcal{F}=\{F_1,F_2,...,F_N\}$

여기서 (N)은 입력 points의 개수입니다.

Transformer를 이용한 점군 보완 과정은 다음과 같이 정의됩니다.

$\mathcal{V} = \mathcal{M}_E(\mathcal{F}),$
$\mathcal{H} = \mathcal{M}_D(\mathcal{Q}, \mathcal{V})$

여기서:

• $\mathcal{M}_E$와 $\mathcal{M}_D$는 각각 encoder와 decoder 모델을 의미합니다.
• $\mathcal{V}=\{V_1,V_2,...,V_N\}$는 인코더의 출력(feature vectors)입니다.
• $\mathcal{Q}=\{Q_1,Q_2,...,Q_M\}$는 본 논문에서 제안하는 dynamic queries이며, 디코더의 입력으로 사용됩니다.
• $M$은 Query 개수이며, 사용자가 임의로 설정할 수 있습니다.
• $\mathcal{H}=\{H_1,H_2,...,H_M\}$는 네트워크가 예측하여 생성한 point cloud의 point proxy입니다.

이렇게 생성된 point proxy ($\mathcal{H}$)는 multi-scale 방식으로 rebuild하여 최종 point cloud를 생성합니다. Rebuild 과정에 대한 자세한 내용은 Section 2.5에서 설명하겠습니다.

---

2.2 Point Proxy

2.2.1. Transformer와 3D 포인트 클라우드의 차이

Transformer 모델은 원래 NLP(자연어 처리)에서 사용되며, 1D 시퀀스 형태의 입력(예: 단어 임베딩)을 처리합니다.
반면, 3D 포인트 클라우드는 다차원(3D 좌표) 데이터이므로 Transformer에 바로 적용하기 어렵습니다.

2.2.2. 3D 포인트 클라우드를 Transformer 입력으로 변환하는 문제

가장 단순한 방법은 xyz 좌표를 직접 Transformer에 입력하는 것입니다.
그러나 Transformer의 계산 복잡도는 시퀀스 길이에 대해 (O(N^2)) (제곱, quadratic)으로 증가하기 때문에,
이 방법은 계산 비용이 너무 커서 비효율적입니다.
👉 따라서, 더 효율적인 변환 방법이 필요합니다.

2.2.3. 해결 방법: Point Proxy 사용

포인트 프록시(Point Proxy)란 원본 포인트 클라우드의 일부를 대표하는 벡터입니다.
즉, 모든 점을 Transformer에 입력하는 대신, 대표적인 몇 개의 점을 선택하여 입력하는 방식입니다.
이를 위해 두 가지 기법을 사용합니다.

1. FPS (Furthest Point Sampling, 최외곽 점 샘플링)
   • 포인트 클라우드에서 (N)개의 대표적인 중심점(point centers)을 선택합니다.
2. DGCNN (Dynamic Graph CNN) 활용
   • 선택된 중심점들의 주변 지역 특징을 추출하여,
   • 각 포인트 프록시(대표점)에 대한 특징 벡터(feature vector)를 생성합니다.

2.2.4. 포인트 프록시의 특징 벡터 생성

포인트 프록시 (F_i)는 다음과 같이 계산됩니다.

$F_{i}=F'_{i}+\varphi(p_{i})$

• $F'_i$: DGCNN을 이용해 추출한 지역 특징 벡터
• $\phi(p_i)$: MLP(다층 퍼셉트론)을 이용해 위치 정보를 추가적으로 인코딩한 벡터

이렇게 하면,

• 첫 번째 항 $F'_i$는 해당 지역의 의미적(semantic) 정보를 포함하고,
• 두 번째 항 $\phi(p_i)$는 Transformer에서 사용하는 위치 임베딩(Position Embedding) 개념을 적용하여,
  전역적인 위치 정보까지 고려할 수 있습니다.

---

2.3 Geometry-Aware Transformer Block

Transformer 모델을 비전(영상) 작업에 적용하는 데에는 몇 가지 어려움이 있습니다. 그중 하나는 Self-Attention(자가-어텐션) 메커니즘이 기존 CNN(합성곱 신경망)과 같은 비전 모델에서 제공하는 유도 편향(Inductive Bias)을 갖고 있지 않다는 점입니다. CNN은 이미지나 3D 데이터의 구조적 특성을 명시적으로 모델링하는 반면, Transformer는 이러한 구조를 자연스럽게 학습하기 어렵습니다.

이 문제를 해결하기 위해 3D 포인트 클라우드의 기하학적 구조를 잘 활용할 수 있도록 Geometry-Aware Block(기하학적 구조 인식 블록)을 설계했습니다. 이 블록은 Transformer의 어텐션 모듈과 결합할 수 있는 플러그앤플레이(plug-and-play) 방식의 모듈로, 기존 Transformer 아키텍처에 쉽게 적용할 수 있습니다.

기존 Self-Attention 모듈은 특징(feature) 간의 유사도를 기반으로 의미론적 관계를 학습합니다. 하지만 우리가 제안하는 Geometry-Aware Block은 k-Nearest Neighbors (kNN) 방식을 활용하여 포인트 클라우드 내 기하학적 관계를 학습합니다.
기하학적 관계를 학습하는 과정은 다음과 같습니다.

$\phi(V_{i})$ = $\mathcal{M}$$(Linear([V_{i},V_{j}-V_{i}]),\quad \forall_{j}:p^{j}_{k}\in\kappa(p^{i}_{Q})$$
여기서:

• $\mathcal{M}$ : 최대 풀링(max-pooling) 연산
• $V$ : 입력 특징(feature)
• $p_Q$ : 질의 포인트(query point)
• $p_k$ : ( p_Q ) 주변의 k개의 이웃(Neighborhood)

즉, 질의 포인트 ( p_Q ) 주변의 k개 이웃 포인트 ( p_k )의 특징을 수집한 후, 선형 변환(Linear Transformation)과 최대 풀링 연산을 적용하여 지역적인 기하학적 구조를 학습합니다.

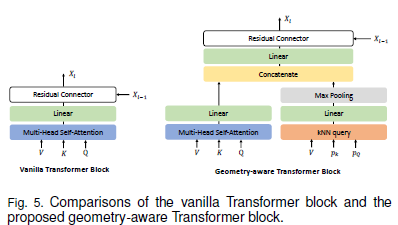
이 방식은 DGCNN(Dynamic Graph CNN)의 아이디어를 따릅니다.
즉, kNN을 활용하여 로컬 기하학적 구조를 학습한 후, 위 그림과 같이 Self-Attention을 통해 학습한 특징과 결합(Concatenation)하여 최종 출력 특징을 생성합니다.

이 방식은 기존 Transformer 모델에 쉽게 적용할 수 있으며, 포인트 클라우드 데이터의 3D 기하학적 정보를 효과적으로 학습하는 데 도움을 줍니다.
결과적으로, Transformer가 비전 데이터에서 더 나은 성능을 발휘할 수 있도록 지원합니다.

---

2.4 Query Generator

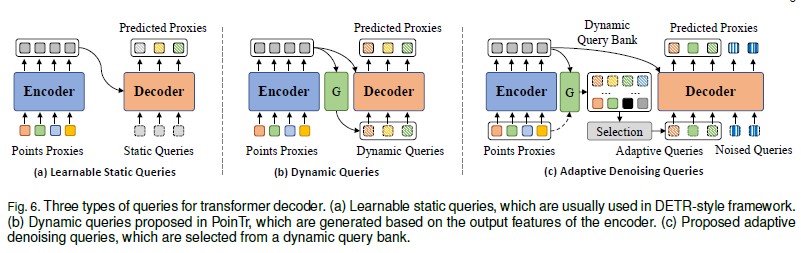
Transformer 기반의 포인트 클라우드 복원 모델에서 쿼리(Q)는 예측된 프록시(proxy)의 초기 상태 역할을 합니다.
즉, Q가 올바르게 포인트 클라우드의 전체 윤곽을 반영해야만 모델이 더욱 정확한 복원을 수행할 수 있습니다.

이를 위해, 우리는 쿼리 생성기(Query Generator) 모듈을 설계하여 인코더 출력 V를 기반으로 동적으로 쿼리 임베딩을 생성하는 방식을 제안합니다.

쿼리 생성 과정은 다음과 같은 단계로 이루어집니다.

• 인코더 출력 V 요약(Summarization)

  • 인코더의 출력 V를 선형 변환(Linear Projection)하여 더 높은 차원으로 매핑
  • 이후, 맥스 풀링(Max-Pooling) 연산을 적용하여 전체 특징을 요약

• 쿼리 좌표 생성(Query Coordinates Generation)

  • 선형 변환층을 사용하여 M × 3 차원의 특징을 생성
  • 이를 M개의 좌표 $\mathcal{C} = \{c₁, c₂, …, c_M\}$ 로 변환

• 최종 쿼리 임베딩 생성(Query Embedding Generation)

  • 인코더의 글로벌 특징과 좌표를 결합(Concatenation)
  • 다층 퍼셉트론(MLP)을 사용하여 최종적으로 쿼리 임베딩 $\mathcal{Q} = \{Q₁, Q₂, …, Q_M\}$을 생성

수식 표현
$\mathcal{C}$$=$$\mathcal{P}(\mathcal{M}(Linear(\mathcal{V})),\quad$$\mathcal{Q}$$=$$MLP([\mathcal{C},\mathcal{M}(Linear(\mathcal{V})])$

여기서:

• $\mathcal{M}$ : 맥스 풀링(Max-Pooling) 연산
• $\mathcal{P}$ : 좌표 변환(Projection) 연산
• $\mathcal{V}$ : 인코더의 출력 특징
• $\mathcal{Q}$ : 최종 쿼리 임베딩

이 방식은 쿼리를 정적으로 설정하는 대신, 입력 데이터(V)를 기반으로 동적으로 생성하는 접근법을 활용합니다.
이를 통해, 예측된 포인트 클라우드가 원본의 구조를 더 정확하게 반영할 수 있도록 보장할 수 있습니다.

---

2.5 다중 스케일 포인트 클라우드 생성 (Multi-Scale Point Cloud Generation)

인코더-디코더 네트워크의 목적은 불완전한 포인트 클라우드에서 누락된 부분을 예측하는 것입니다. 그러나 Transformer 디코더로부터는 누락된 proxy에 대한 예측만 얻을 수 있습니다. 따라서, 우리는 다중 스케일 포인트 클라우드 생성 프레임워크를 제안하여 완전한 해상도로 누락된 포인트 클라우드를 복원합니다.

핵심 아이디어

• 중복 계산 최소화: 쿼리 생성기(Query Generator)가 생성한 M개의 좌표를 누락된 포인트 클라우드의 지역 중심(Local Centers)으로 재사용합니다.
• 세부 복원: 그런 다음, FoldingNet과 유사한 재구성 헤드(Reconstruction Head) $f$를 사용하여, 예측된 프록시를 중심으로 세부적인 지역 형태(Local Shape)를 복원합니다.

수식 표현
$\mathcal{P}_i=f(\mathcal{H}_i)+c_i,$ $\quad i=1,2,...,M$
여기서:

• $\mathcal{P}_i$: 중심 $c_i$ 주변에 복원된 포인트 집합
• $\mathcal{H}_i$: 중심 $c_i$에 대응하는 특징(feature)
• $f$: 재구성 함수 (FoldingNet 스타일)

전체 포인트 클라우드 완성

• 포인트 클라우드의 누락된 부분만 예측하고 이를 입력 포인트 클라우드와 결합하여 완전한 객체를 구성합니다.
• 예측된 프록시와 복원된 포인트 클라우드는 모두 훈련 과정에서 감독 학습(supervised learning)을 받습니다.

---

2.6 적응형 노이즈 제거 쿼리 (Adaptive Denoising Queries)

문제점
$\mathbb{R}^3$공간에서 입력된 점과 예측된 누락된 점을 단순히 연결(concatenation) 하는 방식은 쉽지만,
두 부분을 별개로 다루어 불연속적이고 고르지 않은 Point-cloud이 생성되는 문제가 발생합니다.

• 누락된 부분: 재구성 헤드에서 생성
• 기존의 알려진 부분: 백프로젝션 방식 또는 LiDAR 센서로 획득

이 문제를 해결하기 위해 일반적인 방법은 연결 후 정제 모듈(refinement modules)을 추가하는 것이지만,
이는 추가적인 파라미터와 지연(latency)을 초래합니다.

AdaPoinTr의 해결책
우리는 AdaPoinTr(PoinTr + Adaptive Denoising Queries)를 제안합니다.
이는 기존 방식과 달리 Point-cloud 자체가 아닌 점 프록시(point proxy)를 연결하는 방식을 사용합니다.
이를 통해:

• 두 부분을 통합적으로 재구성할 수 있음
• 추가적인 정제 파라미터 없이도 성능 향상 가능

추가적인 성능 개선: Adaptive Denoising Queries
노이즈 제거(denoising) 작업을 도입하여 모델의 효율성과 견고성을 대폭 향상시켰습니다.

Adaptive Denoising Queries는 두 가지 주요 구성 요소로 이루어져 있습니다.
1. 적응형 쿼리 생성 메커니즘 (Adaptive queries generation mechanism)
2. 보조 노이즈 제거 작업 (Auxiliary denoising task)

2.6.1 적응형 쿼리 생성 (Adaptive Query Generation)

• 기존 쿼리 생성기(Query Generator)를 개선하여 동적 쿼리 뱅크 $\mathcal{B}$ 생성

• 입력:

  • 인코더 아웃풋 $\mathcal{V}$
  • 인풋 포인트 프록시 $\mathcal{F}$

• 동적 쿼리 뱅크 구성:

  • $\mathcal{Q_I}$: 입력 proxy $\mathcal{F}$로부터 추출
  • $\mathcal{Q_O}$: 누락된 proxy의 초기 상태로 사용

• 처리 과정:

  1. $\mathcal{V}$와 $\mathcal{F}$를 고차원으로 선형 투영(linear projection) 후, 각각 Max-pooling 수행
  2. $M_I × 3$, $M_O × 3$ 차원으로 좌표 투영(coordinate projection) 후 좌표 생성
     $\mathcal{C^I} = \{c^I_1, c^I_2, …, c^{I}_{M_I}\}$
     $\mathcal{C^O} = \{c^O_1, c^O_2, …, c^{O}_{M_O}\}$
  3. 좌표 + 요약된 특징을 MLP에 입력하여 쿼리 생성:
     $\mathcal{C^I} = \mathcal{P_I}(\mathcal{M}(\mathcal{W_I}(\mathcal{F})), \quad \mathcal{Q_I} = MLP([\mathcal{C^I}, \mathcal{M}(\mathcal{W_I}(\mathcal{F}))]$
     $\mathcal{C^O} = \mathcal{P_O}(\mathcal{M}(\mathcal{W_O}(\mathcal{V})), \quad \mathcal{Q_O} = MLP([\mathcal{C^O}, \mathcal{M}(\mathcal{W_O}(\mathcal{V}))]$
     여기서, $\mathcal{M}, \mathcal{P_I}, \mathcal{P_O}, \mathcal{W_I}, \mathcal{W_O}$는 max-pooling 연산, 인풋, 아웃풋의 좌표 투영(coordinate projection), 그리고 인풋, 아웃풋의 선영 투영(linear projection)을 나타냄.

• 쿼리 선택:

  • 경량화된 스코어링 모듈 $\mathcal{S}$로 쿼리 뱅크 $\mathcal{B}$ 내 쿼리를 스코어링 및 상위 $M$개 선택
  • 최종적으로 쿼리 $\mathcal{Q}$ 및 좌표 $\mathcal{C}$로 구성

---

2.6.2) 보조 노이즈 제거 작업 (Auxiliary Denoising Task)

• Transformer 디코더의 문제:

  • 초기 쿼리 품질 저하로 훈련 초기에 불안정한 성능 (Loss 수렴의 불안정)
  • 다중 스케일 포인트 클라우드 생성으로 일부 개선, 하지만 한계 존재

• 개선 방안:

  • 노이즈 쿼리 도입: 적응형 쿼리와 함께 디코더에 입력
  • 무작위 노이즈를 Groundtruth 중심점 $c^{gt}$에 더함
    $\hat{c}_{i}^{gt}=n_{i}+c_{i}^{gt}$
  • 노이즈 쿼리 생성:
    $\hat{\mathcal{Q}} = MLP([\hat{C}, \mathcal{M}(Linear(\mathcal{V})])$
    여기서 $\mathcal{Q_I}, \mathcal{Q_O}$는 $MLP$를 공유하므로 같이 생성될 수 있습니다.

• 효과:

  1. 항상 고품질 쿼리 존재 보장
  2. 디코더의 초기 쿼리 강건성 향상

• Knowledge leakage 방지:

  • 노이즈 쿼리 $\hat{\mathcal{Q}}$와 일반 쿼리 $\mathcal{Q}$간 Self-attention 마스크 적용:
    $m_{ij}=\begin{cases}0 &\text{if }q_i\in \hat{\mathcal{Q}}, q_j\in \mathcal{Q}\\1 & \text{if } otherwise\end{cases}$
    

• 최종 출력:
  • Transformer 디코더 $\mathcal{M}_D$를 통해 쿼리 $\mathcal{\hat{Q}}$를 프로시 $\hat{\mathcal{H}}$로 변환:
    $[\mathcal{H}, \hat{\mathcal{H}}] = \mathcal{M}_D([\mathcal{Q}, \mathcal{\hat{Q}}], \mathcal{V})$
  • 노이즈 프로시 $\hat{\mathcal{H}}$을 $f$로 rebuilt 해서 local shape $\hat{\mathcal{P}_i}$를 생성합니다. :
    $\hat{\mathcal{P}_i}=f(\hat{\mathcal{H}})+\hat{c}_{i}^{gt}$

---

2.7 Optimization

2.7.1) 손실 함수의 필요성

• 점군(Point Cloud)은 순서가 없는(unordered) 데이터 구조이므로, 일반적인 유클리드 거리(예: ℓ2 거리)를 사용한 손실 함수는 적절하지 않음.
• 대신, Chamfer Distance (CD)와 Earth Mover’s Distance (EMD)가 점군의 순서에 영향을 받지 않는 손실 함수로 사용될 수 있음.
• 논문에서는 Chamfer Distance (CD)를 선택함. 이유는 O(N logN)의 시간 복잡도로, 계산이 상대적으로 빠르기 때문.

2.7.2) Chamfer Distance 기반 손실 함수

점군 완성(Point Cloud Completion)을 위해 두 가지 주요 손실 함수를 정의:

(1) $J_0$: Low-resolution (Sparse) Completion Loss
-$\mathcal{C}$: 복원된 로컬 중심점들 ($n_\mathcal{C}$개)
-$\mathcal{G}$: Ground Truth (실제) 완전한 점군 ($n_\mathcal{G}$개)

$J_0 = \frac{1}{n_\mathcal{C}} \sum_{c \in \mathcal{C}} \min_{g \in \mathcal{G}} ||c - g|| + \frac{1}{n_\mathcal{G}} \sum_{g \in \mathcal{G}} \min_{c \in \mathcal{C}} ||g - c||$

설명:

• 첫 번째 항: 복원된 점$c$가 실제 점군$G$내에서 가장 가까운 점$g$와의 거리 합.
• 두 번째 항: 실제 점군의 점$g$가 복원된 점군$C$내에서 가장 가까운 점$c$와의 거리 합.
• 즉, 복원된 점군과 실제 점군이 서로 가까워지도록 학습하는 목적.

(2) $J_1$: High-resolution (Dense) Completion Loss
-$\mathcal{P}$: 복원된 전체 점군 ($n_\mathcal{P}$개)
-$\mathcal{G}$: Ground Truth 완전한 점군 ($n_\mathcal{G}$개)

$J_1 = \frac{1}{n_\mathcal{P}} \sum_{p \in \mathcal{P}} \min_{g \in \mathcal{G}} ||p - g|| + \frac{1}{n_\mathcal{G}} \sum_{g \in \mathcal{G}} \min_{p \in \mathcal{P}} ||g - p||$

설명:
-$J_1$는 보다 고해상도(high-resolution) 복원을 평가하는 손실.
-$J_0$와 같은 구조이지만, 더 많은 포인트($P$)를 고려하여 전체적인 점 분포를 더욱 정밀하게 복원하도록 유도.

2.7.3) 보조 노이즈 제거 (Denoising) 손실 함수

• 점군 복원 모델이 노이즈가 있는 입력 데이터에도 강건함(Robust)을 유지하도록, 보조적인 손실 함수를 추가함.
• 노이즈 추가된 입력$\hat{\mathcal{Q}}_i$와 노이즈 포함 중심점$\hat{c}^{gt}_{i} = n_i + c^{gt}_{i}$사용.
• 목표는 모델이 노이즈$n_i$를 극복하고, 원래의 로컬 형상을 올바르게 복원하는 것.

$J_{\text{denoise}} = \frac{1}{|\hat{\mathcal{P}}_i|} \sum_{c \in \hat{\mathcal{P}}_i} \min_{g \in \mathcal{G}^{gt}_{c_i}} ||c - g|| + \frac{1}{|\mathcal{G}^{gt}_{c_i}|} \sum_{g \in \mathcal{G}^{gt}_{c_i}} \min_{c \in \hat{\mathcal{P}}_i} ||g - c||$

설명:
-$\hat{P}_i$: 노이즈가 추가된 입력을 기반으로 복원된 점군.
-$G_{gt, c_i}$: Ground Truth 로컬 형상.

• Chamfer Distance를 사용하여 원래 로컬 형상과 복원된 점군이 유사해지도록 손실을 설계.

2.7.4) 최종 손실 함수 (Total Loss)

위의 손실 함수들을 모두 합쳐 최종적인 점군 복원 손실 함수를 정의:

$J_{PC} = J_0 + J_1 + \lambda J_{\text{denoise}}$

-$\lambda$: 노이즈 제거 손실에 대한 가중치 (조절 가능).
-$J_0$와$J_1$은 점군 복원 자체를 최적화하며,$J_{\text{denoise}}$는 노이즈에 강건한 모델을 만들기 위한 보조적인 손실.

2.7.5) 결론

• 점군 복원을 위해 Chamfer Distance (CD) 기반의 손실 함수를 사용.
• Sparse ($J_0$)와 Dense ($J_1$) 두 가지 손실 함수를 활용하여 저해상도 및 고해상도 점군을 효과적으로 복원.
• Denoising 손실을 추가하여 모델이 노이즈에도 강건하도록 설계.
• 최종 손실 함수는 $J_0 + J_1 + \lambda J_{\text{denoise}}$의 형태로 구성됨.

이러한 최적화 방법을 통해 모델이 순서가 없는 점군 데이터에서도 의미 있는 복원을 수행할 수 있도록 학습할 수 있습니다.

---

2.8 TECHNICAL DETAILS ON TRANSFORMERS

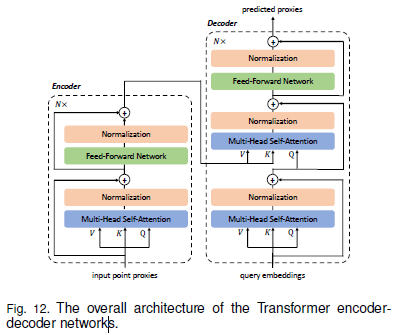
이 논문은 Transformer 기반의 Encoder-Decoder 구조를 사용하여 점군 복원(Point Cloud Completion)을 수행하는 방법을 설명하고 있습니다.
주요 내용을 정리하면 다음과 같습니다.

2.8.1) Transformer Encoder-Decoder 구조

• 전체 Transformer 기반 인코더-디코더 네트워크의 구조는 Fig. 12에 나타나 있음.
• 입력 데이터(점군 프록시, Point Proxies)는 Transformer Encoder를 통과하여 특징을 추출.
• Encoder는 N개의 Multi-Head Self-Attention Layer + Feed-Forward Network (FFN) Layers로 구성됨.
• Decoder는:
  • Query Embeddings와 Encoder Memory를 입력으로 받아
  • N개의 Multi-Head Self-Attention + Decoder-Encoder Attention + FFN Layers를 거쳐
  • 최종적으로 결측된 점군을 예측함.
• 실험에서는 일반적인 설정을 따르기 위해 N=6으로 고정.

2.8.2) Multi-Head Attention (MHA) 기법

Multi-Head Attention (MHA)은 모델이 다양한 위치에서 여러 표현 서브스페이스(subspaces)에 동시에 주의를 기울일 수 있도록 하는 메커니즘.

(1) Multi-Head Attention 수식
$\text{MultiHead}(Q, K, V) = W^O \text{Concat}(\text{head}_1, ..., \text{head}_h)$

• $W^O$ : 출력 선형 변환에 사용되는 가중치.
• 각 헤드(head)의 특징 표현은 다음과 같이 계산됨:

$\text{head}_i = \text{softmax} \left( \frac{Q W^Q_i (K W^K_i)^T}{\sqrt{d_k}} \right) V W^V_i$

• $W^Q_i$, $W^K_i$, $W^V_i$ : 입력 데이터를 서로 다른 표현 공간(subspaces)으로 투영하는 선형 변환 가중치.
• $d_k$ : 입력 특징의 차원.

설명:

• Query ($Q$), Key ($K$), Value ($V$)를 선형 변환 후,
• Key와 Query의 내적을 통해 어텐션 가중치(attention weights)를 구하고,
• Softmax를 통해 확률값을 생성한 뒤,
• Value에 적용하여 최종적인 출력 벡터를 생성.
• 여러 개의 Attention Head를 병렬로 수행한 후, 최종적으로 선형 변환하여 최종 출력 생성.

---

2.8.3) Feed-Forward Network (FFN)

• Transformer의 FFN 구조는 기존 논문 (Vaswani et al., Attention is All You Need)을 따름.
• 구성:
  • 두 개의 선형 계층 (Linear Layers)
  • ReLU 활성화 함수 (ReLU Activation)
  • Dropout 레이어 추가하여 과적합 방지.

2.8.4) 결론

• Transformer 기반의 Encoder-Decoder 구조를 활용하여 점군 복원 수행.
• Multi-Head Attention을 사용하여 다양한 위치에서의 정보를 동시에 학습.
• Feed-Forward Network (FFN)을 사용하여 비선형 변환을 통한 특징 학습을 수행.
• 실험에서는 Transformer의 일반적인 설정을 따라 N=6으로 설정.

이 방식은 기존 CNN 기반 방법들보다 순서가 없는 점군 데이터에서도 효과적으로 학습할 수 있는 장점을 가짐!

3. Results

3.1 Qualitative Results

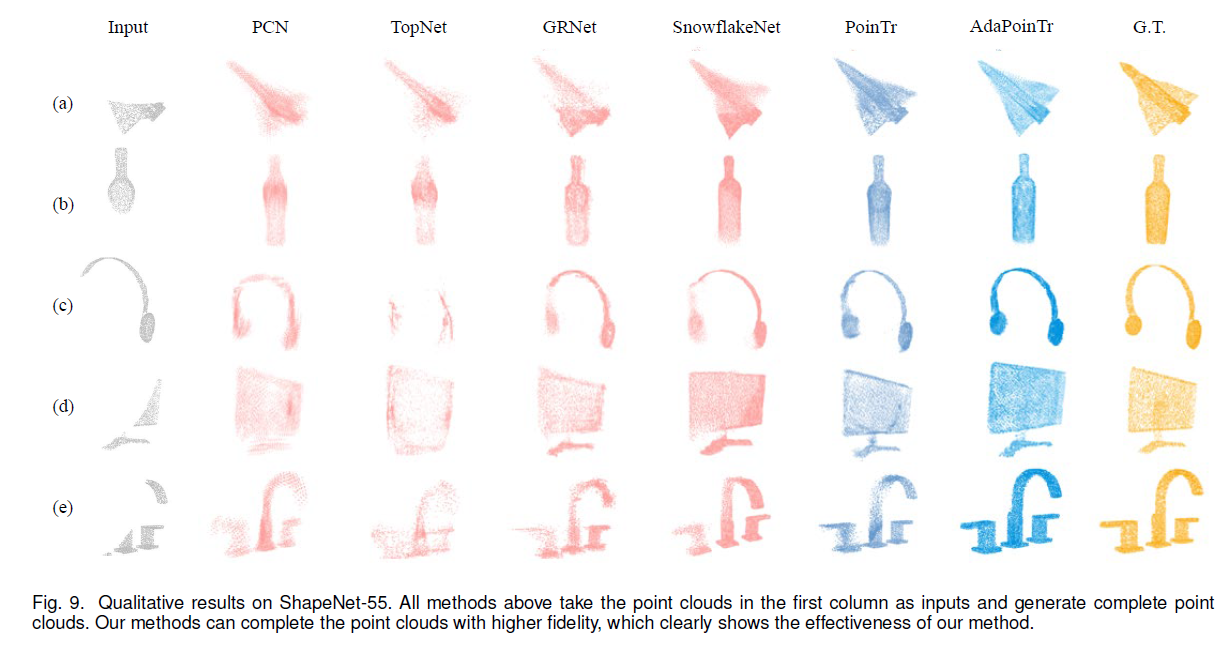
위 그림에서 다양한 방법의 결과를 비교하며, 작성자가 제안한 방법이 더 우수하다는 점을 설명하고 있습니다.

• 비교 실험: 여러 방법을 사용하여 데이터 복원(completion) 결과를 비교했습니다.
• 예시 설명: (a) 입력 데이터는 기하학적 정보(geometric information)가 거의 사라져서 원래 비행기인지 인식하기 어려운 상태입니다.
• 다른 방법의 한계: 기존 방법들은 대략적인 형태만 복원할 수 있으며, 날개의 윤곽 등 세부적인 기하학적 정보가 부족합니다.
• 제안한 방법의 장점: 제안된 방법은 더 높은 정확도로 포인트 클라우드(point cloud)를 복원하며, 세부 정보를 더 잘 유지할 수 있습니다.
• 결론: 제안된 방법이 다양한 불완전한 입력 데이터에도 더 강인하고 세부 정보를 복원하는 능력이 뛰어납니다.

3.1 Model Design Anlysis

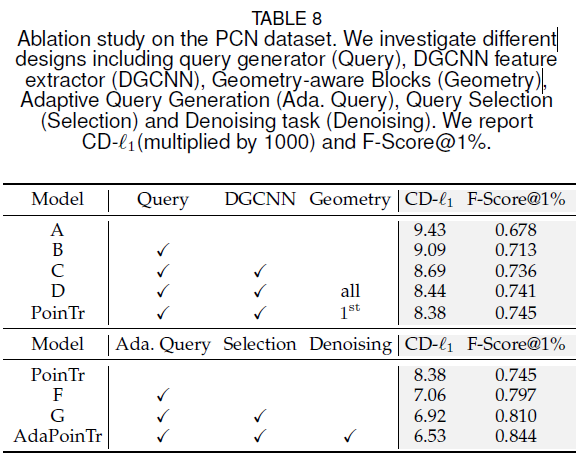
AdaPoinTr 모델의 설계를 분석하기 위해, 주요 구성 요소에 대한 Ablation Study(소거 실험)를 진행했습니다. 결과는 Table 8에 요약되어 있습니다.

기본 모델(A)

• Baseline Model A:
  • Transformer 기반 포인트 클라우드 복원 모델로, Encoder-Decoder 구조를 사용.
  • 포인트 프록시(point proxy)를 직접 포인트 클라우드에서 추출하는 DGCNN 단일층 모델을 사용.
  • Chamfer Distance (CD-1): 9.43, F-Score@1%: 0.678

---

점진적 성능 향상 과정

모델 B: Query Generator 추가

• Query Generator를 Encoder와 Decoder 사이에 추가
  → CD 개선 (9.43 → 9.09)

모델 C: DGCNN Feature Extractor 추가

• DGCNN을 사용하여 포인트 클라우드에서 특징 추출
  → 성능 대폭 향상 (CD 8.69, F-Score 0.736)

모델 D: Geometric Block 추가

• 모든 Transformer 블록에 Geometric Block 추가
  → 성능 향상 (CD 8.44, F-Score 0.741)
• PoinTr: Geometric Block을 모든 Transformer 블록이 아닌 첫 번째 블록에만 적용
  → 성능 미세 개선 (CD 8.38, F-Score 0.745)
  과적합 방지 효과, 기하학적 구조의 유도 편향(inductive bias) 역할만으로 충분

---

AdaPoinTr 모델로 발전

모델 F: Adaptive Query Generation 추가

• Adaptive Query Generation 적용
  → 성능 대폭 향상 (CD 7.06, F-Score 0.797)

모델 G: Query Selection 추가

• Query Selection 추가
  → CD 6.92, F-Score 0.810

최종 모델 - AdaPoinTr

• Denoising Task 추가
  → 최고 성능 달성 (CD 6.53, F-Score 0.844)
  → 포인트 클라우드 복원 분야에서 State-of-the-art (최신 최고 성능)

---

결론

• Ablation Study를 통해 각 구성 요소가 성능을 개선하는 역할을 확인함.
• AdaPoinTr 모델이 가장 높은 성능 (CD 6.53, F-Score 0.844)을 기록
• 특히 Adaptive Query Generation, Query Selection, Denoising Task가 가장 큰 기여를 함.

---

4. CONCLUSION

본 논문에서는 PoinTr라는 새로운 아키텍처를 제안하여, 포인트 클라우드 복원(task) 문제를 Set-to-Set Translation 문제로 변환하였습니다.

주요 성과

• Transformer 모델을 성공적으로 적용하여 성능을 대폭 향상시켰으며, 최신 최고 성능(State-of-the-Art, SOTA)을 달성하였습니다.
• 보다 다양한 객체의 포인트 클라우드 복원을 평가하기 위해 4개의 새로운 벤치마크를 제시하였습니다.
• 또한, PoinTr가 장면 수준(Scene-Level) 작업에도 유용함을 검증하였습니다.

향후 연구 방향

• PoinTr의 도입이 해당 연구 분야의 연구자들에게 영감을 줄 것으로 기대합니다.
• Transformer 아키텍처를 보다 다양한 3D 작업에 확장하는 것이 흥미로운 연구 방향이 될 것입니다.