DGCNN (Dynamic Graph CNN for Learning on Point Clouds) 리뷰

Bean·2025년 4월 13일

3DData 3DDeepLearning Computer_Vision DGCNN DeepLearning EdgeConv GraphNeuralNetwork MachineLearning PointCloud PointCloudProcessing PointNet SemanticSegmentation 그래프신경망 딥러닝 인공지능 포인트클라우드

논문 리뷰

목록 보기

5/15

1. 서론 (Introduction)

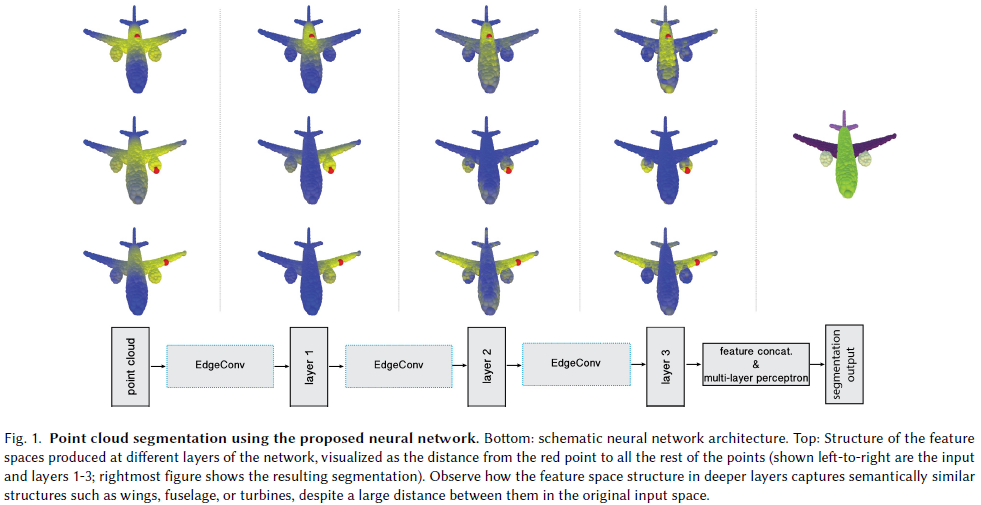
포인트 클라우드란?

2D 또는 3D 공간에서 점들로 구성된 가장 단순한 형태의 데이터 표현.
LiDAR 스캐너나 스테레오 카메라 같은 3D 센서를 통해 생성됨.
최근에는 복잡한 메시 재구성이나 노이즈 제거를 생략하고, 포인트 클라우드를 직접 처리하는 경우가 많음.

활용 분야

실내 내비게이션
자율주행차
로봇공학
3D 형태 합성 및 모델링

포인트 클라우드 처리의 새로운 요구

단순한 기하학적 특징(예: 모서리, 평면)을 찾는 것을 넘어서, 의미 기반 정보(semantic cue)와 기능적 특성(affordance)을 분석해야 함.
이는 기존의 수치해석 기하학으로는 어렵고, 기계 학습 기반 방법이 요구됨.

분류(Classification)와 분할(Segmentation)

전통적인 방식: 수작업으로 설계된 기하 기반 특징 사용.
최근 트렌드: 이미지 처리 분야에서의 딥러닝 성공을 바탕으로, 포인트 클라우드에도 데이터 기반 학습 방식 도입.

딥러닝 적용의 어려움

대부분의 신경망은 정형화된 입력 데이터를 요구하지만, 포인트 클라우드는:
- 불규칙하고
- 순서에 영향받지 않음 (Permutation Invariance)
이를 해결하기 위해 3D 그리드 형태로 변환하는 방법이 있으나:
- 양자화 오류(Quantization Artifacts)
- 메모리 낭비 문제 발생
- 고해상도 정보 포착이 어려움

기존 해결책: PointNet

포인트를 독립적으로 처리하고, 대칭 함수로 종합하여 순서 불변성을 확보.
한계점: 포인트 간의 지역적 관계를 반영하지 못함.

EdgeConv: 제안하는 새로운 연산

포인트의 임베딩에서 직접 특징을 추출하지 않고, 이웃 간의 관계(엣지 특징)를 기반으로 학습.
EdgeConv의 특징:
- 이웃 순서에 영향을 받지 않음 (Permutation Invariance)
- 국소 그래프를 구성하고, 엣지를 통해 특징을 학습
- 유클리드 공간과 의미 공간 모두에서 포인트를 그룹화 가능

성능 및 응용

기존 모델에 간단히 통합 가능
변환 없이 기본 PointNet에 적용하여 성능 향상
ModelNet40과 S3DIS 데이터셋에서 분류 및 분할 작업에 대해 최첨단 성능 달성

주요 기여 (Key Contributions)

포인트 클라우드를 위한 새로운 연산 방식 EdgeConv 제안
계층별로 관계 그래프를 동적으로 업데이트하여 의미적 포인트 그룹화 가능
기존 딥러닝 파이프라인에 쉽게 통합 가능
벤치마크 데이터셋에서 최고 성능 입증
코드 공개를 통해 연구 재현성 및 확장성 확보 (https://github.com/WangYueFt/dgcnn)

2. 방법 (Methods)

개요

본 방법은 PointNet과 합성곱 연산(CNN)의 아이디어에서 영감을 받음.
하지만 PointNet처럼 각 포인트를 따로 처리하는 것이 아니라,
국소 이웃 그래프(local neighborhood graph) 를 구성하여,
이웃 포인트 간의 엣지(edge) 를 중심으로 합성곱 유사 연산을 적용함.

EdgeConv 연산

이 연산은 EdgeConv라 불리며,
CNN의 이동 불변성(translation-invariance) 과
비지역 연산의 non-locality 사이 특성을 가짐.

동적 그래프 구성

기존의 그래프 기반 CNN과 달리, 본 방법에서는 그래프가 고정되어 있지 않음.
네트워크 각 층마다 포인트의 k-최근접 이웃(k-NN) 을
현재 임베딩(feature embedding)을 기반으로 다시 계산함.
이렇게 하면, 원래 좌표 기준의 이웃이 아닌, 의미 공간(feature space) 에서의 이웃 관계가 반영됨.
결과적으로 정보가 전체 포인트 클라우드에 비국소적(non-local)으로 확산됨.

2.1 엣지 컨볼루션 (Edge Convolution)

2.1.1. 기본 개념: 포인트 클라우드와 그래프

포인트 클라우드 $X = \{x_1, ..., x_n\}$

$n$ 개의 점으로 이루어진 데이터셋
각 점 $x_i$ 는 $\mathbb{R}^F$ 공간의 벡터 (즉, $F$ 개의 피처를 가짐)
- 보통 $F=3$ 일 때는 3D 좌표: $x_i = (x, y, z)$
- $F$ 가 더 크면 색상(RGB), 노멀 벡터 등의 정보도 포함 가능

신경망에서는?

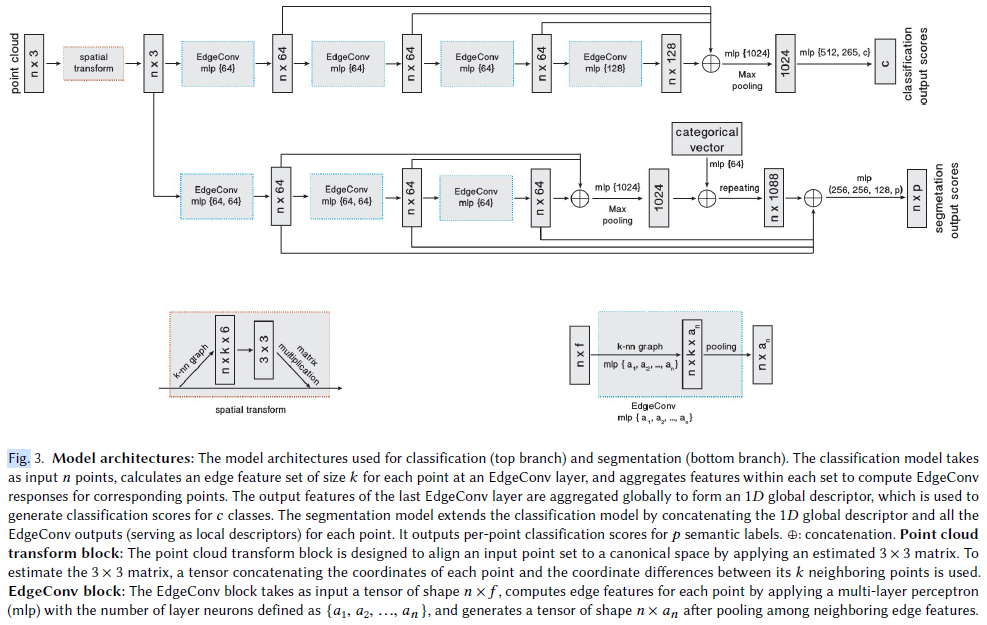
각 layer가 이전 layer의 출력을 받아 처리하므로, 점들의 feature 차원( $F$ )은 변할 수 있음 (그림 3 참고)
- 초기에는 3D 좌표 → 중간에는 64차원 feature → 후반에는 1024차원 등

2.1.2. 그래프 구성 $G = (V, E)$

$\mathcal{V}$ : 점들의 인덱스 집합 $\{1, 2, ..., n\}$
$\mathcal{E}$ : 간선들 (점들 사이의 연결 관계)
- $\mathcal{E} \subseteq \mathcal{V} \times \mathcal{V}$
- k-NN 그래프 사용 → 각 점마다 가까운 $k$ 개 점들과 연결
- Self-loop 포함 → 각 점은 자기 자신과도 연결

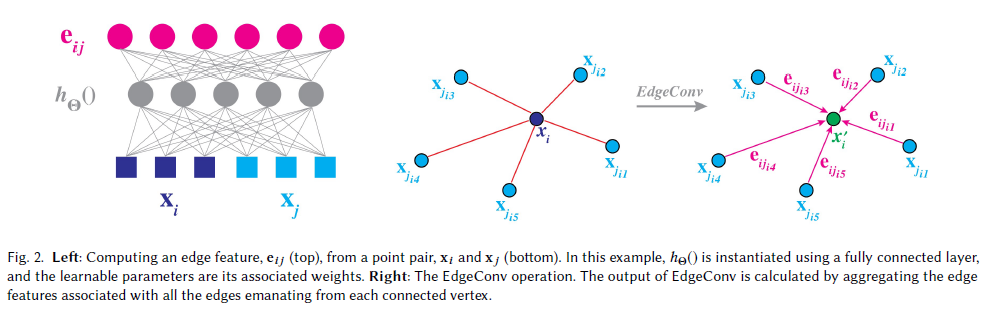
2.1.3. 엣지 특징 정의

두 점 $x_i, x_j$ 사이의 관계를 표현하기 위해 엣지 특징을 정의:

$e_{ij} = h_\Theta(x_i, x_j)$
- $h_\Theta$ : 비선형 함수 (예: MLP), 학습 가능한 파라미터 $\Theta$ 포함
- 각 엣지마다 하나의 피처를 생성함

2.1.4. EdgeConv 연산

하나의 점 $x_i$ 에 대해, 주변 이웃들과의 엣지 특징들을 모두 모은 다음, 합치기(aggregation) 함

$x'_i = □_j h_\Theta(x_i, x_j), \quad \text{for } (i,j) \in E$
- $□$ : 대칭적 집계 함수 (예: 합( $\sum$ ) 또는 최대값( $\text{max}$ ))
- 대칭적 집계 함수 특징은 element의 순서가 다르더라도 동일한 값을 산출함.
- 이렇게 해서, 새로운 피처 $x'_i$ 를 만듦

2.1.5. 이미지와의 유사성

마치 이미지의 중심 픽셀을 기준으로 주변 패치를 보는 것처럼,
포인트 클라우드에서 $x_i$ 는 중심점이고, 주변의 $x_j$ 는 패치처럼 다룸
그래서 이 연산을 "Edge Convolution"이라고 부름 (그래프 기반의 합성곱)

x'_{im} = \sum_{j: (i, j) \in \mathcal{E}} \theta_m \cdot x_j

$x_i, x_j$ : 피처 벡터. 여기서는 이미지 상의 픽셀 하나하나를 의미함 (예: RGB 값, 혹은 그 외의 피처들).
$\theta_m$ : 필터(커널)의 weight. m번째 필터를 의미.
$\mathcal{E}$ : $(i, j)$ 로 구성된 이웃 관계 (그래프의 edge들).
$x'_{im}$ : i번째 픽셀(또는 노드)에 대해 m번째 필터를 적용한 결과.

이미지의 각 픽셀을 노드로 생각합니다 ( $x_i$ }.
3x3 이웃 관계를 그래프의 edge로 연결합니다 → 즉, $(i, j) \in \mathcal{E}$
각 이웃 $x_j$ 에 대해 $\theta_m \cdot x_j$ 를 계산합니다 (필터 $m$ 과 내적)
이를 $\sum$ (혹은 $\text{max}$ 등)으로 모읍니다 → 이것이 aggregation

2.1.6. 다양한 $h$ 선택 예시들

이 부분이 핵심입니다! 어떤 함수 $h_\Theta(x_i, x_j)$ 를 쓰느냐에 따라 성능/특성이 달라집니다.

1) $h(x_i, x_j) = \theta_m \cdot x_j$ + 합(sum)

기존 CNN처럼 작동함
$\theta_m$ 은 필터 weight (벡터), 내적( $\cdot$ )은 convolution 역할
이건 정형 구조에서의 standard conv와 같음

2) $h(x_i, x_j) = h_\Theta(x_i)$

이웃 관계를 전혀 고려하지 않고 중심점의 정보만 사용
전역 구조(global structure)만 반영
PointNet이 이 방식을 씀

3) $h(x_i, x_j) = h_\Theta(x_j) \cdot g(u(x_i, x_j))$

$g$ : 가우시안 커널, $u$ : 거리 함수
이웃의 정보에 거리 기반 가중치를 곱함 (멀면 영향 적게)
로컬-글로벌 균형

4) $h(x_i, x_j) = h_\Theta(x_j - x_i)$

단순히 상대적 위치 차이만 학습
로컬 구조에 집중하지만, 전체 모양(global context)은 반영 못함

5) 이 논문이 제안하는 방식 (asymmetric):

h_\Theta(x_i, x_j) = \bar{h}_\Theta(x_i, x_j - x_i)

$x_i$ : 중심점 좌표 (global info)
$x_j - x_i$ : 중심 기준 이웃의 상대 위치 (local info)
이 둘을 조합 → 로컬+글로벌 정보 모두 사용

실제로는 이렇게 구현됨:

e'_{ijm} = \text{ReLU}(\theta_m \cdot (x_j - x_i) + \phi_m \cdot x_i)

MLP로 구현 가능
여기서 weight는 $\Theta = (\theta_1, . . . , \theta_M,\phi_1, . . . ,\phi_M)$ )이며, $\theta$ 는 local 정보인 $x_j - x_i$ 에 대한 weight 이고, $\phi$ 는 global 정보인 $x_i$ 에 대한 weight 임.
최종적으로 max pooling으로 aggregation 수행함:

x'_{im} = \max_{j: (i,j)\in E} e'_{ijm}

요약

개념	설명
Point Cloud	$n$ 개의 점과 각 점의 피처들
Graph $G$	점들 사이의 k-NN 기반 연결관계
Edge Feature $h(x_i, x_j)$	이웃과 중심의 관계를 표현하는 함수
Aggregation □	max 또는 sum 등을 통해 이웃 정보 집계
제안 방식	중심점과 상대 위치를 결합해 로컬+글로벌 특성 학습

2.2 Dynamic Graph Update

DGCNN은 각 레이어에서 동적으로 그래프를 업데이트합니다.
즉, 입력 시 고정된 그래프를 사용하지 않고, 각 레이어에서 새로 생성된 feature를 기반으로 k-NN 그래프를 다시 구성합니다.

핵심 아이디어

전통적인 Graph CNN은 입력 데이터 기반의 고정된 그래프를 사용.
DGCNN은 각 레이어에서 feature space 상에서 k개의 이웃을 다시 계산하여 그래프를 업데이트함.
이 구조 덕분에 네트워크가 학습을 통해 적절한 그래프를 동적으로 구성하게 됨.

효과

그래프가 매 레이어마다 새로 구성되므로 receptive field(수용 영역)가 점점 커짐.
최종적으로 point cloud 전체를 아우를 수 있을 정도로 넓어짐.
하지만 각 노드는 여전히 k개의 이웃만 참조하므로 그래프는 희소(sparse)하게 유지됨.

구현 방식

각 레이어에서:
- 현재 레이어의 feature들을 기반으로 쌍(pairwise) 거리 행렬을 계산.
- 각 포인트마다 가장 가까운 k개의 이웃을 선택.
- 이를 통해 새로운 그래프 $\mathcal{G}^{(l)} = (\mathcal{V}^{(l)}, \mathcal{E}^{(l)})$ 를 생성.

정리

이러한 동적 업데이트 방식은 DGCNN이 기존의 Graph CNN과 다른 주요한 특징.
네트워크가 데이터에 맞게 적절한 그래프 구조를 학습하며, 다양한 형태의 point cloud에 유연하게 대응 가능.

2.3 Properties

2.3.1. Permutation Invariance (순열 불변성)

EdgeConv의 중요한 성질 중 하나는 입력 포인트의 순서에 영향을 받지 않는다는 것입니다.

수식 설명

레이어의 출력은 다음과 같이 정의됩니다:

x'_i = \max_{j:(i,j) \in \mathcal{E}} h_\Theta(x_i, x_j)

$h_\Theta(x_i, x_j)$ : 포인트 $x_i$ 와 그 이웃 $x_j$ 사이의 관계를 나타내는 함수
$\max$ : 여러 이웃 포인트에 대한 값을 대칭적 방식으로 집계

순열 불변성(Permutation Invariance)이란?

포인트들의 순서를 바꿔도(예: $\{x_1, x_2, ..., x_n\} \rightarrow \{x_5, x_2, x_1, ...\}$ ) 결과가 변하지 않음
이유: $\max$ , $\text{mean}$ , $\sum$ 과 같은 symmetric aggregation function은 입력 순서에 무관하기 때문
전역적인 특징 집계(Global pooling)에서도 $max pooling$ 을 사용 → 이 역시 순열 불변성 보장

핵심 요점

포인트 순서에 상관없이 안정적인 특성 추출이 가능
이는 PointNet과 같은 기존 모델에서도 강조된 중요한 성질이며, DGCNN에서도 유지됨

2.3.2. Translation Invariance (이동 불변성)

EdgeConv 연산자는 부분적인 이동 불변성(partial translation invariance)을 가집니다. 이는 전체 좌표계가 이동해도 일부 특징은 유지된다는 의미입니다.

핵심 개념

논문에서 사용한 edge function은 다음과 같습니다:

e'_{ijm} = \theta_m \cdot (x_j - x_i) + \phi_m \cdot x_i

만약 포인트 클라우드가 어떤 벡터 $T$ 만큼 이동한다면:

x_j \rightarrow x_j + T,\quad x_i \rightarrow x_i + T

이때 연산 결과는:

e'_{ijm} = \theta_m \cdot ((x_j + T) - (x_i + T)) + \phi_m \cdot (x_i + T) \\ = \theta_m \cdot (x_j - x_i) + \phi_m \cdot (x_i + T)

해석

$x_j - x_i$ 부분은 이동 $T$ 에 무관 → 이동 불변성 유지
$\phi_m \cdot x_i$ 부분은 이동에 따라 변함 → 이동에 민감한(global shape 위치 정보) 요소

실험적 선택

만약 $\phi_m = 0$ 으로 설정한다면?

e'_{ijm} = \theta_m \cdot (x_j - x_i)

완전한 translation invariance 확보
하지만 이 경우, 모델은 patch들의 상대적 위치만 보고 전체 구조(형태, 방향)는 무시하게 됨

결론

$(x_j - x_i)$ : 로컬 패치의 상대적인 기하 정보
$x_i$ : 각 패치의 전역적인 위치 정보
두 정보를 함께 사용함으로써 모델은 로컬 + 글로벌 구조를 동시에 고려할 수 있음

2.4 Comparison to Existing Methods

DGCNN은 기존의 두 가지 주요 방식과 연관이 있습니다:

PointNet 계열
Graph CNN 계열

이들 각각은 DGCNN의 특정한 설정(special case)으로 볼 수 있습니다.

2.4.1. PointNet 계열

PointNet:
- DGCNN에서 k=1로 설정하면, 각 노드는 자기 자신만 이웃으로 가짐 ⇒ $\mathcal{E} = \phi$ (edge 없음).
- Edge function: $h_\Theta(x_i, x_j) = h_\Theta(x_i)$ → 로컬 구조를 무시하고, 전역 정보만 사용
PointNet++:
- 로컬 구조를 반영하기 위해 각 포인트 주변에서 PointNet을 적용.
- 그래프는 입력 포인트들의 유클리드 거리 기반으로 고정 구성.
- 각 레이어에서 Farthest Point Sampling (FPS)로 일부 포인트만 선택하고 나머지는 제거 → 그래프 크기 축소.
- Edge function: $h_\Theta(x_i, x_j) = h_\Theta(x_j)$
- Aggregation은 max pooling 사용.
- 한계: 그래프가 고정됨 → 동적인 정보 업데이트 불가능

2.4.2. Graph CNN 계열

DGCNN은 아래와 같은 기존 Graph CNN 방법들과도 관련 있습니다:
아래 방법들은 모두 고정된 그래프 위에서만 작동합니다.

MoNet ([Monti et al., 2017]):
- 로컬 "pseudo-coordinate system" $u(x_i, x_j)$ 을 정의하고, 이를 기반으로 가우시안 필터 적용:
  $x'_{im} = \sum_{j:(i,j)\in E} \theta_m \cdot \left( x_j \odot g_{w_n}(u(x_i, x_j)) \right)$
  - $\odot$ : elementwise (Hadamard) product
  - $g_{w_n}$ : 가우시안 커널 $\{w_1,w_2,...,w_N\}$
  - $\theta_m$ : 필터 계수 $\{\theta_1,\theta_2,...,\theta_M\}$
Atzmon et al. (2018):
- MoNet의 특수한 형태.
- 가우시안이 predefined 되어 있고, 학습 매개변수( $\{w_1,w_2,...,w_N\}$ )는 제거됨:
  $x'_{im} = \sum_{j \in V} (\theta_m \cdot x_j) \cdot g(u(x_i, x_j))$
  - 여기서 $u$ 는 유클리드 거리 기반

2.4.3. DGCNN의 차별점

기존 방법은 모두 고정된 그래프에서만 작동.
반면, DGCNN은 각 레이어마다 feature space에서 새롭게 그래프를 구성:
- 즉, 학습을 통해 "어떤 노드를 연결할 것인지"까지도 학습함
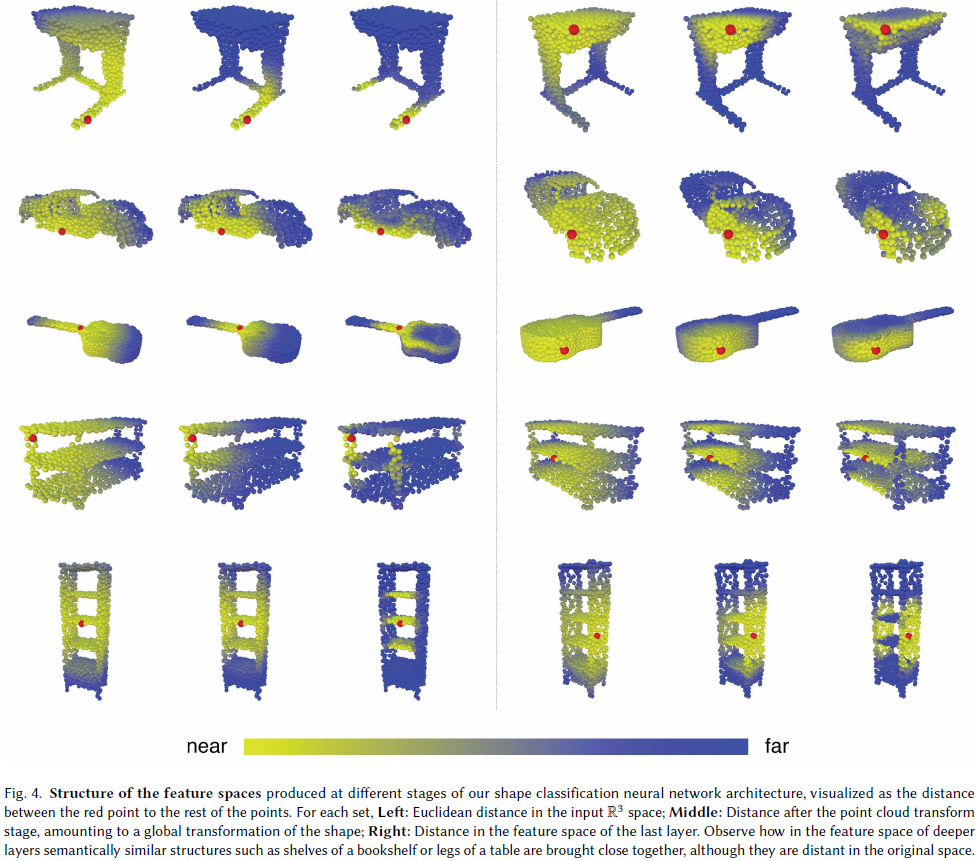
- 네트워크가 깊어질수록 feature space에서의 거리 = semantic distance
- → 학습된 임베딩 공간에서 멀리 있는 의미적 관계를 인식 가능 (그림. 4. 참고)

요약

방법	그래프 구성	Edge Function	Local/Global	그래프 고정 여부
PointNet	없음 (k=1)	$h(x_i)$	Global	고정
PointNet++	입력 좌표 기반	$h(x_j)$	Local + 일부 Global	고정
MoNet	주어진 G + 가우시안	$x_j \odot g(u(x_i, x_j))$	Local	고정
DGCNN	Feature space에서 학습	$\theta \cdot (x_j - x_i) + \phi \cdot x_i$	Local + Global	동적 그래프

3. 결과 (Results)

3.1 Model Complexity

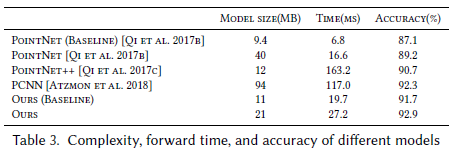
요약 정리

실험 기반: ModelNet40 데이터셋을 활용한 분류 실험을 통해 모델 복잡도 비교.
지표: 모델 복잡도는 다음 세 가지로 평가됨:
1. 모델 파라미터 수
2. 계산 복잡도 (Forward pass 시간)
3. 분류 정확도

주요 결과

정적 k-NN 그래프를 사용하는 기본 DGCNN 모델은:
- PointNet++보다 1.0% 높은 정확도
- 계산 속도는 7배 빠름
동적 그래프 업데이트를 포함한 고급 모델은:
- PointNet++보다 2.2%, PCNN보다 0.6% 높은 정확도
- 더 높은 효율성 제공
모든 실험은 1024 포인트를 사용해 수행됨.

3.2 More Experiments on ModelNet40

실험 목적

ModelNet40 데이터셋을 사용하여 다양한 설정에서 DGCNN의 성능을 분석함:

거리 측정 방식
edge feature로 xi − xj 사용 여부
포인트 수 증가
k-NN 개수 변화
테스트 시 포인트 밀도 변화에 대한 모델의 강건성

주요 실험 결과 요약

Patch 중앙화 (Centralization)
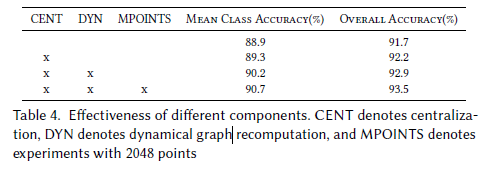
- $x_i$ 와 $x_j$ 의 결합 대신 $x_i$ 와 $(x_i − x_j)$ 를 결합 → 약 0.5% 정확도 증가 (Table 4.의 CENT 참고)
Dynamic Graph Recalculation (동적 그래프 재구성)
- 각 레이어에서 그래프를 다시 계산 → 약 0.7% 정확도 증가 (Table 4.의 DYN 참고)
- Figure 4를 통해 의미 있는 feature 추출 가능성 시사
포인트 수 증가
- 더 많은 포인트 사용 → 약 0.6% 정확도 향상 (Table 4.의 MPOINTS 참고)
k-NN 이웃 개수 변화
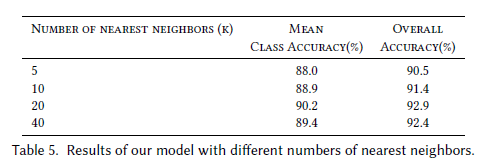
- 실험 결과, k가 너무 커지면 성능 저하 (Table 5 참고)
- 이유: 유클리드 거리로는 지오데식(geodesic) 거리 근사가 어려워 patch 기하구조 손상
- Euclidean거리는 두 점 사이의 최단 직선거리를 뜻하지만, 지오데식 거리는 구조를 따라간 최단거리를 뜻합니다.
포인트 밀도 감소에 대한 강건성 실험
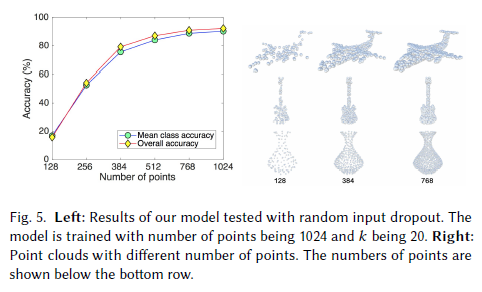
- 테스트 시 무작위로 포인트 제거
- 512개 이상 유지 시 견고 (Figure 5 참조), 그러나 그 이하로는 성능 급감

3.3 Intra-cloud 거리 분석

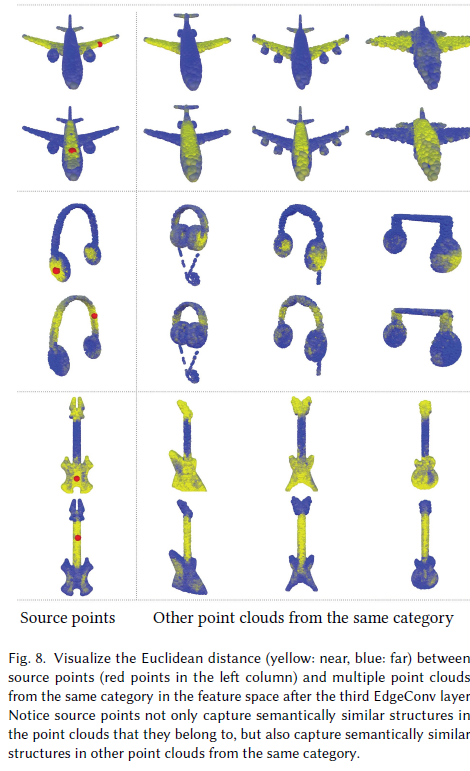
DGCNN 모델에서 추출된 feature를 활용해, 서로 다른 point cloud 간의 관계를 탐색합니다.
Figure 8에서 보이듯, 한 source point cloud에서 빨간 점 하나를 선택하고,
같은 카테고리에 속하는 다른 point cloud의 각 점들과 feature 공간에서의 거리를 계산합니다.

주요 발견

비록 점들이 서로 다른 객체에서 왔지만, 의미적으로 유사한 부분이라면 feature 공간상에서 서로 가까운 거리에 위치합니다.
- 예: 비행기의 날개, 의자의 다리 등
이는 DGCNN이 의미 기반의 표현(semantic representation)을 효과적으로 학습했다는 증거입니다.

실험 조건

사용한 feature는 세 번째 레이어 이후의 feature입니다.
해당 레이어에서는 고차원의 의미적 정보를 포함한 표현이 형성됩니다.

4. 토론 (DISCUSSION)

이번 논문에서는 포인트 클라우드(Point Cloud) 상에서 학습을 수행하기 위한 새로운 연산자(operator)를 제안하고, 이를 다양한 작업에 적용해 성능을 입증하였습니다.
모델 실험 결과, 딥러닝 기법을 도입한 이후에도 지역적인 기하 정보(local geometric features)는 3D 인식 작업에서 여전히 매우 중요한 요소임을 보여줍니다.

모델 활용과 확장 가능성

제안한 아키텍처는 기존의 포인트 클라우드 기반 그래픽스, 머신러닝, 비전 파이프라인에 쉽게 통합될 수 있습니다.
실험 결과는 다음과 같은 향후 연구 방향을 시사합니다:

향후 개선 및 확장 아이디어

효율성과 확장성 향상
- 현재는 k-NN을 위해 모든 쌍(pairwise)의 거리를 계산하고 있는데,
  빠른 자료구조(fast data structures)를 사용하면 속도와 메모리 측면에서 개선 가능함.
고차 관계(high-order relationships)
- 현재는 점을 쌍(pairwise)으로만 고려하지만,
  더 큰 튜플(예: 세 점 이상)을 고려한 관계 확장이 가능함.
비공유(non-shared) 트랜스포머 설계
- 각 로컬 패치마다 다르게 작동하는 유연한 트랜스포머 네트워크를 설계할 수 있음.

본질적(intrinsic) 특성의 중요성

실험에서는 좌표 기반의 외재적 정보(extrinsic features) 못지않게
내재적 특성(intrinsic features) 역시 중요하다는 사실을 보여줌.
(여기서 $x_j-x_i$ , dynamic graph 및 local 정보들이 내재적 특성을 포함합니다.)
향후에는 이 두 가지 특성의 균형을 잡기 위한 이론적·실용적 프레임워크 개발이 필요함.

적용 분야의 확장

본 연구의 기법은 단순한 3D 지오메트리 외에도 다음과 같은 추상적 데이터 도메인에도 적용 가능함:
- 문서 검색(Document Retrieval)
- 이미지 처리(Image Processing)
이러한 실험을 통해 추상 데이터 처리에서의 기하학 정보의 역할에 대한 통찰을 얻을 수 있을 것임.

Bean

AI developer

이전 포스트

Shape As Points (SAP) 리뷰

다음 포스트