신경망의 표현력, 왜 '비선형'이 핵심인가?
왜 선형 함수만으로는 부족할까?
신경망을 아무리 깊게 쌓더라도, 각 층이 선형 변환만 한다면 전체 네트워크는 여전히 하나의 선형 함수에 불과합니다.
수식으로 보면,
- 첫 번째 층:
f₁(x) = A₁x - 두 번째 층:
f₂(f₁(x)) = A₂A₁x - 결국:
f(x) = Ax(하나의 선형 변환)
즉, 여러 층을 쌓아도 선형성만 있다면 표현력은 하나의 선형 모델과 다르지 않습니다.
이로 인해 다음과 같은 한계가 생깁니다:
- 복잡한 경계를 가진 문제(예: XOR)를 해결할 수 없음
- 입력-출력 관계를 정교하게 모델링하지 못함
비선형성은 어떻게 표현력을 향상시킬까?
여기에 활성화 함수 (ReLU, sigmoid, tanh 등) 같은 비선형 요소를 삽입하면 상황이 완전히 달라집니다.
각 층이 비선형 변환을 포함하게 되면, 신경망은 단순한 선형 조합이 아닌 복잡한 함수 조합을 만들 수 있습니다.
이로 인해 네트워크는 다음과 같은 능력을 가집니다:
- 입력 공간을 “구부리기” 또는 “잘라내기”
- 비선형 경계 생성
- 고차원 공간에서 복잡한 패턴 인식
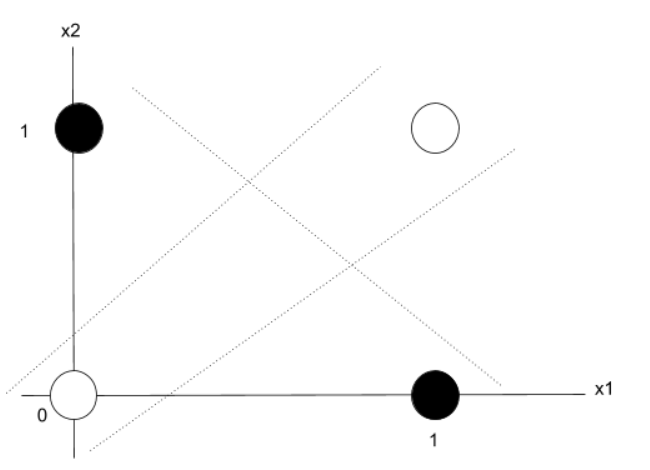
예제로 보는 비선형성의 힘: XOR 문제
XOR 입력/출력
| x₁ | x₂ | y (x₁ ⊕ x₂) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
이 문제는 선형 모델로는 절대 해결할 수 없는 고전적인 예제입니다.
👉 Python 구현 코드 (XOR 문제)
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neural_network import MLPClassifier
# XOR 데이터 생성
X = np.array([[0,0], [0,1], [1,0], [1,1]])
y = np.array([0, 1, 1, 0])
# 모델: 은닉층 1개 (2뉴런), 비선형 활성화 함수 (ReLU)
model = MLPClassifier(hidden_layer_sizes=(2,), activation='relu', max_iter=1000)
model.fit(X, y)
# 예측 결과 확인
print("예측 결과:", model.predict(X))
# 시각화
h = 0.01
xx, yy = np.meshgrid(np.arange(-0.1, 1.1, h), np.arange(-0.1, 1.1, h))
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap=plt.cm.coolwarm, alpha=0.6)
plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k', cmap=plt.cm.coolwarm, s=100)
plt.title("XOR Problem - Nonlinear Classification with Hidden Layer")
plt.xlabel("x1")
plt.ylabel("x2")
plt.grid(True)
plt.show()결과 해석
- 네트워크는 비선형 활성화 함수 덕분에 선형으로 분리 불가능한 XOR 문제를 해결합니다.
- 은닉층이 입력 공간을 비틀어 새로운 표현 공간으로 변형 → 비선형 결정 경계를 만들어냄
유니버설 근사 정리란?
"충분히 많은 뉴런과 비선형성을 갖춘 신경망은 모든 연속 함수를 근사할 수 있다."
이 정리는 왜 비선형성이 중요한지를 이론적으로 뒷받침합니다.
→ 만약 비선형성이 없다면, 아무리 층을 쌓아도 네트워크는 고작 하나의 선형 모델일 뿐입니다.