
INTRO
1) 오늘은 시계열 데이터 예측을 해보려고 한다.
2) RNN에 대한 기본적인 개념과 지식은 어느 정도 알고 있다고 가정하고 시작하겠다.
3) 성능은 장담하지 않는다. (시계열 데이터 전처리 및 도메인 지식 부재)
- Pytorch의 Basic Flow를 익히는 것이 주목적이기 때문
- Kaggle에 Bitcoin Historical Data 라는 데이터셋을 사용한다.
- EDA, PREPROCESSING 모두 생략 -> BASIC FLOW에 익히는 것이 목적
- X columns:Open, High, Low
- y column: Close
- 361370의 Row가 존재하는 데, 이 중 1%만 사용
: 좀 오래 걸리기 때문 (원한다면 100% 써서 사용해보자.)
- [가장 중요] 데이터의 Shape 추적은 반드시 하자.
- 혹시라도 잘못된 부분이 있다면 꼭 알려줬으면 한다.
Code
- 실습코드 - Colab에서뿐만 아니라, M1에서도 잘 돌아간다.
순서
: Kaggle API -> Import -> Data -> Dataset -> DataLoader -> Model -> Loss Function and Optimizer -> train_one_epoch() and valid_one_epoch() -> run_train()
00 Kaggle API
: Colab Cell에서 다음과 같이 입력하여 Kaggle Dataset을 한 번에 다운로드할 수 있다.
- 'KAGGLE_USERNAME', 'KAGGLE_KEY'의 경우, Kaggle에서 'Your Profile' -> 'Account' 탭 -> 'API'에서 얻을 수 있다.

import os
# os.environ을 이용하여 Kaggle API Username, Key 세팅하기
os.environ['KAGGLE_USERNAME'] = ############
os.environ['KAGGLE_KEY'] = ############
# Linux 명령어로 Kaggle API를 이용하여 데이터셋 다운로드하기 (!kaggle ~)
!kaggle datasets download -d mczielinski/bitcoin-historical-data
# Linux 명령어로 압축 해제하기
!unzip '*.zip'압축 해제가 끝났다면, 어떤 파일들이 있는지 살펴보자.
!ls
01 IMPORT
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import torch
import torch.nn as nn
from torch.utils.data import Dataset, DataLoader1) import torch.nn as nn
: nn을 이용해서 nn.Module을 상속받아서 다음 예시처럼 Model을 빌드한다. 그래서 필요하다.
class Model(nn.Module):
def __init__(self, input_dim = 8, output_dim = 1):
super().__init__()
self.fc1 = nn.Linear()
...2) from torch.utils.data import Dataset, DataLoader
: Dataset과 DataLoader는 데이터를 배치 단위로 학습할 데이터(x)와 정답 데이터(y)를 묶어서 뱉어주는 역할을 한다.
02 DATA
: Kaggle에 Bitcoin Historical Data 라는 데이터셋을 사용한다.
- EDA, PREPROCESSING 모두 생략 -> BASIC FLOW에 익히는 것이 목적
- 사용할 컬럼은 다음과 같다.
- Open, High, Low : 학습할 데이터 컬럼
- Close : label 컬럼
- Weighted Price 컬럼을 label 컬럼으로 사용해도 무관하다.
- 필자는 그냥 Close로 선택하고 문제정의한 것이다.
- 361370의 Row가 존재하는 데, 이 중 1%만 사용
- 사유: 좀 오래 걸리기 때문 (원한다면 모두 사용해도 된다.)
base_path = '/content/bitstampUSD_1-min_data_2012-01-01_to_2021-03-31.csv'
df = pd.read_csv(base_path)
df = df[df.Open.notnull()].reset_index(drop = True)
# 결측치 제거 및 index 초기화
num = int(df.shape[0] * .01)
print(num)
df = df[:num] # 1%의 데이터만 사용!
print(df.shape)
df.head()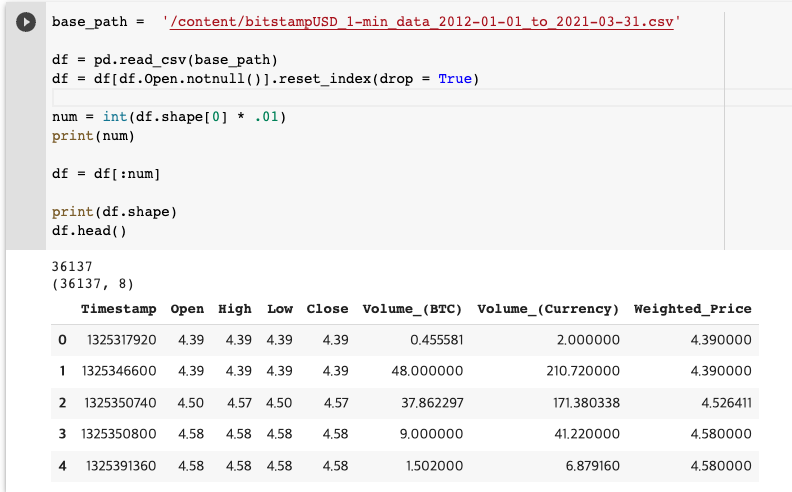
03 Dataset
: Dataset을 상속받아서 MyDataset 클래스를 만들어준다.
sl = 12
class MyDataset(Dataset):
def __init__(self, df = df, days = sl):
self.days = days # RNNModel에서 Sequence Length가 된다.
# x
self.x = df.iloc[:, 1:4].values # Open, High, Low
self.x = self.x / np.max(self.x) # Scaling
# y
self.y = df.iloc[:, 4:5].values # Close
self.y = self.y / np.max(self.y) # Scaling
def __len__(self):
# 전체 길이 정보를 반환.
return self.x.shape[0] - self.days
def __getitem__(self, index):
# index를 통해서 row 하나를 특정.
x = self.x[index: index + self.days]
# index ~ index + 3 -> x's Shape: [12, 3]
y = self.y[index + self.days]
# index + 3 -> y's Shape: [1]
return torch.tensor(x, dtype = torch.float), torch.tensor(y, dtype = torch.float)
# Shape: [12, 3] Shape: [1]- def __init__(self)
- 생성자 함수에서는 전체 데이터셋에서의 X,Y를 선언
- self.x = df.iloc[:, 1:4].values
- 'Open' ~ 'Low'까지 인덱싱
- .values 붙여서 pandas DataFrame에서 numpy array로 변환
- def __len__(self)
- 여기서는 전체 데이터의 길이 정보를 반환한다.
- def __getitem__(self)
- 여기서는 'index'로 인덱싱하여, row 하나를 특정한다.
- 이게 잘 안 와닿으면, KFold 생각하면 될 것이다.
## 다른 데서 코드 가져옴 for fold, ( _, val_) in enumerate(skf.split(X=df, y=df['target'])): df.loc[val_ , "kfold"] = int(fold) # _, val_ : index 넘버 - x = self.x[index] 이런 식으로 인덱싱을 한다.
- self.x는 특정 컬럼에 대한 전체 Row의 데이터.
- 여기서 x, y는 index로 특정된 row 한 줄에서의 x, y이다.
- x는 [12, 3] Shape의 행렬로 존재 (row 1개의 x)
- y는 1개의 target 숫자로 이루어져있다. Shape은 [1]
- 이게 잘 안 와닿으면, KFold 생각하면 될 것이다.
- 우리는 토치의 민족이기 때문에 x, y를 토치 텐서로 반환하여 반환해준다.
return torch.tensor(x, dtype = torch.float), torch.tensor(y, dtype = torch.float)
- 여기서는 'index'로 인덱싱하여, row 하나를 특정한다.
04 prepare_loaders: Dataset -> DataLoader
: 여기서는 학습에 사용할 데이터와 성능 검증에 필요한 데이터로 쪼개준다. 그리고 각 데이터에 대해서 배치 단위로 뱉어줄 수 있도록 DataLoader 객체를 각각 만들어준다. 이 과정을 prepare_loaders() 함수에 담았다.
def prepare_loaders(df = df, index_num = int(df.shape[0] * .7), bs = 128 * 2):
# train, valid split (7:3 Split)
train = df[:index_num].reset_index(drop = True)
valid = df[index_num:].reset_index(drop = True)
# train_ds, valid_ds MyDataset(Dataset)
train_ds = MyDataset(df = train)
valid_ds = MyDataset(df = valid)
# train_loader, valid_loader를 만들어준다.
# 시계열 데이터이기 때문에 Shuffle 에 대해서는 False로 주었다.
train_loader = DataLoader(train_ds, shuffle = False, batch_size = bs)
valid_loader = DataLoader(valid_ds, shuffle = False, batch_size = bs)
return train_loader, valid_loadertrain_loader에서 나오는 배치의 Shape을 확인해보자.
: Data의 Shape 추적이 가장 중요하다. 그래서 여기서도 확인해볼 필요가 있다. 아마 x에 해당하는 부분의 Shape은 [256, 12, 3], y에 해당하는 부분의 Shape은 [256, 1] 으로 나올 것이다.
## train_loader가 뱉는 배치 크기 확인해보자
data = next(iter(train_loader))
data[0].shape, data[1].shape
05 device
: torch.tensor를 비롯해서 train_loader, valid_loader에서 나오는 배치들과 Model의 layer들을 모두 GPU로 보내기 위한 코드이다. M1, Colab에서 적용할 수 있는 코드이며, '지금 GPU 쓸 수 있니? 없니?' 라고 확인 후, if else 조건문을 통해 GPU로 보내는 코드이다.
# Colab
# device = torch.device("cuda:0") if torch.cuda.is_available() else torch.device("cpu")
# M1 버전
device = torch.device("mps") if torch.backends.mps.is_available() else torch.device("cpu")
device06 Model
: nn.Module을 상속받아서 Model 클래스를 빌드한다.
: RNN 계열의
class RNNModel(nn.Module):
def __init__(self,
input_size = 3, # open, high, low
hidden_size = 100,
num_layers= 3,
sequence_length = sl, # sl = 12
device = device
):
super().__init__()
self.num_layers = num_layers
self.sequence_length = sequence_length
self.hidden_size = hidden_size
self.device = device
# RNN 레이어
# https://pytorch.org/docs/stable/generated/torch.nn.RNN.html
self.rnn = nn.RNN(input_size = input_size,
hidden_size = hidden_size,
num_layers = num_layers,
batch_first = True,
bidirectional = False)
# input(=x)'s shape: [bs, sl, input_size]
# input_h0 = [num_layers, bs, hidden_size]
# output(=y)'s shape: [bs, sl, hidden_size]
# output_h = [num_layers, bs, hidden_size]
# [bs, sl, hidden_size] -> [bs, sl * hidden_size]
# 1) 3차원 -> 2차원
k = self.sequence_length * self.hidden_size
# 2) Use output's Last Sequence Length
# k = 1 * self.hidden_size
# Fully Connected Layer
self.seq = nn.Sequential(
nn.Linear(k, 256),
nn.LeakyReLU(),
nn.Linear(256, 1)
# [bs, k] -> [bs, 256] -> [bs, 1]
)
def forward(self, x):
# x: [bs, sl, input_size]
bs = x.shape[0]
h0 = torch.zeros(self.num_layers, bs, self.hidden_size).to(self.device)
# h0: [num_layers, bs, hidden_size]
output, h_n = self.rnn(x, h0)
# output's shape: [bs, sl, hidden_size]
# h_n = [num_layers, bs, hidden_size]
# 1) 3차원 -> 2차원
output = output.reshape(bs, -1)
# [bs, sl, hidden_size] -> [bs, sl * hidden_size]
# 2) Use output's Last Sequence Length
# output = output[:, -1] # [bs, hidden_size]
# [bs, k] -> [bs, 256] ->[bs, 1]
y_pred = self.seq(output)
# y_pred: [bs, 1]
return y_pred
model = RNNModel().to(device) # GPU로 보내준다.- 데이터가 배치 단위로 들어온다.
- x가 배치단위로 묶여서 [bs, 12, 3] Shape으로 들어온다. (bs: 배치단위크기)
- model의 최종값(y_pred)는 Predicted 값이며, Shape은 [bs, 1]로 나온다.
- y가 배치단위로 묶여서 [bs, 1] Shape으로 나타나는데, 이 때의 Shape과 동일
- def __init__(self) 에서는 'Frame만 선언'해준다고 생각하면 된다.
- def forward(self, x) 에서는 '실질적으로 위에서 선언한 Frame들을 함수형태로 넣어주며 엮어주는 곳'이라고 생각한 된다.
- Shape 추적을 하면서 코드를 짜야한다. 그래야 오류가 안 나고 어떤 일이 일어나는 지 상세하게 알 수 있다.
07 Loss Function and Optimizer
: Loss Function과 Optimizer를 선언한다.
- MSELoss
- Adam
# loss_fn도 to(device)가 가능하다. (= GPU로 보내줄 수 있다.)
loss_fn = nn.MSELoss().to(device)
# optimizer는 to(device)가 불가능하다. (= GPU로 보내줄 수 없다.)
optimizer = torch.optim.Adam(model.parameters()) # lr = 1e-308 train_one_epoch()
: model이 한 epoch를 도는 동안, model이 학습되는 과정과 train_epoch_loss(=epoch당 평균 train loss)를 return 시키는 함수이다.
- model이 학습을 진행 (Back-Prop)
- train 데이터 -> train_loader
def train_one_epoch(model = model,
dataloader = train_loader,
loss_fn = loss_fn,
optimizer = optimizer,
device = device):
# model을 학습시키겠다고 선언
model.train()
train_loss = 0
for data in dataloader:
# train_loader = [([bs, 12, 3], [bs, 1]), ([bs, 12, 3], [bs, 1]), .... ]
x = data[0].to(device) # [bs, 12, 3] # GPU로 보내준다.
y = data[1].to(device) # [bs, 1] # GPU로 보내준다.
y_pred = model(x) # [bs, 1] # model을 통해 예측한 값
loss = loss_fn(y_pred, y) # MSE Loss
optimizer.zero_grad() # Gradient 초기화
loss.backward() # 역전파할 Gradient 구함
optimizer.step() # 역전파할 Gradient 토대로 Weight 업데이트
train_loss += loss.item()
train_epoch_loss = train_loss / len(dataloader) # epoch 당 train loss 평균값
return train_epoch_loss09 valid_one_epoch()
: model이 한 epoch를 도는 동안, valid_epoch_loss(=epoch당 평균 valid loss)를 return 시키는 함수이다.
- 여기서는 model이 학습되지 않는다.
- 오직 성능 평가만 한다.
- valid 데이터 -> valid_loader
- 실제값들과 예측값들을 시각화해서 볼 수 있도록 list에 담을 예정
# @torch.no_grad() : 데코레이터 형태의 'model을 학습 시키지 않겠다는 필수 의지 표명 2'
# --> 근데 함수형일 때 쓸 수 있는 것으로 알고 있다.
# --> model을 학습 시키지 않겠다는 필수 의지 표명 1과 2 중 하나만 써도 무방하다.
@torch.no_grad()
def valid_one_epoch(model = model,
dataloader = valid_loader,
loss_fn = loss_fn,
device = device):
# 여기서는 optimizer가 필요없다. 학습을 하지 않기 때문
# model을 학습 안 시키겠다고 선언
model.eval()
# 예측값들과 실제값들을 담을 빈 리스트를 선언
# 예측값과 실제값을 볼 수 있는 시각화 용도
preds = []
trues = []
valid_loss = 0
# model을 학습 시키지 않겠다는 필수 의지 표명 1
with torch.no_grad():
for data in dataloader:
# valid_loader = [([bs, 12, 3], [bs, 1]), ([bs, 12, 3], [bs, 1]), .... ]
x = data[0].to(device) # [bs, 12, 3] # GPU로 보내준다.
y = data[1].to(device) # [bs, 1] # GPU로 보내준다.
y_pred = model(x) # [bs, 1] # model을 통해 예측한 값
loss = loss_fn(y_pred, y) # MSE Loss - 성능평가
valid_loss += loss.item()
# 예측값들 줍줍
preds.append(y_pred)
# 실제값들 줍줍
trues.append(y)
valid_epoch_loss = valid_loss / len(dataloader) # epoch 당 valid loss 평균값
# 줍줍한 예측값들을 concat
preds_cat = torch.cat(preds, dim = 0)
# 줍줍한 실제값들을 concat
trues_cat = torch.cat(trues, dim = 0)
return valid_epoch_loss, trues_cat, preds_cat10 run_train()
: 여기서는 전반적인 train 과정을 담았다.
- train_one_epoch() / valid_one_epoch()
- 시각화를 위한 epoch당 평균 train_loss, valid_loss 담기
- monitoring: 특정주기마다 loss들 체크
- Lowest Loss가 갱신될 때, model 저장
- 오버피팅 방지를 위한 early_stop
- 그 외 다른 설명은 주석으로 달아두었다.
def run_train(model = model,
loss_fn = loss_fn,
optimizer = optimizer,
train_loader = train_loader,
valid_loader = valid_loader,
device = device):
n_epochs = 200
print_iter =20
best_model = None
early_stop = 30
lowest_loss, lowest_epoch = np.inf, np.inf
train_hs, valid_hs = [], []
result = dict()
for epoch in range(n_epochs):
train_loss = train_one_epoch(model = model, dataloader = train_loader, loss_fn = loss_fn, optimizer=optimizer, device = device)
valid_loss, trues_cat, preds_cat = valid_one_epoch(model = model, dataloader = valid_loader, loss_fn = loss_fn, device = device)
# rues_cat, preds_cat은 각각 한 에폭에서 예측값, 실제값들을 담은 리스트.
# Valid 데이터 대상
# 매 epoch 마다 train_loss, valid_loss를 줍줍
train_hs.append(train_loss)
valid_hs.append(valid_loss)
# monitoring: print_iter 주기만큼 print문을 찍어줍니다.
if (epoch + 1) % print_iter == 0:
print("Epoch:%d, train_loss=%.3e, valid_loss=%.3e, lowest_loss=%.3e" % (epoch+1,train_loss, valid_loss, lowest_loss))
# lowest_loss 갱신
if valid_loss < lowest_loss:
lowest_loss = valid_loss
lowest_epoch = epoch
# model save
torch.save(model.state_dict(), "./model_rnn.pth")
else:
if early_stop >0 and lowest_epoch + early_stop < epoch + 1:
print("삽질 중")
break
print("The Best Validation Loss=%.3e at %d Epoch" % (lowest_loss, lowest_epoch))
# model load
model.load_state_dict(torch.load("./model_rnn.pth"))
# result 라는 딕셔너리를 생성해서 train_hs, valid_hs 를 담아줍니다.
result["Train Loss"] = train_hs
result["Valid Loss"] = valid_hs
# trues_cat(y값들), preds_cat(y_pred값들): 마지막 epoch에서의 값들만 줍줍하여, result에 넣는다.
# 실제값들과 예측값을 시각화하여 보기 위함.
# 마지막 에포크의 예측값들과 실제값들이 담길 것
result["Trues"] = trues_cat
result["Preds"] = preds_cat
return model, result11 train 시작!
: 다음 코드로 학습 시작!
model, result = run_train()
- "삽질 중"이라는 문구가 떴다면, early stop이 적용된 것을 알 수 있다.
- 23 Epoch에서 최저의 Valid Loss가 발생하였고, 23 Epoch부터 53 Epoch까지의 Loss 중 23 Epoch에서의 Loss보다 작은 Loss가 없어서(=Lowest Loss 갱신이 안 되서) "삽질 중" 문구를 print하고 break 되서 train이 종료된 것이다.
12 시각화 - train_loss, valid_loss
1) train loss, valid loss 추이 비교
## Visualization: Train Loss, Valid Loss
plot_from = 0
plt.figure(figsize=(20, 10))
plt.title("Train/Valid Loss History", fontsize = 20)
plt.plot(
range(0, len(result['Train Loss'][plot_from:])),
result['Train Loss'][plot_from:],
label = 'Train Loss'
)
plt.plot(
range(0, len(result['Valid Loss'][plot_from:])),
result['Valid Loss'][plot_from:],
label = 'Valid Loss'
)
plt.legend()
# plt.yscale('log')
plt.grid(True)
plt.show()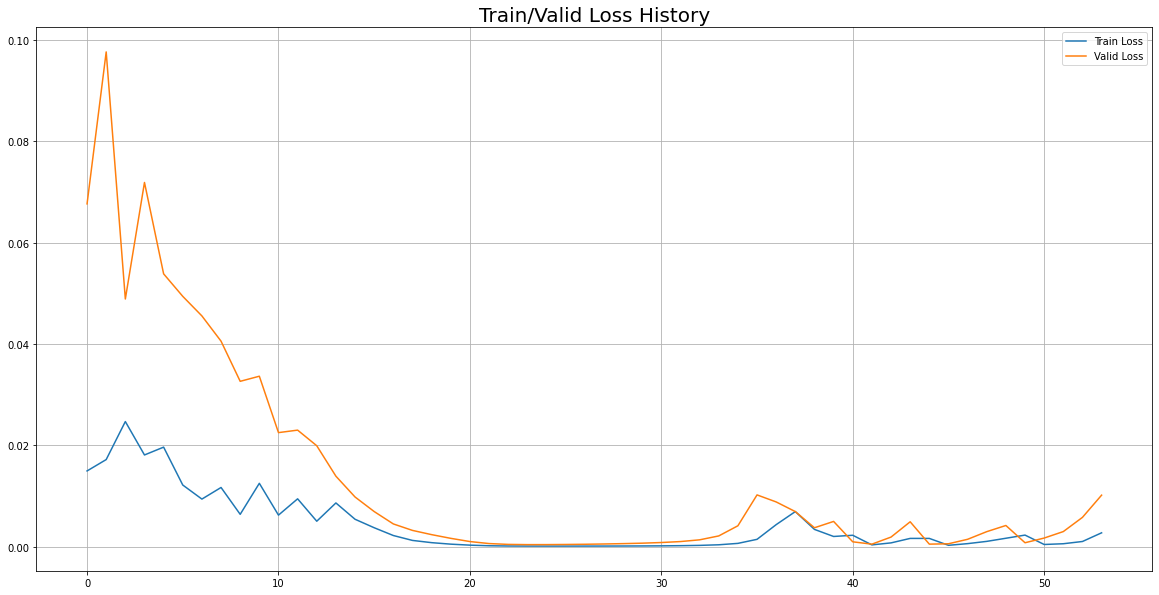
2) Valid 데이테에 대한 실제값과 예측값을 비교
## Visualization: True Values and Predicted Values
plot_from = 0
plt.figure(figsize=(20, 10))
plt.title("Trues, Preds History", fontsize = 20)
plt.plot(
range(0, len(result['Trues'].detach().cpu().numpy()[plot_from:])), # 마지막 에포크에서의 실제값들입니다.
result['Trues'].detach().cpu().numpy()[plot_from:],
label = 'Trues'
)
plt.plot(
range(0, len(result['Preds'].detach().cpu().numpy()[plot_from:])), # 마지막 에포크에서의 예측값들입니다.
result['Preds'].detach().cpu().numpy()[plot_from:],
label = 'Preds'
)
plt.legend()
# plt.yscale('log')
plt.grid(True)
plt.show()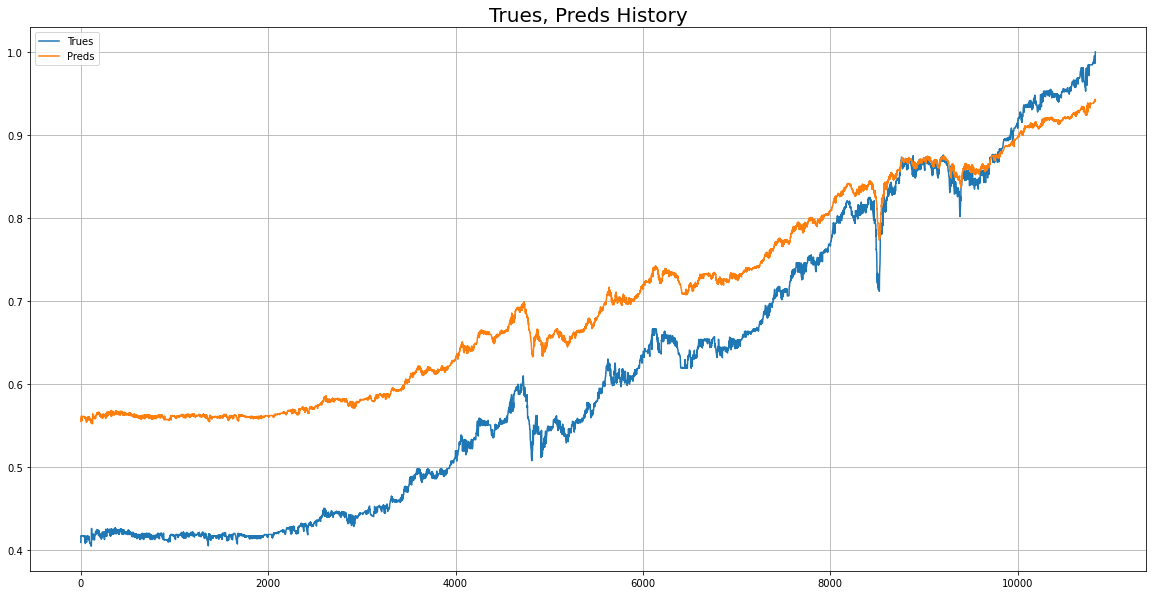
성능은 장담하지 못 한다.
보면 알겠지만, 성능은 장담하지 못 한다. 필자의 경우, 시계열 예측에 필요한 전처리 방법 혹은 비트코인 주가 예측에 필요한 도메인 지식 또한 없다.
03 RNN and his firends PART 01이 끝났다.
- 실습코드는 M1에서도 잘 돌아간다.
- 이후 PART 02에서는 다른 RNN 계열 모델과 다른 방법으로 예측하는 것을 보여주도록 하겠다.
