Ch4-1. Divide and Conquer I

이동윤·2025년 3월 23일
알고리즘
0

Algorithm

목록 보기
4/11

지금까지 우린 Insertion Sort에 대해서 공부했다.
삽입정렬만으로 모든 Sorting문제들을 해결하면 얼마나 좋을까?
하지만 애석하게도 우리가 공부했던 삽입정렬을 쓸 일은 생각보다 많지 않을 것이다🥲

세상에는 그것보다 더 효율적인 정렬 방법이 너무나도 많다.
그 중에서 우리는 오늘 Divide & Conquer 방식을 사용한 병합 정렬에 대해 알아볼 것이다.

사람은 하고싶은것만 하고 살 수 없다.

Divide & Conquer 이란?

필자는 이 부분을 공부할때마다 이 노래를 한번 듣고 간다.
듣기만해도 분할정복정복자가 된 것 같은 느낌이다.


일단 분할 & 정복이 무엇인지부터 알아보자.

1. Divide(분할)

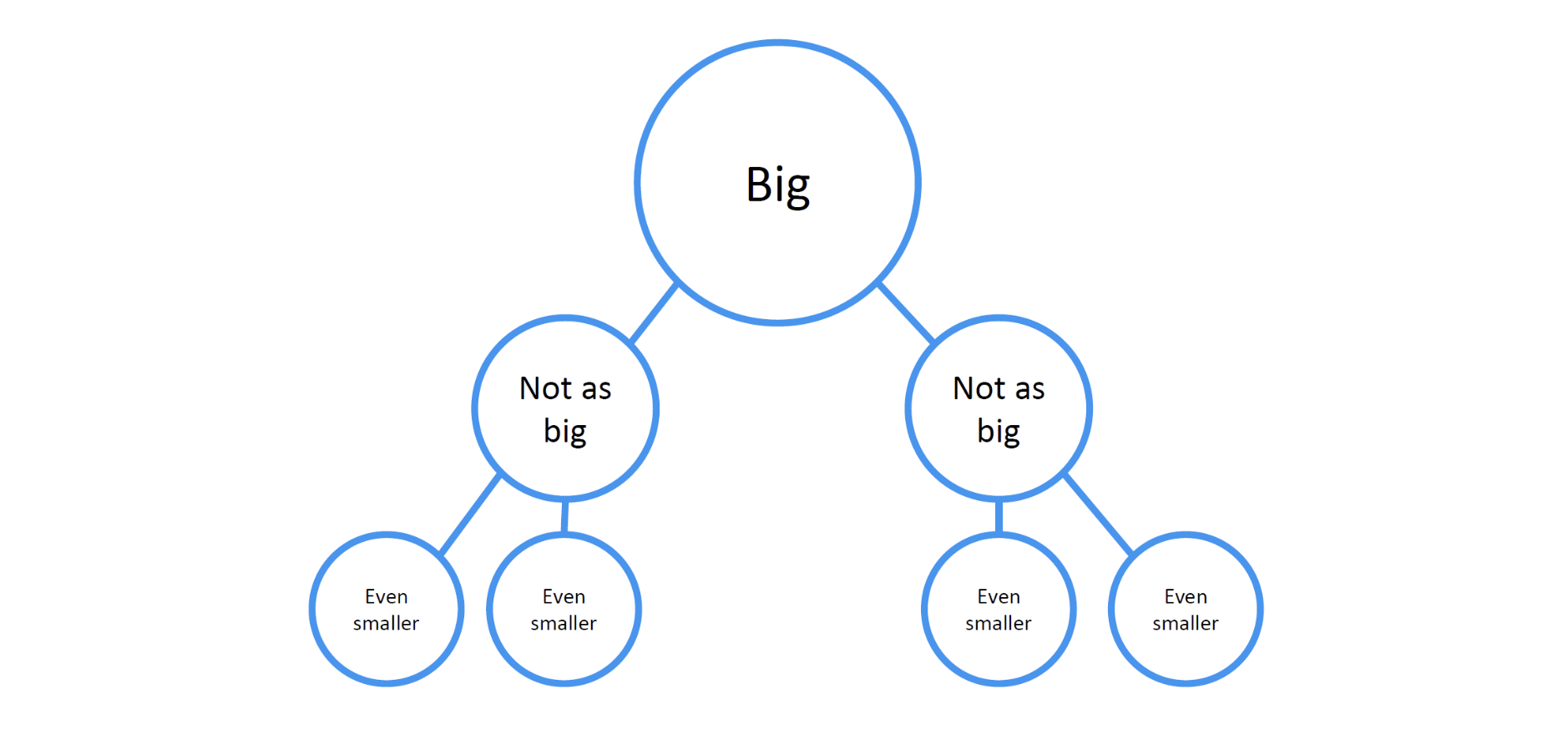
“큰 문제(Big)를 더 작은 문제(Not as big)로 쪼개는 과정”.

-> 정렬 알고리즘에 적용하면, 정렬해야 할 전체 배열을 둘(또는 여러 부분)로 나누는 식

예시: 병합 정렬(Merge Sort)에서는 리스트를 정확히 절반씩 분할.
예시: 퀵 정렬(Quick Sort)에서는 피벗을 기준으로 작은 그룹, 큰 그룹으로 나누어 정렬.

👍 분할의 이점

  1. 복잡한 문제(정렬하려는 리스트)가 더 단순한 하위 문제(부분 리스트)로 축소됨.

  2. 하위 문제가 충분히 작아지면 더 간단하고 빠르게 처리 가능.

2. 2. Conquer(정복)

“분할된 작은 문제들을 각각 해결하고, 결과를 합쳐서 전체 문제를 해결하는 과정”
-> 분할한 하위 리스트들을 각각 재귀적으로 정렬한 후, 합치는 과정이 핵심.

예시: 병합 정렬에선 작은 부분 리스트들이 정렬된 상태로 돌아오면, 두 리스트를 병합(merge)하는 작업을 수행.

예시: 퀵 정렬에선 피벗 기준으로 나눈 하위 리스트들을 각각 정복하는 작업을 수행(정렬)

Divide & Conquer 장점

1. 복잡한 문제를 효율적으로 해결 (Efficiently solve difficult problems)

핵심 아이디어: “큰 문제를 작게 쪼개면(분할), 각 부분 문제를 더 쉽게 해결할 수 있고, 그 결과를 합쳐서 원래 문제를 해결.”

예: 정렬 알고리즘(병합 정렬, 퀵 정렬) / 고급 문제(분할 정복으로 푸는 수학 문제 등)

실제 효과
큰 문제에 직접 달려드는 것보다, 더 단순한 작은 문제로 나누면 논리적·구현적 복잡도가 낮아짐.

재귀(Recursion)와 결합해, 문제를 단계적으로 해결 가능.

2. 병렬 처리(Parallelism)에 유리

분할한 하위 문제들이 서로 독립적인 경우가 많아, 병렬로 실행할 수 있음.

예: 병합 정렬을 병렬화할 때, 왼쪽 부분 리스트와 오른쪽 부분 리스트를 멀티프로세서에서 동시 처리한 뒤 결과를 병합.

실제 효과
멀티코어/멀티프로세서 환경에서 처리 속도 향상.

공유 메모리를 활용해 각 코어가 별도의 하위 문제를 처리하고, 최종 결과만 합침.

3. 메모리 접근(Memory access)의 효율성

하위 문제들이 작은 크기의 데이터를 다루므로,

캐시(cache) 활용도가 높아져서 메인 메모리 직접 접근 시간을 줄일 수 있음.

실제 효과
작은 배열을 정렬할 때 캐시에 전부 적재해 작업하면, 메모리 병목이 덜함.

Divide and Conquer는 작은 문제 여러 개를 순차/병렬로 풀기 때문에, 캐시 적중률(Cache hit rate)이 올라갈 수 있음.

4. 기타 장점 (And more)

코드 구조가 직관적: 재귀적 설계로 명확한 로직을 구현 가능.

다양한 문제(정렬, 선택, 행렬 연산, FFT 등)에 유연하게 적용 가능.

알고리즘의 재사용성 높음: 분할 정복 템플릿을 여러 문제에 응용.

Merge Sort (병합 정렬)

1. 직관(Intuition)

1️⃣ 분할(Divide)

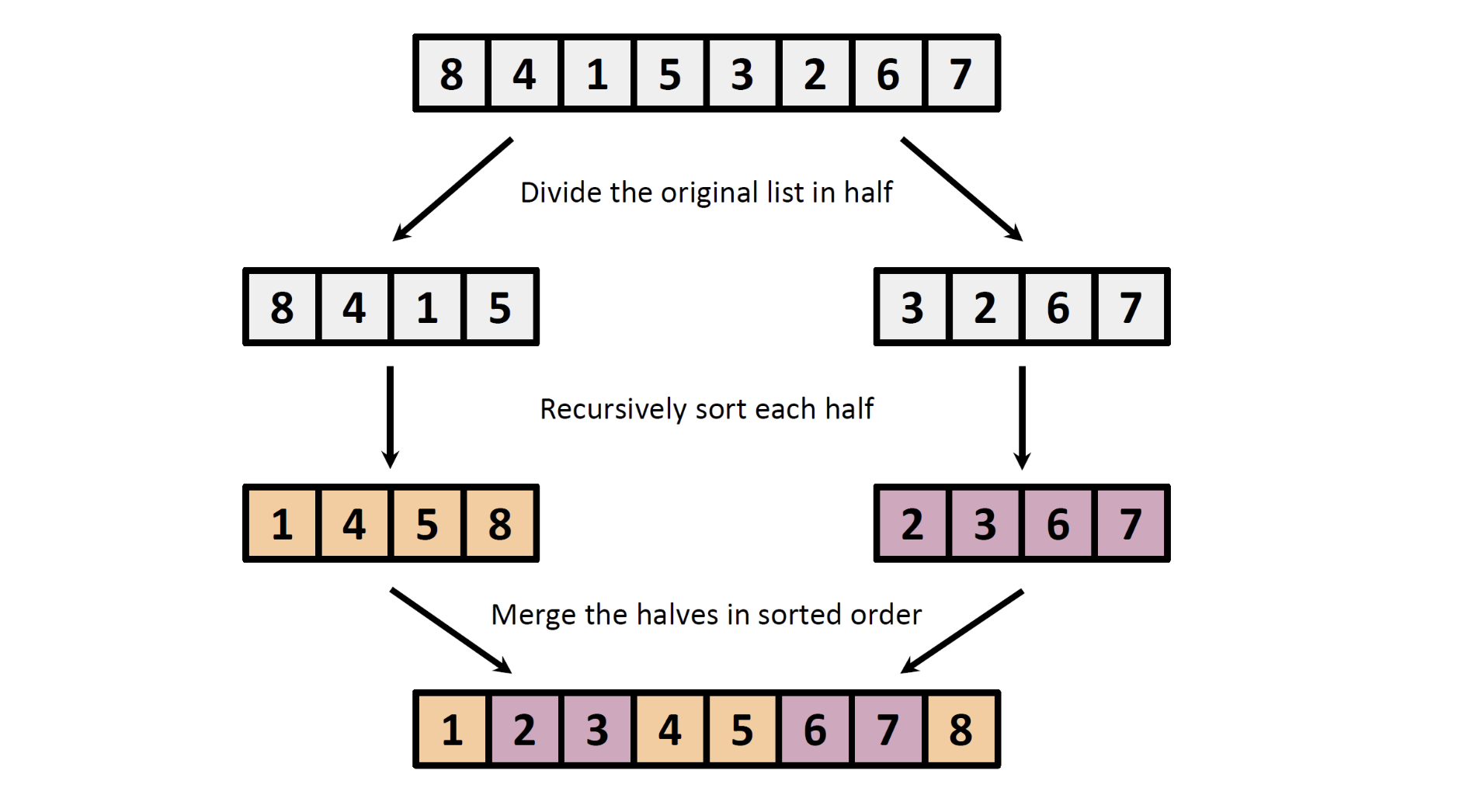
  • 리스트(배열)를 정확히 절반으로 나눈다.
  • 예:8,4,1,5,3,2,6,7 → 왼쪽 8,4,1,5, 오른쪽 3,2,6,7

2️⃣ 정복(Conquer / 재귀적 정렬)

  • 나눈 리스트 각각을 재귀적으로 정렬한다.
  • 나중에는 길이가 1개~2개 정도가 되면, 더 이상 나눌 수 없을 때 간단히 정렬 가능.

3️⃣ 합치기(Merge)

  • 이미 정렬된 두 리스트를 하나의 정렬된 리스트로 병합(Merge)한다.
  • 이 단계에서 정렬이 이루어지는 핵심 과정이 일어난다.

2. Merge Sort 의사코드

MERGE-SORT(A, p, r)
    if p < r// p와 r이 같으면(즉, 부분 배열의 크기가 1), 더 이상 나눌 수 없으므로 정렬이 끝난 상태
        q = floor((p + r) / 2)	// 중간 인덱스를 구함
        MERGE-SORT(A, p, q)	// 왼쪽 부분 배열 A[p..q]을 재귀적으로 정렬
        MERGE-SORT(A, q + 1, r) // 오른쪽 부분 배열 A[q+1..r]을 재귀적으로 정렬
        MERGE(A, p, q, r) // “이미 정렬된” 왼쪽 구간 A[p..q]과 오른쪽 구간 A[q+1..r]을 하나의 정렬된 배열로 병합

A: 정렬할 배열(리스트)

p: 배열의 시작 인덱스 (예: 0)

r: 배열의 끝 인덱스 (예: A.length - 1)

q: 중간 지점 (p와 r의 중간)

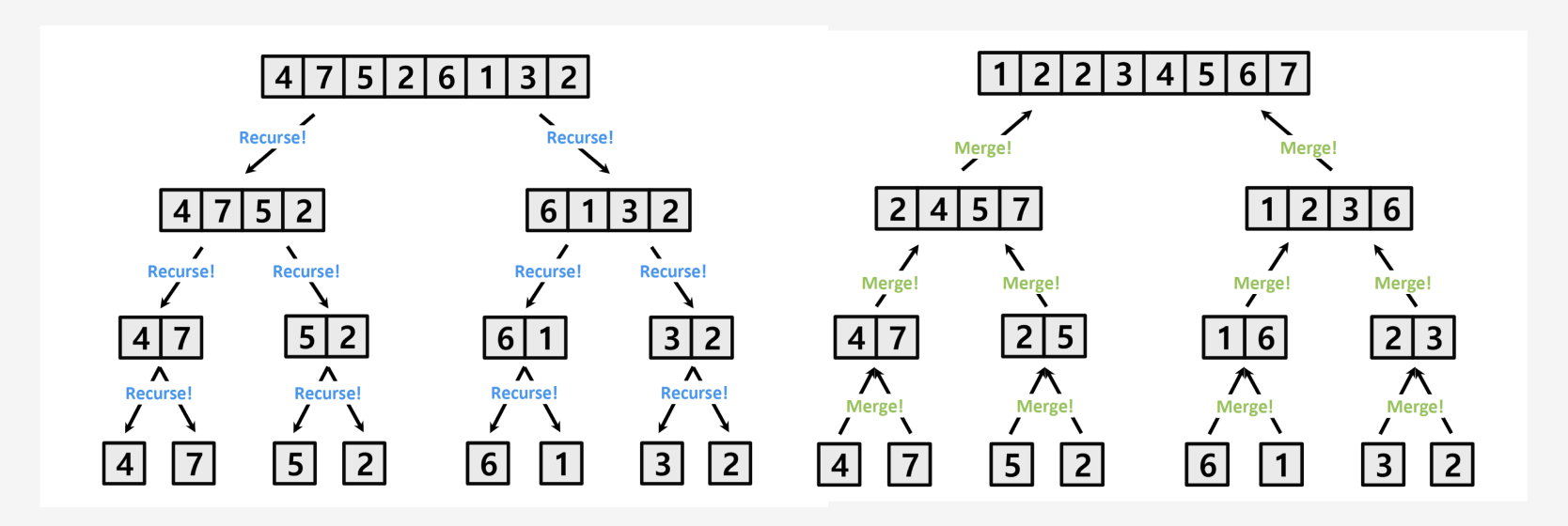
3. 실제 병합 단계 의사코드

MERGE(A, p, q, r)
    n1 = q - p + 1
    n2 = r - q

    # 새 배열 L, R 생성 (크기는 각 부분 리스트 길이 + 1)
    let L[1..n1 + 1] and R[1..n2 + 1] be new arrays

    for i = 1 to n1
        L[i] = A[p + i - 1]

    for j = 1 to n2
        R[j] = A[q + j]

    L[n1 + 1] = ∞
    R[n2 + 1] = ∞

    i = 1
    j = 1

    # 병합(merge) 과정
    for k = p to r
        if L[i] ≤ R[j]
            A[k] = L[i]
            i = i + 1
        else
            A[k] = R[j]
            j = j + 1

(1) n1, n2 계산

n1 = q - p + 1는 왼쪽 부분 리스트의 길이
n2 = r - q는 오른쪽 부분 리스트의 길이

(2) L, R 배열 생성

크기가 n1+1과 n2+1인 임시 배열 L, R을 만듦.
각각 왼쪽 부분 배열(A[p..q])과 오른쪽 부분 배열(A[q+1..r])의 내용을 복사함.

(3) sentinels (L[n1+1], R[n2+1])

∞(무한대) 값을 넣어 경계 처리를 함.
이렇게 하면 인덱스를 벗어나지 않도록 안전 장치가 됨.
즉, 어느 한쪽 배열의 모든 원소를 이미 다 썼을 때도, 비교 절차에서 에러 없이 계속 진행 가능.

(4) i, j 초기화

i, j는 각각 L과 R을 가리키는 인덱스(1부터 시작)

(5) 메인 병합 루프 (for k = p to r)

실제로 A[p..r] 구간에 정렬된 데이터를 채워 넣는 작업

L[i]와 R[j]를 비교해 더 작은 쪽을 A[k]에 넣는다.

그 다음 해당 배열의 인덱스(i 또는 j)를 1 증가해서, 다음 원소를 비교 준비

한 바퀴 돌 때마다 A[k] 위치에 가장 작은 원소를 확정해나감.

병합정렬에서의 Proving correctness

이제 병합정렬이 어떻게 되먹은 놈인지, 어떻게 굴러가는지 알게되었다.
그렇다면 이제 이 알고리즘이 잘 돌아가는지 확인해봐야할 차례이다.
정확성 증명에서 가장 중요한 것은 무엇이라고 했을까?
바로 Loop Invariant (반복문 불변식)이다.

지금 당장 이 Loop Invariant와, 정확성 증명의 3단계가 무엇인지 속으로 읊어보자.
만약 좔좔 흘러나오지 않는다면, 이 시리즈의 1번으로 돌아가서 복습하고 오길바란다.

병합 정렬에서의 Loop Invariant

✔️ (1) 첫 번째 불변식

  • 반복문의 매 반복 시작 시점에서, A[p..k-1] 부분 배열은
    L[1..n1+1]과 R[1..n2+1] 중 가장 작은 k-p개의 원소를 정렬된 상태로 포함한다.

미친~ 뭔 소린지 하나~도 모르겠다.
원래 증명식이란게 저런식으로 풀어두면 되게 이해하기가 어렵다.

일단 "가장 작은 k-p개의 원소" 👈 이것부터가 문제다.
가장 작은 (k−p)개라는 말은,
현재 A[p]부터 A[k-1]까지 총 k - p개의 칸이 채워졌다는 뜻이고,
그 칸들엔 L과 R에서 가장 작은 원소들부터 차례대로 정렬된 상태로 들어가 있다는 말이다.

...당연한 말 아닌가?
병합 정렬의 너무나도 기본적인 원리라는 것을 우리는 알고있다.
이렇게 쉬운 말을 함축적으로 적다보니 이런 사단이 난것이다.

그래도 무슨 말인지 와닿지 않는다면 예시를 들어보자!

L = [2, 4, 5, 7, ∞]
R = [1, 2, 3, 6, ∞]

A는 [ ..., ?, ?, ?, ?, ?, ?, ?, ?, ... ] 이고
p = 9, k = 13이라고 해보면
k - p = 4니까 A[9] ~ A[12]까지 4개의 칸이 채워졌고

그 안에는 L과 R에서 가장 작은 4개가 정렬된 상태로 들어가 있다는 거다.
즉, A[9..12] = [1, 2, 2, 3] ← L과 R에서 작은 순서대로 가져온 것!

📦 비유: L과 R은 박스, A는 진열대

그래도 이해가 가지않는 당신은 지금부터 마트 직원이다.
그리고 두 개의 상자(= L, R)에 각각 작게 정렬된 상품들이 들어 있다.
당신은 이 상자들에서 하나씩 꺼내서, 진열대 A 위에 왼쪽부터 차례대로 정리하고 있다.

꺼낼 때는 항상 각 상자에서 맨 앞에 있는 가장 작은 상품을 꺼낸다
그래서 진열대에 지금까지 진열한 상품들은 항상 정렬된 상태로 놓이게 된다.

🔁 루프가 돌고 있다는 건?

진열대에서 A[p]부터 A[k-1]까지는 지금까지 정리한 부분이다.
여기에 있는 것들은 상자 L, R에서 가장 작은 것들부터 차례대로 꺼낸 것이기 때문에 당연히 정렬돼 있다.

✅ 이게 바로 첫 번째 루프 불변식

"A[p..k−1]에는 L과 R에서 아직 꺼내지 않은 것들 중
가장 작은 (k−p)개가 들어 있고, 그것들은 항상 정렬된 순서로 있다."를 풀어 설명한 것

🧠 한마디로 말하면?

지금까지 진열한 부분(A[p..k-1])은 항상 정렬돼 있다.
왜? 늘 상자(L, R)에서 가장 작은 것부터 꺼내니까!

✔️ (2) 두 번째 불변식

L[i]와 R[j]는 아직 A로 복사되지 않은 L과 R의 원소들 중 가장 작은 값이다.

업로드중..

L[i], R[j] 둘 중 작은 값을 계속 A에 채워 넣는 방식이기 때문에,
이 값들이 현재 남은 후보들 중 최솟값을 대표한다는 성질이 항상 유지된다.
두 번재 불변식은 이해가 쉽게 갈 것이다.
그래도 이해가 안간다면,,,위에서부터 다시한번 읽고오도록

profile
이동윤
이전 포스트

Ch3. Algorithmic Analysis III

다음 포스트

Ch4-2. Divide and Conquer II

0개의 댓글