이진 트리
검색을 위한 자료구조 → 하나의 부모가 두 개의 자식만 가짐
균형이 맞지 않으면 선형검색(O(1)) 급으로 떨어지지만 잠재력이 가장 큼
균형이 맞다면 O(logN)의 성능을 보임
이를 보완하고자 나온 것 → B-tree
B-Tree
인덱스를 이루고 있는 자료구조의 일종
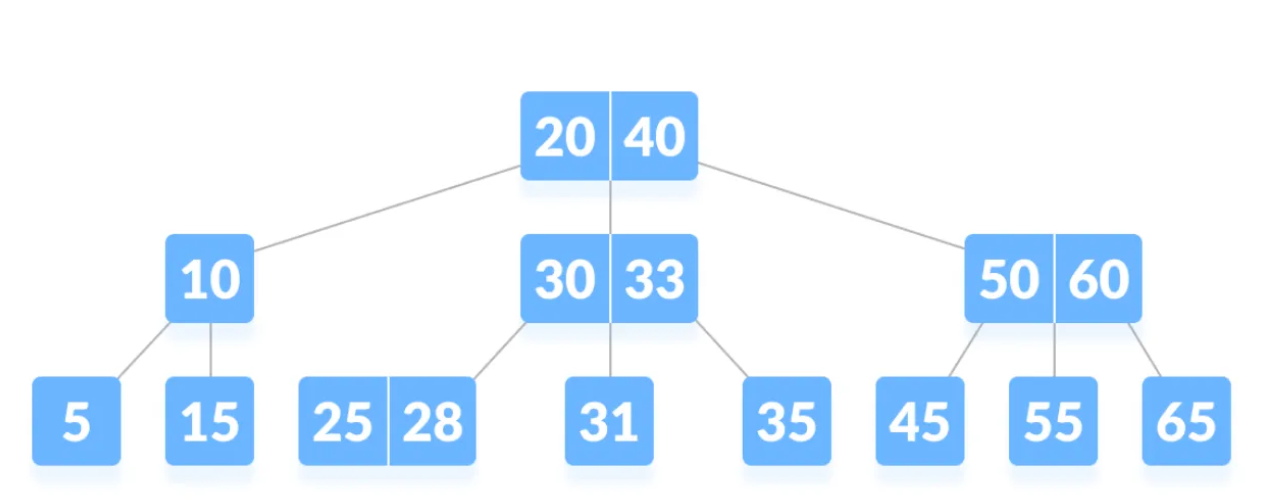
더 많은 자식을 가질 수 있음
B+Tree
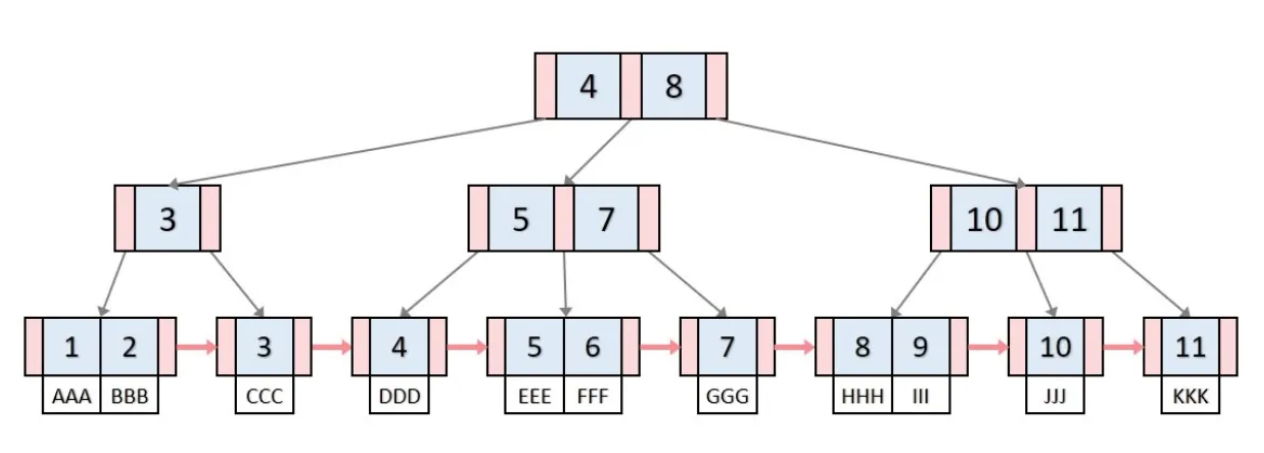
리프 노드들이 서로 연결돼있어서 B-Tree에 비해 순차 접근이 매우 효율적이다.
리프 노드만 실제 데이터를 저장하고 있다. 내부 노드는 인덱싱 역할
2-3 Tree
균형 이진 트리의 일종으로, 각 노드는 2개나 3개의 자식을 가질 수 있음
2-3-4 Tree
2-3 Tree를 확장한 버전으로, 각 노드가 2, 3, 또는 4개의 자식을 가질 수 있음
AVL Tree
이진 탐색 트리의 일종으로, 각 노드에서 왼쪽 및 오른쪽 서브트리의 높이 차가 1 이하로 유지되는 트리임
Red Black Tree
얘도 결국 이진 트리임
인덱스 → 한번의 I/O로 최대의 값을 가져오게 하기 위해, I/O 수를 줄이기 위해
그렇다면, B+Tree가 B-Tree에 비해 반드시 좋다고 할 수 있을까요? 그렇지 않다면 어떤 단점이 있을까요?
단순 하나의 값을 찾을 때는, B-Tree가 좋을수도 있음
B+Tree는 무조건 리프노트까지 내려가야 값을 얻을 수 있음
하지만 범위연산을 해야되기 때문에 이것은 의미가 없을수도있다.
DB에서 RBT를 사용하지 않고, B-Tree/B+Tree를 사용하는 이유가 있을까요?
RBT(레드블랙트리)는 메모리 내 작업에서 성능이 뛰어나기는 하지만, 디스크 기반 데이터베이스의 요구사항에는 부적합함. 결국 얘도 2-3트리이기 때문이다.
B Tree는 Depth가 줄어들기 때문에, 최대한 적게 검색한다.
오름차순으로 정렬된 인덱스가 있다고 할 때, 내림차순 정렬을 시도할 경우 성능이 어떻게 될까요? B-Tree/B+Tree의 구조를 기반으로 설명해 주세요.
오름차순으로 정렬돼있다는건 반대로 보면 내림차순이다.
그렇기 때문에 성능은 같지 않을까?
인덱스
추가적인 쓰기 작업과 저장 공간을 활용하여 데이터베이스 테이블의 검색 속도를 향상시키기 위한 자료구조
- Main Index
기본적으로 인덱스가 Default로 생긴다 → 보통은 PK인데, 바꿀수도 있는듯 [이게 근데 클러스터드 인덱스임]
- 클러스터드 인덱스는 반드시 하나만 존재한다.
- 테이블 전체가 정렬된 인덱스가 되는 방식의 인덱스 종류이다. 실제 데이터와 무리(cluster)를 지어 인덱싱 되므로 클러스터형 인덱스라고 부른다. 데이터와 함께 전체 테이블이 물리적으로 정렬된다.
- 만약 PK가 없으면, Unique 컬럼이 대체.
- Unique마저 없으면, 내부적으로 숨겨져있음.
- Secondary Index
만약 더 필요하면 Secondary Index를 만든다. → 얘는 따라가면 결국 클러스터드 인덱스의 키값임
인덱스가 많으면 생성, 수정, 삭제일때는 성능이 떨어진다. → 인덱스 추가작업을 해야되기 때문에
반대로 조회 성능은 향상된다.
비클러스터드 인덱스는 왜 키값(PK)을 참조할까?
- 데이터가 추가, 수정, 삭제되면 클러스터드 인덱스의 메모리 구조가 바뀜
- 비클러스터드 인덱스에 키값을 박아두면, 위의 구조가 바껴도 상관이 없음
- 직접 값을 참조하게 되면, 세컨더리 인덱스까지 바꿔야함
느낀점
첫 cs 스터디에서 했던 내용들이다. 한 주제에 대해 두 시간씩 토론하는 방식인데 연결연결하면서 이건 뭐고 이건 뭐고... 이런식? 이거 하면서 cs 너무 재미있다고 생각하게 된 주제라 벨로그에 꼭 올리고 싶었다.
물론 제대로 정리된 건 아닌 것 같지만 날것의 내 모습을 올리고 이후에 발전한 모습을 보여주자... 느낌 은 아니고 그냥 추억을 기록하기 위함임.
참고자료
[자료구조] b tree & b+ tree
[MySQL] B-tree, B+tree란?
데이터베이스 인덱스 (2) - 클러스터형 인덱스와 비클러스터형 인덱스
자료구조-그림으로-알아보는-B-Plus-Tree
