ARIMA모델은 AR(Autoregression)모형과 MA(Moving Average)모형을 합친 모형으로, 시계열 데이터의 정상성을 가정한다.
정상성: 평균,분산이 시간에 따라 일정한 성질
비정상성인 데이터는 정상성을 갖도록 로그변환, 차분한다.
1) 변동폭이 일정하지 않은 경우 > 로그 변환
2) 추세, 계절성이 존재하는 경우 > 차분
AR모형: 자기회귀모형으로, 이전 관측값의 오차항이 이후 관측값에 영향
MR모형: 이동평균모형으로, 관측값이 이전의 연속적인 오차항의 영향을 받음
ARIMA(p,d,q)모형: d차 차분한 데이터에 AR(p)모형과 MA(q)모형을 합친 모형
따라서 AR(p)=ARIMA(p,0,0), MA(q)=ARIMA(0,0,q)이다.
p와 q는 ACF그래프와 PACF 그래프를 그려서 확인한다.
(p+q<2 or pxq=0을 포함한 짝수인 경우 좋은 파라미터)
-AR: PACF
-MA: ACF
ACF
: 시차에 따른 관측치들 사이의 관련성을 측정하는 함수
정상성을 가진 데이터는 상대적으로 빠르게 0으로 수렴하고, 비정상 시계열은 천천히 감소한다. 따라서 ACF는 정상성을 판단하는데 유용하다.
PACF
: 시차가 다른 두 시계열 데이터 간의 관련성을 측정하는 함수
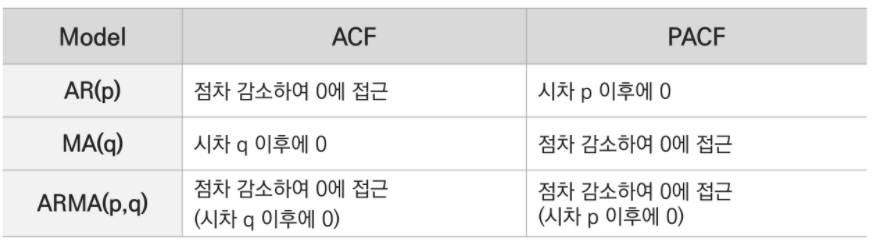
출처: https://leedakyeong.tistory.com
ACF, PACF
from statsmodels.graphics.tsaplots import plot_acf,plot_pacf
p,axes= plt.subplots(1,2,figsize=(10,4))
plot_acf(df['Price'],ax=axes[0]) #q=0
plot_pacf(df['Price'],ax=axes[1]) #p=1
plt.show()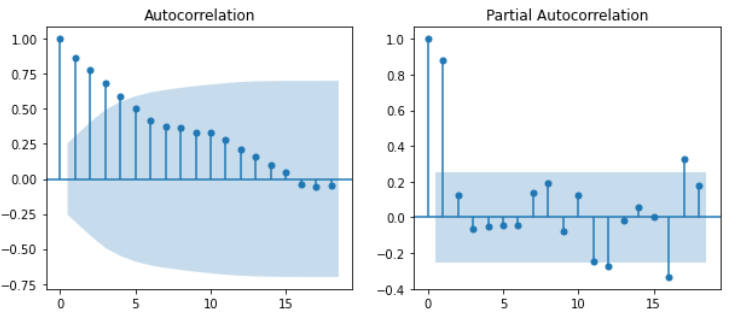
차분
df['Price2']=df['Price'].diff(1) #1차분
df.head()p,axes= plt.subplots(1,2,figsize=(10,4))
plot_acf(df['Price2'].iloc[1:],ax=axes[0])
plot_pacf(df['Price2'].iloc[1:],ax=axes[1])
plt.show()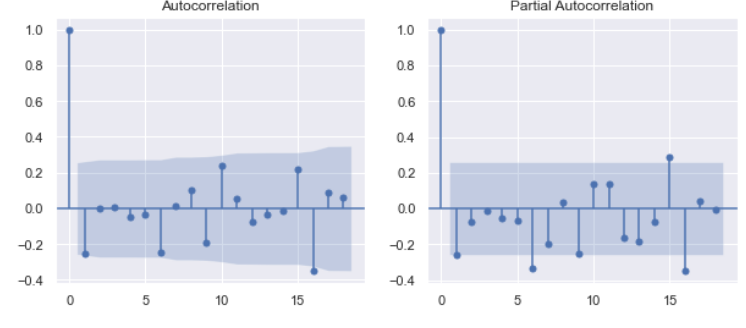
Summary
from statsmodels.tsa.arima_model import ARIMA
# (AR = 1, 차분 =1, MA=0) 파라미터로 ARIMA 모델을 학습한다.
model=ARIMA(df['Price2'].iloc[1:],order=(1,1,0))
fit_res=model.fit()
print(fit_res.summary())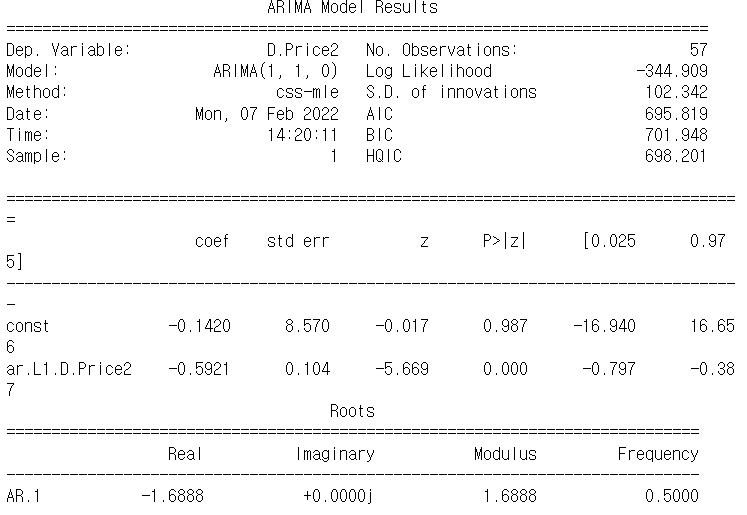
예측
#학습 데이터에 대한 예측 결과
fit_res.plot_predict()
#plt.figure(figsize = (10,4))
sns.set(rc={'figure.figsize':(6,4)})
plt.show()
