회귀분석
: 입력변수의 X의 정보를 활용하여 출력변수인 Y를 예측하는 방법
PART 01.
1. 단순 선형 회귀분석
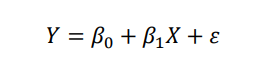
-입력 변수가 X, 출력 변수가 Y일 때, 단순선형회귀의 회귀식은 검은 선으로 나타낼 수 있음
-B0은 절편(intercept),B1은 기울기(slope)이며 합쳐서 회귀계수(coefficients)로 불림
-실제로 B0와 B1은 구할 수 없는 계수로 데이터(학습집합)을 통해 이 둘을 추정해서 사용 (e는 우리가 알지 못하는 값이라 0으로 추정)
2. 회귀계수 추정
-어떻게 추정할까?
실제값과 추정한 값의 차이를 잔차(residual)라고하며, 이를 최소화하는 방향으로 추정
최소 자승법
최소제곱법, 또는 최소자승법, 최소제곱근사법, 최소자승근사법(method of least squares, least squares approximation)은 어떤 계의 해방정식을 근사적으로 구하는 방법으로, 근사적으로 구하려는 해와 실제 해의 오차의 제곱의 합(SS)이 최소가 되는 해를 구하는 방법이다. (출처:위키백과)
3. 회귀계수의 의미
1) 회귀계수의 해석
-B1의 해석:X1이 1단위 증가할 때마다 Y가 B1만큼 증가한다
2) 선형 회귀의 정확도 평가 (회귀 모델에 대한 적합도 확인 방법: 잔차 분석, 결정 계수)
-선형회귀는 잔차의 제곱합(SSE)을 최소화하는 방법으로 회귀 계수를 추정
즉, SSE가 작으면 작을수록 좋은 모델.
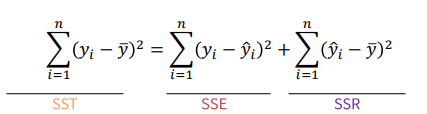
-MSE(잔차제곱의 평균)는 SSE(잔차제곱의 합)를 표준화한 개념
-SST = SSE + SSR
-Y의 총변동은 회귀직선으로 설명 불가능한 변동과 회귀직선으로 설명 가능한 변동으로 이루어져 있음
-R^2(결정계수)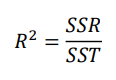
:RSE의 단점을 보완한 평가지표로 0~1의 범위를 가짐
R^2의 설명력으로 입력 변수인 X로 설명할 수 있는 Y의 변동을 의미하며,1에 가까울수록 선형회귀 모형의 설명력이 높다.
회귀 분석은 결국 Y의 변동성을 얼마나 독립변수가 잘 설명하느냐가 중요.
변수가 여러 개일 때 각각 Y를 설명하는 변동성이 크면 좋은 변수
-> p-value가 자연스레 낮아짐.
4. 회귀계수의 검정
-귀무가설: B1=0(회귀계수는 0이다, 즉 변수의 설명력이 없다.)
-대립가설: B1!=0(회귀계수는 0이 아니다, 즉 변수의 설명력이 존재)
PART 02.
1. 다중 선형 회귀분석
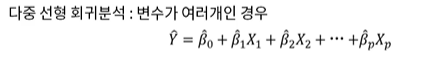
회귀계수 추정은 단순선형회귀분석과 동일하게 SSE를 최소화하는 방향으로 추정한다.
2. 다중 선형 회귀계수 검정
단순 선형 회귀계수 검정과 동일하다
3. 다중 선형 회귀모델 검정
귀무가설: B1=B2...BP=0 (모든 회귀계수는 0이다. 즉 변수의 설명력이 하나도 존재하지 않는다)
대립가설: 하나의 회귀계수라도 0이 아니다. (즉 설명력이 있는 변수가 존재한다)
-F검정을 통해 검정한다. (두 모집단의 분산의 차이가 있는가를 검정할 때 사용)
4. 다중공선성
다중공선성: 독립변수들 간에 강한 상관관계(선형관계)가 나타나는 문제이다. 이는 회귀분석의 전제 가정(독립변수들 간에 상관관계가 높으면 안된다)을 위배하는 것이므로 적절한 회귀분석을 위해 해결해야한다. 잘못된 변수 해석, 예측 정확도 하락 등을 야기시킨다.
진단방법
1.결정계수 R2값은 높아 회귀식의 설명력은 높지만 식 안의 독립변수의 P값(P-value)이 커서 개별 인자들이 유의하지 않는 경우가 있다.
2.독립변수들간의 상관계수(cor)를 구한다. (상관행렬 및 산점도 보고 판단!)
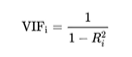
3. 분산팽창요인(Variance Inflation Factor,VIF)를 구하여 이 값이 10을 넘는다면 보통 다중공선성의 문제가 있다. (R^2>0.9인 경우,VIF >10)
해결방법
다중공선성을 근본적으로 해결하는 방법은 아직 없다.
1.상관관계가 높은 독립변수 중 하나 혹은 일부를 제거한다.(중요 변수만 선택)
2.변수를 변형시키거나 새로운 관측치를 이용한다.
3.자료를 수집하는 현장의 상황을 보아 상관관계의 이유를 파악하여 해결한다.
4.주성분 분석(PCA,Principle Component Analysis)를 이용한 diagonal matrix의 형태로 공선성을 없애준다.
PART 03.
1. 회귀분석-회귀모델의 성능지표
-AIC,BIC
2. 모델-모형의 성능지표
<회귀분석에서 사용하는 성능지표>
MSE(Mean Squared Error)

MSE는 실제 값과 예측 값의 차이를 제곱해 평균한 것.
MSE가 작을수록 좋지만, 과도하게 줄이면 과적합의 오류를 범할 가능성이 있다. 따라서 검증 집합의 MSE를 줄이는 방향으로 f를 추정 (주로 사용)
RMSE(Mean Squared Error)
MSE 값은 실제 오류 평균보다 더 커지는 특성이 있어 MSE에 루트를 씌운 RMSE 값을 쓴다.
MAE(Mean Squared Error)
실제 값과 예측 값의 차이를 절댓값으로 변환해 평균한 것
MAPE(Mean Absolute Percentage Error)
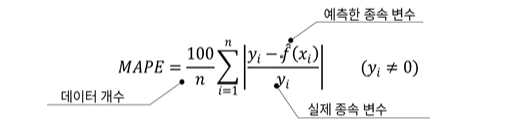
MAPE는 퍼센트 값을 가지며 0에 가까울수록 회귀 모형의 성능이 좋다고 해석할 수 있다. 0%~100% 사이의 값을 가져 이해하기 쉬우므로 성능 비교 해석이 가능
<분류에서 사용하는 성능지표 - Confusion Matrix>
-
정확도(Accuracy)
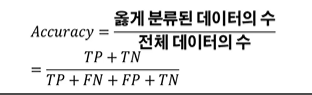
:전체 데이터 중에서 예측한 값이 실제 값과 부합하는 비율 -
정밀도, 재현율, 특이도
정밀도(precision): 예측이 참인 값 중 실제 참인 값
재현율(recall,Sensitivity,TPR): 실제 참인 값 중 예측도 참인 값
특이도(specificity): 예측이 거짓인 값 중 실제 거짓인 값
- G-mean, F1 measure

실제 데이터의 특성상 정확도보다는 제1종 오류와 제2종 오류 중 성능이 나쁜 쪽에 더 가중치를 주는 G-mean지표나 정밀도와 재현율만 고려하는 F1 measure가 더 고려해볼 수 있는 지표임. 둘 다 높으면 높을 수록 좋은 지표이다. (F1 measure가 더 자주 쓰인다.)
- ROC curve
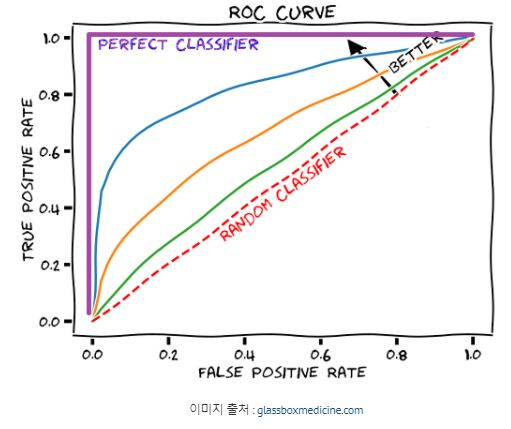
가로축을 1-특이도(FPR), 세로축을 재현율로 하여 시각화한 그래프.
이때 ROC curve의 면적을 AUC이며 0~1사이의 값을 가진다.
-AUC(area under the curve): ROC곡선 아래부분 면적
: AUC값은 클수록 좋다.
출처: 패스트캠퍼스 머신러닝&AI첫걸음 시작하기 2주차, 위키백과
