1. Clustering (군집분석)
각 데이터의 유사성을 측정하여 높은 대상 집단을 분류하고, 군집 간에 상이성을 규명하는 방법 (비지도학습이기 때문에 predict와 raw data와 대조하지 않는다.)
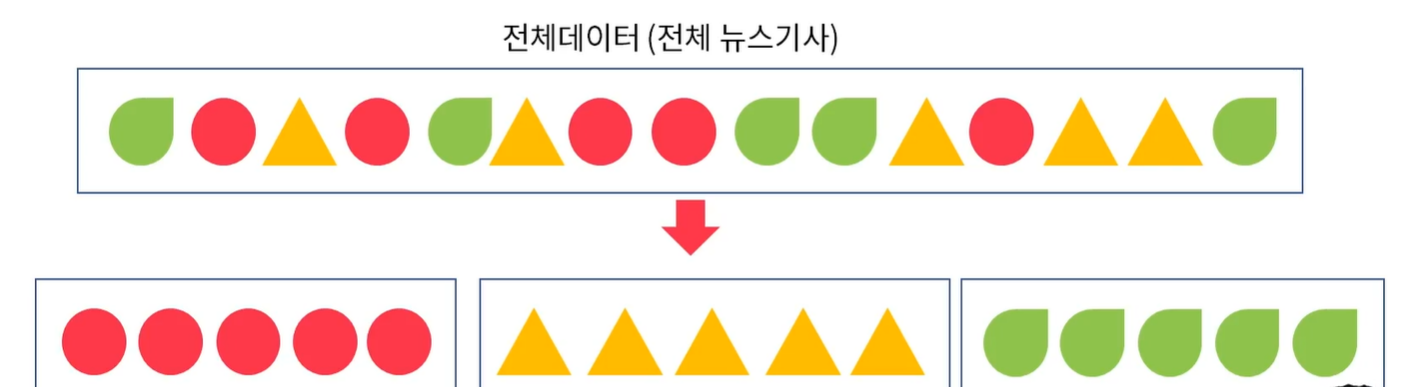
Clustering의 종류
-K-means Clustering: 데이터를 사용자가 지정한 K개의 군집으로 나눔
-Hierarchical Clustering(계층적 군집분석): 나무 모양의 계층 구조를 형성해나가는 방법
-DBSCAN: k개를 설정할 필요없이 군집화할 수 있는 방법
1) K-means Clustering
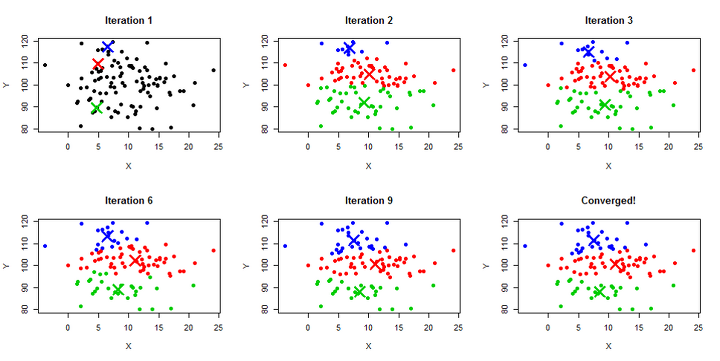
step 1. 각 데이터 포인트 i에 대해 가장 가까운 중심점을 찾고, 그 중심점에 해당하는 군집 할당
step 2. 할당된 군집을 기반으로 새로운 중심 계산, 중심점은 군집 내부 점들의 좌표의 평균(mean)으로 함
step 3. 각 클러스터의 할당이 바뀌지 않을 때까지 반복
from sklearn.cluster import KMeans
model = KMeans(n_cluster=3,random_state=42)
model.fit(df)
pred_label=model.predict(df)
print(pred_label[:5])
df['label']=pred_label.reshape(-1,1)
pd.crosstab(df['target'],df['label']) #군집화가 효과적으로 됐는지 확인#시각화
x,axes=plt.subplots(1,2,figsize=(10,3))
sns.scatterplot(df['sl'],df['sw'],hue=df['target'],ax=axes[0])
sns.scatterplot(df['sl'],df['sw'],hue=df['label'],ax=axes[1])
plt.show()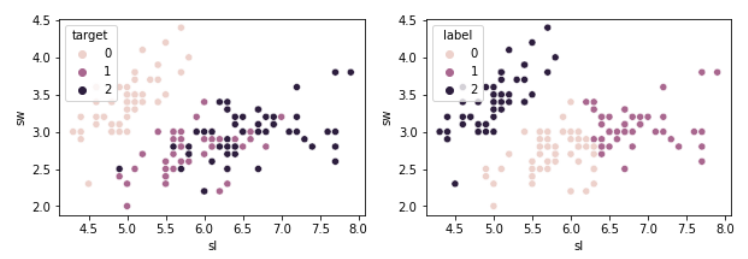
- 왜곡 정도가 매우 높은 데이터에 k-Means를 적용하면 중심의 개수를 증가시키더라도 변별력이 떨어지는 군집화가 수행된다.
따라서 로그변환/스케일링 후 군집분석한다.
from sklearn.preprocessing import StandardScaler
scaler=StandardScaler()
fit_scaler=scaler.fit_transform(df)
scaler_df = pd.DataFrame(data=fit_scaler,columns=['sl_s','sw_s'])
scaler_df['target'] = df['target']
scaler_df.head()
model = KMeans(n_clusters=3, random_state=42)
model.fit(scaler_df[['sl_s','sw_s']])
pred_label = model.predict(scaler_df[['sl_s','sw_s']])
print(pred_label[:5])
scaler_df['label'] = pred_label.reshape(-1,1)
pd.crosstab(scaler_df['target'], scaler_df['label']) #확인용점과 점 사이의 거리 측정
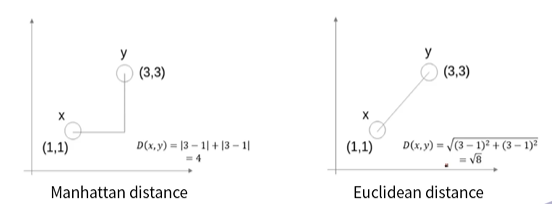
유클리디안 거리: 점과 점 사이의 가장 짧은 거리를 계산하는 거리 측정 방식
맨하탄 거리: 각 축에 대해 수직으로만 이동하여 계산하는 거리 측정방식
K값을 설정하는 방법
-군집의 개수 K는 사용자가 임의로 정하는 것이기 때문에, 데이터에 최적화된 K를 찾기 어려움
-K를 설정하는 대표적인 방법은 Elbow method,Silhouette method 등이 있음
1) Elbow method
n_clusters_list = [2,3,4,5,6]
inertia_list=[]
for k in n_clusters_list:
model=KMeans(n_clusters=k,random_state=42)
model.fit(df)
inertia_list.append(model.inertia_)
print(inertia_list)plt.plot([2,3,4,5,6],inertia_list)
plt.xlabel("K cluster count")
plt.ylabel("Sum of squared distances")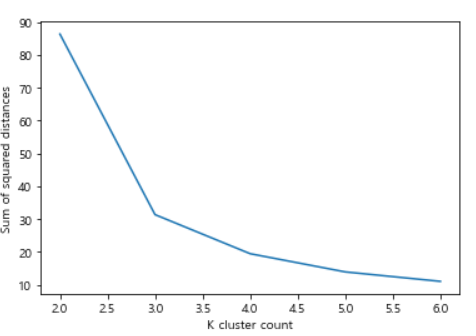
2) Silhouette method
from sklearn.metrics import silhouette_samples, silhouette_score
#실루엣 계수 silhouette_samples
scoef=silhouette_samples(df,labels=df['label'],metric='euclidean')
print(scoef[:5])
df['scoef']=scoef.reshape(-1,1) #실루엣 계수 변수 추가#전체 실루엣 계수 평균=np.mean(silhouette_samples())
sil_score=silhouette_score(df,labels=df['label'],metric='euclidean',random_state=42)
print(sil_score)
df.groupby('label')['scoef'].mean().sort_values(ascending=False)실루엣 계수는 -1에서 1 사이의 값을 가지며, 1로 가까워질수록 근처 군집과 더 멀리 떨어져 있는 것이고 0에 가까워질수록 근처 군집과 가까운 것이다.
K-means Clustering의 단점
-초기 중심 값에 민감한 반응을 보임
-noise와 outlier에 민감함
-군집의 개수 k를 설정하는 것이 어려움
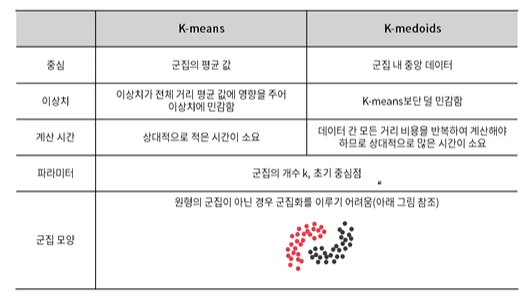
K-medoids Clustering
K-means Clustering의 변형으로, 군집의 무게 중심을 구하기 위해 데이터의 평균 대신 중간점(medoids)을 사용한다. 아래 그림의 결과를 보면 K-medoids의 중앙점이 더 명확하다. (이는 더 좋은 군집을 형성하게 될 가능성을 높임)
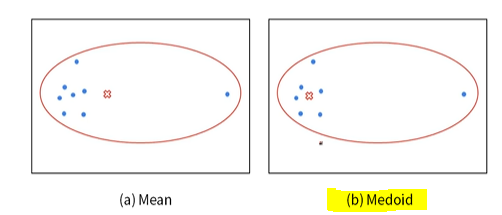
K-means VS K-medoids
2) Hierarchical Clustering
: 개체들을 가까운 집단부터 순차적/계층적으로 차근차근 묶어나가는 방식.
유사한 개체들이 결합되는 dendogram을 통해 시각화 가능.
사전에 군집의 개수를 정하지 않아도 수행 가능.
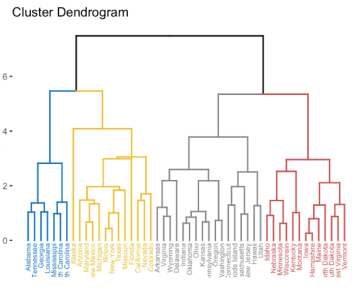
-모든 개체들 사이의 거리에 대한 유사도 행렬 계산
-거리가 인접한 관측치끼리 cluster 형성
-유사도 행렬 update
<참고>
1) https://scikit-learn.org/stable/auto_examples/cluster/plot_agglomerative_dendrogram.html
2)https://docs.scipy.org/doc/scipy/reference/generated/scipy.cluster.hierarchy.linkage.html
#방법1) sklearn.cluster. Agglomerative Clustering
from scipy.cluster.hierarchy import dendrogram
from sklearn.cluster import AgglomerativeClustering
def my_dendrogram(model, **kwargs):
counts = np.zeros(model.children_.shape[0])
n_samples = len(model.labels_)
for i, merge in enumerate(model.children_):
current_count = 0
for child_idx in merge:
if child_idx < n_samples:
current_count += 1 # leaf node
else:
current_count += counts[child_idx - n_samples]
counts[i] = current_count
linkage_matrix = np.column_stack(
[model.children_, model.distances_, counts]
).astype(float)
# Plot the corresponding dendrogram
dendrogram(linkage_matrix, **kwargs)
# setting distance_threshold=0 ensures we compute the full tree.
model = AgglomerativeClustering(distance_threshold=0, n_clusters=None)
model = model.fit(df[['pl','pw','sl','sw']])
plt.title("Hierarchical Clustering Dendrogram")
# plot the top three levels of the dendrogram
my_dendrogram(model, truncate_mode="level", p=3)
plt.xlabel("Number of points in node (or index of point if no parenthesis).")
plt.show()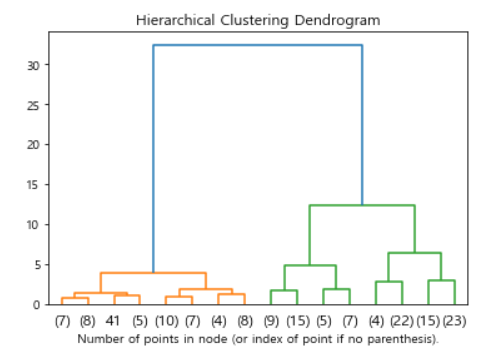
#방법2) scipy.cluster.hierarchy.linkage
from scipy.cluster.hierarchy import linkage
from scipy.cluster.hierarchy import dendrogram
arr =linkage(df[['pl','pw','sl','sw']],method='single',metric='euclidean')
#plt.xticks(rotation=45)
plt.figure(figsize=(30,5))
dendrogram(arr)
plt.show()Clustering간의 거리
-min,max,avg,centroids
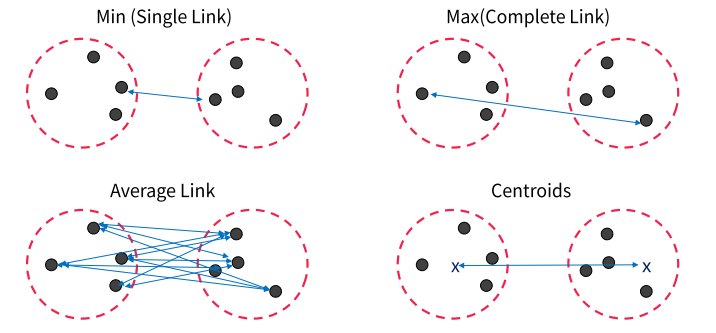
-Ward's method: 두 개의 클러스터가 병합되었을 때 증가되는 변동성의 양
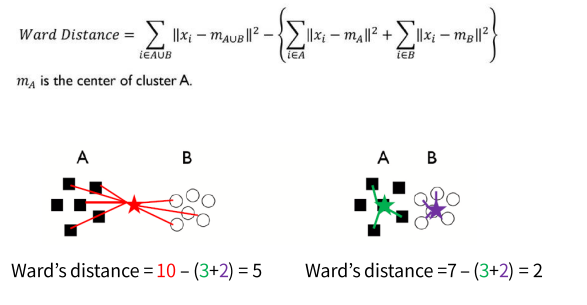
3) DBSCAN
:density-based clustering 중 가장 유명하고 성능이 우수하다고 알려져 있음.
DBSCAN의 특징은 eps-neighbors와 MinPts를 사용하여 군집을 구성.
eps-neighbors: 한 데이터를 중심으로 epsilon() 거리 이내의 데이터들을 한 군집으로 구성
MinPts: 한 군집은 MinPts보다 많거나 같은 수의 데이터로 구성됨.
만약 MinPts보다 적은 수의 데이터가 eps-neighbors를 형성하면 노이즈(noise)로 취급함.
DBSCAN 알고리즘 순서
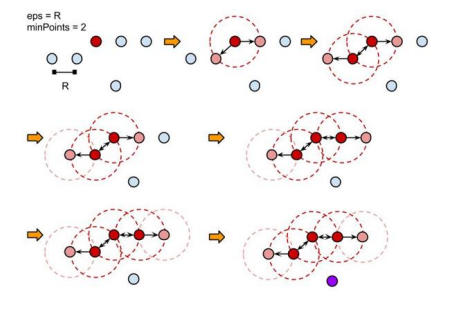
여기서 eps는 반지름의 크기이며, 이를 토대로 군집형성을 진행했다.
minpoints는 적어도 한 군집에 2개의 sample들이 모여야 군집으로 인정한다는 것이다.
DBSCAN 예시
최소거리 e 이내의 데이터들이 점진적으로 한 군집으로 합쳐지며 다양한 모양의 군집으로 형성한다.
(군집이 안된 데이터는 노이즈로 취급) -> outlier를 detection하는 분야에도 사용 가능

DBSCAN의 파라미터: MinPts,eps
:DBSCAN은 군집 분석을 적용하고자 하는 데이터에 대한 이해도가 충분할 때 파라미터 설정이 쉽다.

DBSCAN 장단점
장점
-k-means와 다르게 군집의 수를 설정할 필요가 없음
-다양한 모양의 군집이 형성될 수 있으며, 군집끼리 겹치는 경우가 없음
-노이즈 개념 덕분에 이상치에 대한 대응이 가능
-설정할 파라미터가 두 개(MinPts,eps)로 적으며, 적용 분야에 대한 사전 지식이 있는 경우 비교적 쉽게 설정이 가능
단점
-한 데이터는 하나의 군집에 속하게 되므로, 시작점에 따라 다른 모양의 군집이 형성됨
-Eps의 크기에 의해 DBSCAN의 성능이 크게 좌우됨
-군집 별로 밀도가 다른 경우 DBSCAN을 이용하면 군집화가 제대로 이루어지지 않음
from sklearn.cluster import KMeans,DBSCAN
model=DBSCAN(eps=0.5,min_samples=5, metric='euclidean')
pred_label=model.fit_predict(df) #predict 따로 없다.
print(pred_label[:5])
df['dbscan_label'] = pred_label.reshape(-1,1)
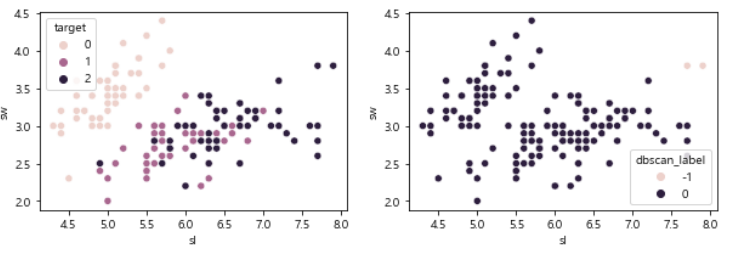
pd.crosstab(df['target'],df['dbscan_label']) #확인x,axes=plt.subplots(1,2,figsize=(10,3))
sns.scatterplot(df['sl'],df['sw'],hue=df['target'],ax=axes[0])
sns.scatterplot(df['sl'],df['sw'],hue=df['dbscan_label'],ax=axes[1])
plt.show()