[python]_numpy_3

Numpy 배열 연산

3. 집계 함수
   • Numpy 배열에 대해 집계 함수를 적용할 때는 반드시 axis로 설정된 기준에 따라 연산 수행
   • 별도로 값을 지정하지 않으면 기본값은 axis = None으로 지정
   • axis
     

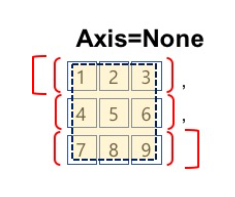
• axis = None
  전체 데이터를 하나의 배열로 간주하고 집계 함수의 연산 범위를 전체 배열로 지정

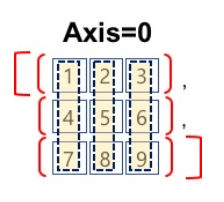
• axis = 0
  열을 기준으로 동일한 열에 있는 요소를 하나의 그룹으로 묶어 집계 함수의 연산 범위로 지정
  

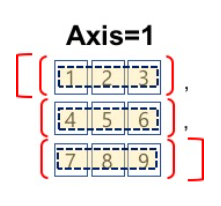
• axis = 1
  행을 기준으로 동일한 행에 있는 요소를 하나의 그룹으로 묶어 집계 함수의 연산 범위로 지정
  

• 집계 함수 : 배열객체에 대한 메소드로 사용하거나 Numpy 라이브러리의 메소드로 사용하는 두 가지 방법
  - 합계 : sum()
  - 최소값 : min()
  - 최대값 : max()
  - 누적 합계 : cumsum()
  - 평균 : mean()
  - 중앙값 : median()
  - 크기 순으로 나열된 데이터에 대해 중앙에 위치하는 값
  - 상관계수 : corrcoef()
  - 데이터 간의 상관관계를 나타내는 수치(-1 <= r <= 1)
  - 표준편차 : std()
  - 분산의 제곱근, 데이터가 평균으로부터 흩어져 있는 정도
  - 분산 = 편차(요소-전체평균)제곱의 평균
  - 고유값 : unique()

  ---

 # 사용할 배열 객체 확인
np_print(a)

합계

# 합계 - 전체 기준 => 모든 요소에 대한 합
# 1) 배열 타입의 메서드 : arr.sum()
# 2) numpy 함수 : np.sum(arr)
a.sum()

# 합계 - row, 가로축별 합산
# 메서드, np함수의 파라미터값 : axis=1
# 결과값 : [0번 row의 합, 1번 row의 합, 2번 row의 합...]
print(c.sum(axis=1))
print(c)

# 합계 - column 세로축별 합산 결과
# 메서드, np함수의 파라미터값 : axis=0
# 결과값 : [0번째 column합, 1번째 column합, 2번째 column합...]
print(c.sum(axis=0))
print(c)

최소값

# 최소값 - 전체 기준
# 1) 배열 타입의 메서드 : arr.min()
# 2) numpy 함수 : np.min(arr)
c.min()
np.min(c)

# (참고) 파이썬 리스트에서 최소값 찾기
x = [1, 2, 3, 4]
min(x)

# 최소값 - 각 가로축(row)별 최소값 찾기
# 결과값 : [0번째row 최소값, 1번째row최소값...]
print(c.min(axis=1))
print(c)
print(np.min(c, axis=1))

# 최소값 - 각 세로축(column)별 최소값 찾기
# 결과값 : [0번째column 최소값, 1번째column최소값...]
print(c.min(axis=0))
print(np.min(c, axis=0))

최대값

# 최대값 - 전체기준
# 1) 배열 타입의 메서드 : arr.max()
# 2) numpy함수 : np.max(arr)
c.max()
np.max(c)

# 최대값 - 가로축 기준(row)
c.max(axis=1)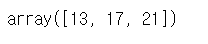

# 최대값 - 세로축 기준(column)
c.max(axis=0)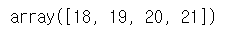

c

누적합계

# 누적합계 - 전체 기준
# 1) 배열 타입의 메서드 : c.cumsum()
# 2) numpy 함수 : up.cumsum()
# 결과값 : 
c.sum()  # 총합

c.cumsum() # 누적합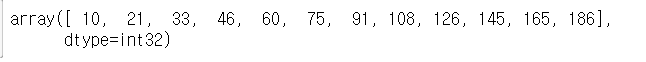

# 누적합계 - 가로축(row)기준
c.cumsum(axis=1)

# 누적합계 - 세로축(column)기준
c.cumsum(axis=0)

평균

# 평균 - 전체 기준
# 1) 배열 타입의 메서드 : arr.mean()
# 2) numpy 함수 : np.mean(arr)
print(c.mean())
print(np.mean(c))

# 평균 - 가로축 기준
print(c.mean(axis=1))
print(np.mean(c, axis=1))

# 평균 - 세로축 기준
print(c.mean(axis=0))
print(np.mean(c, axis=0))        

c

중앙값

# 중앙값 - 전체 기준
# numpy 함수 : np.median()
# arr.median()을 쓸 수 없음
# c.median()불가능
np.median(c)
> 요소의 개수가 짝수이면 중앙에 있는 두 값을 더해 2로 나눈 값을 구해준다.

# 중앙값 - 가로축 기준
np.median(c, axis=1)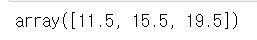

# 상관계수 : 두 데이터간의 상관관계(양/음의 상관관계)
# numpy 함수 : np.corrcoef(arr1, arr2)
x = np.array([15, 12, 27, 37, 29])
y = np.array([1, 4, 2, 9, 7])

상관계수

# 서로 다른 배열 2개를 활용한 상관계수 matrix
# 결과 : 대칭형 매트릭스(대각선을 경계로 상위, 하위 삼각형 중 하나만 해석해도 된다)
# 오른쪽 아래를 향하는 대각선은 자기 자신과의 상관관계(항상 1)
print(x)
print(y)
print(np.corrcoef(x, y))

# numpy에서는 3개요소를 이용한 상관도를 구하는 것이 불가능
# 팬더스를 이용하는 경우는 2개씩 짝지은 모든 경우의 수를 구해준다.
z = np.array([0.3, 0.5, 0.6, 0.8, 1.3])

np.corrcoef(x, y, z)

표준편차

# 표준편차 - 전체 기준
# 1) 배열 타입의 메서드 : arr.std()
# 2) numpy 함수 : np.std(arr)
a

# 전체
np.std(a)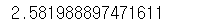

# 세로축
np.std(a, axis=0)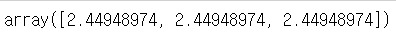

# 가로축
np.std(a, axis=1)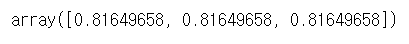

---

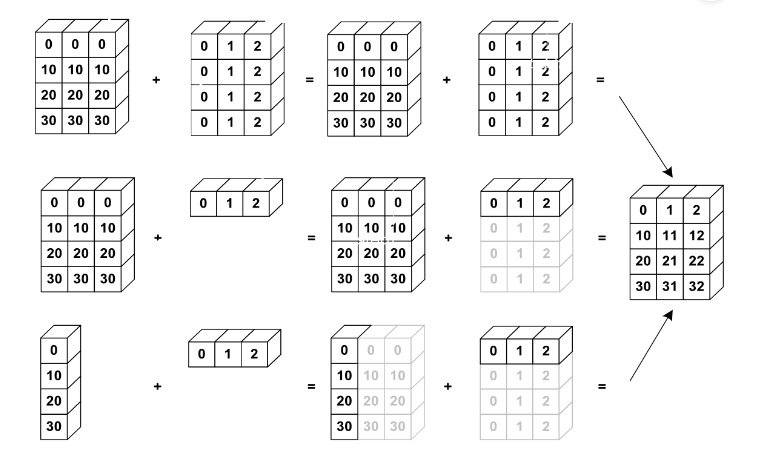
브로드캐스팅(BroadCasting)

• 서로 다른 구조(shape)를 가진 배열에 대해 연산을 수행할 때 구조를 맞추는 과정
• 배열과 스칼라값 간의 연산
• 배열과 배열 간의 연산
• 브로드캐스팅 규칙 : 축의 길이가 일치하거나 둘 중 하나의 길이가 1인 두 배열에 대해 호환성을 가짐

# 사용할 배열 객체 확인
np_print(a)
np_print(b)

1. 배열과 값(single value, scala)

• 스칼라 값을 배열의 구조와 동일한 배열로 변형하여 연산 수행

# 구조가 다른 배열간의 연산
# a배열의 모든 요소에 각각 10씩 더하기
a + 10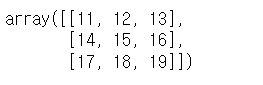

# 스칼라 -> 배열 변형
# 3행 3열의 구조에 모든 요소가 10인 배열 생성
scalar_arr = np.full_like(a, 10)
np_print(scalar_arr)

a + scalar_arr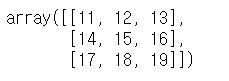

2. 서로 다른 구조의 배열

• 행, 열의 최대 길이를 기준으로 구조를 생성한 배열로 변형하여 연산 수행
• 확장된 행, 열에 대해서 기존 배열과 동일한 데이터로 구성

# 1행 4열의 구조에서 1, 2, 3, 4를 값으로 가지는 배열 x 생성
# 4행 1열의 구조에서 1, 2, 3, 4를 값으로 가지는 배열 y 생성
x = np.arange(1, 5).reshape(1, 4)
y = np.arange(1, 5).reshape(4, 1)

np_print(x)
np_print(y)

# 배열 X를 동일한 값으로 4행으로 확장한 새로운 배열 생성
# 행 방향으로 배열 추가(세로길이 증가) 메서드 : np.append(arr1, arr2, axis=0)
new_x = np.append(x, x, axis=0)
new_x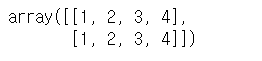

new_x = np.append(new_x, new_x, axis=0)
new_x

# 배열 y도 위의 수순대로 4열까지 확장한 새로운 배열로 저장해주세요.
# 열 방향으로 (column개수 증가) 배열 추가 메서드 np.append(), 방향 = 1

new_y = np.append(y,y,axis=1)
np_print(new_y)

new_y = np.append(new_y,new_y,axis=1)
np_print(new_y)

new_x + new_y

x + y