[Deep Learning] Optimization Method

📖 케라스 창시자에게 배우는 딥러닝 (프랑소와 숄레, 박해선, 길벗) 참고

🧸 Stochastic Gradient Descent

실제 신경망에서는 파라미터의 개수가 수천 개보다 적은 경우가 거의 없고, 수천만 개가 되는 경우도 종종 있기 때문에 이 전 포스트에서 언급한 gradient(f)(W) = 0을 풀어 가장 작은 손실 함수를 만드는 것은 어려운 일이다.

그래서 전체 데이터(batch) 대신 일부 데이터(mini-batch)만 사용하여 계산을 하는 방법이 바로 Stochastic Gradient Descent(SGD, 확률적 경사하강법)이다. 이는 전체 데이터를 사용하는 것보다는 부정확할 수 있지만 계산 속도가 훨씬 빠르다. 즉 같은 시간동안 더 많은 step을 이동할 수 있으며 일반적으로 batch 결과에 수렴한다.

Stochastic(확률적)이라는 단어는 각 배치 데이터가 무작위로 선택된다는 의미이다. (random의 과학적 표현이 stochastic)

• mini-batch stochastic gradient descent : 랜덤한 훈련 샘플 배치와 이에 상응하는 타깃으로 계산
• true stochastic gradient descent : 반복마다 하나의 샘플과 하나의 타깃을 뽑는 것
• batch stochastic gradient descent : 가용한 모든 데이터를 사용하여 반복 실행

🧸 Optimization Method

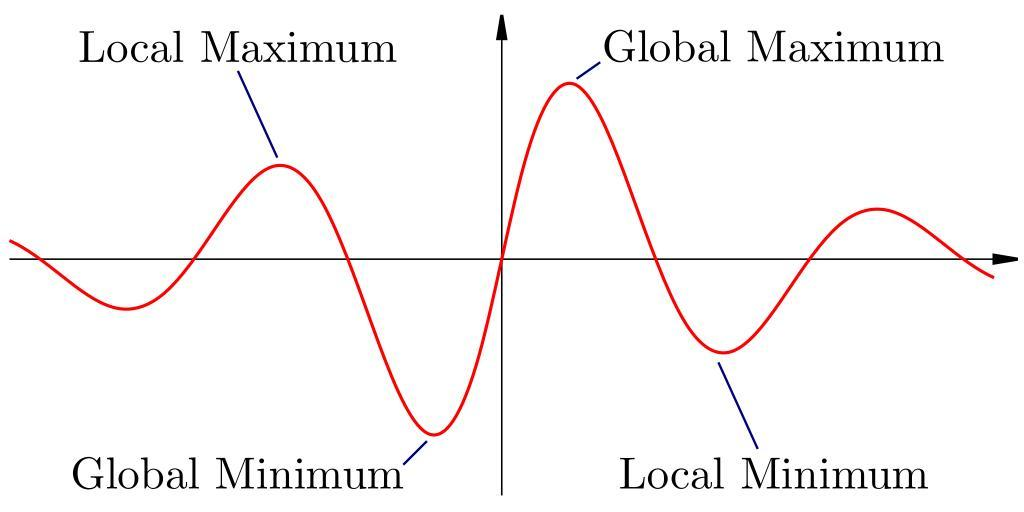
위 그림은 기울기가 0이 되는 지점이 2개 이상이다. 이를 nonconvex라고 표현하고 이와 반대로 최소점이 한 개, 즉 기울기가 0인 지점이 1개인 경우를 convex라고 표현한다. 우리는 전역 최솟값(Global Minimum)으로 도달하는 것이 목표지만 SGD로 최적화하게 되면 지역 최솟값(Local Minimum)에 갇히게 될 수 있다. 이를 해결하기 위해 SGD를 변경한 다양한 최적화 방법, Optimizatio Method들이 존재한다.

Momentum

모멘텀은 간단하게 표현해서 이동 과정에 관성을 반영하는 것이다. 과거에 이동했던 방향을 기억하여 이동에 반영하는 것이다. 즉 바로 직전 시점의 가중치 업데이트 변화량을 적용한다.

Adaptive Gradient(Adagrad)

학습 횟수가 증가하면 점점 최솟값에 가까워지는 것이기 때문에 학습률을 작게 조절하여 안정적으로 최솟값에 도달할 수 있도록 하는 방법이다. 학습률 감쇠식을 통해 학습률을 조정한다.

𝛾 = 𝛾 / (1+ 𝜌∙𝑛)
𝑔 = 𝑔 + (𝑑𝐸)^2
𝑊(𝑡+1) = (𝑊𝑡 − 𝛾) / (√𝑔 ∙ 𝑑𝐸)

Root Mean Squeare Propagation(RMSProp)

Adagrad의 단점인 Gradient 제곱합(𝑔 = 𝑔 + (𝑑𝐸)^2)을 지수평균으로 대체한 것이다.

Adaptive Moment Estimation(Adam)

RMSProp + Momentum 각각의 장점을 합친 알고리즘이다. Momentum과 같이 지금까지 계산한 기울기의 지수평균을 저장하고 RMSProp과 같이 기울기 제곱값의 지수평균을 저장한다.