시계열 데이터
- 순차적인 시간의 흐름에 따라 기록된 데이터를 의미
Y = T + S + C + R 또는 Y = T x S x C x R
| 추세(Trend) | 시간의 흐름에 따라 점진적이고 지속적인 변화 |
| 계절성(Seasonality) | 특정 주기에 따라 일정한 패턴을 갖는 변화 |
| 싸이클(Cycle) | 경제 또는 사회적 요인에 의한 변화이며, 일정 주기가 없고 장기적인 변화 |
| 잔차(Residuals) | 설명할 수 없는 변화 |
시계열 분석의 특징
- 현재 시점의 시계열 데이터를 분석하는 데 이전 시간의 값이 현재에도 영향을 끼칠 것이라는 가정하에 회귀분석을 진행
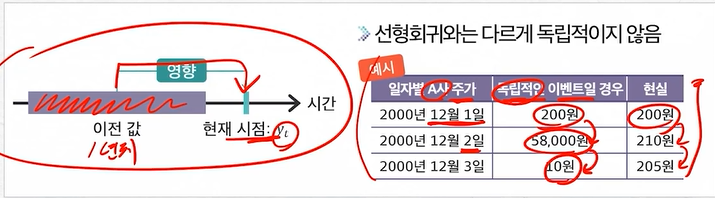
| 시계열 분석 | 단순 회귀 |
|---|---|
| 자기 상관(Autocorrelation) 존재 | 자기 상관 없음 |
| 대표적으로 자기회귀, 이동평균, 자기회귀누적이동평균, 벡터자기회귀 모델 등 존재 | 독립변수와 종속변수는 서로 다른 변수일 경우가 많음 |
| 현재 시점에 가까운 데이터일수록 서로 강한 관계를 맺는 경향 존재 | 선형 회귀로 시계열 데이터를 분석하려면 더 까다로운 가정 필요 > 선형성 가정이 필요 |
자귀회귀 모델(AR)
- AR모델은 시계열의 미래 값이 과거 값에 기반한다는 모델
- 즉, 이전 값의 영향을 받는 것이 특징

이동평균 모델(MA)
- 전체적인 편향성을 다루는 모델, 설명변수가 최근 오차항으로만 구성되어있는 것이 특징

ARIMA 모델
- AR과 MA를 동시에 고려하고, 누적(I)으로 추세까지 고려한 모델, '자기회귀 누적 이동평균 모델'

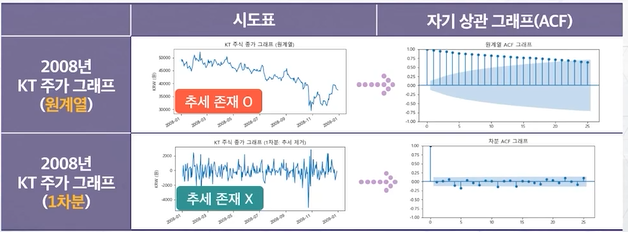
정상성
- 정상성을 나타내는 시계열은 관측치가 시간과 무관하여야 함
(즉 시간에 상관없이 일정한 평균과 분산을 가지고 있어야 함)
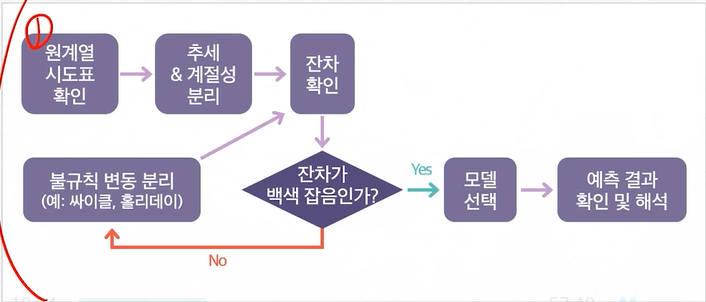
시계열 분석 순서
시계열 분석
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm
from statsmodels.tsa, stattools import adfuller #ADF는 정상성 검사를 위해 사용
from statsmodels.tsa.seasonal import seasonal_decompose #시계열 요소 분해
from statsmodels.tsa.arima.model import ARIMA # ARIMA 모델, SARIMA 모델
import pmdarima as pm #auto arima정상성 vs 비정상성
정상성 특징
- 정상 시계열은 평균이 일정
- 분산이 시점에 의존하지 않음
- 공분산은 시점에 의존하지 않음 (시차에는 의존)
- 정상성을 띄는 시계열은 장기적으로 예측 불가능한 시계열(e.g. 백색잡음 white noise)
비정상성
- 시간에 영향을 받는 시계열 (추세나 계절성)
비정상성 특징
- 시간의 흐름에 따라 시계열의 평균 수준이 다름
- // 추세를 가짐 (우상향, 우하향 추세 등)
- // 계절성이 있음
- // 시계열의 분산이 증가하거나 감소함
- 비정상성 시계열 ex) 여름에 아이스크림 판매량이 높고 겨울엔 낮다 (계절성)
정상 시계열 - 백색잡음 (white noise)
#정규분포에서 난수 365개 추출
np.random.seed(1)
x= np.random.randn(365)원계열 시도표 (Time Plot)
#백색잡음 시도표
plt.figure(figsize=(10,3))
plt.plot(np.arange(365), x)
plt.title('White Noise Time Series')
plt.xlabel('periods (t)')
plt.show()Augmented Dickey Fuller Test 단위근 검정 (ADF test)
Augmented Dickey Fuller Test 가설검정
H0 : 정상성이 있는 시계열이 아님
H1 : 정상성이 있는 시계열
귀무가설을 기각해야 정상성이 있는 시계열result = adfuller(x)
result
결과 귀무가설 기각 -> 정상 시계열ACF와 PACF
fig.axes = plt.subplots(1, 2, figsize=(15,4))
fig = sm.graphics.tsa.plot_acf(x, lags=40, ax=axes[0])
fig = sm.graphics.tsa.plot_pacf(x, lags=40, ax=axes[1])
fig.suptitle('~', y = 1.05)
plt.show()
자기상관 및 편자기상관 없음 -> 정상성비정상성 시계열 (추세존재)
#추세 생성 및 백색잡음에 추세 추가
trend = mp.linspace(1, 15, 365) #추세 생성
x_v_trend = x + trend #백색잡음 x에 추세 추가원계열 시도표(Time plot)
#추세 존재 시계열의 시도표
plt.figure(figsize=(10,3))
plt.plot(np.arange(365), x_v_trend)
plt.title~
plt.xlabel~
plt.show()검정 진행 -
ARIMA -- AR(5)
# statsmodels가 제공하는 ARIMA 사용
ar_mod = ARIMA(x_v_trend, order=(5, 0, 0) #AR order만 5 따라서 AR(5) 모델링
result - ar_mod.fit()
#실 데이터 vs 모델 결과
plt.figure(figsize=(10, 3))
plt.plot(np.arange(365), x_v_trend)
plt.plot(np.arange(365), result.fittedvalues)
plt.show()
print(result.summary())
result.plot_diagnostics(figsize=(16, 8)) #표들..
plt.show()ARIMA -- I(1)
#차분만 이용한 추세 제거 모델링
arima_mod2 = ARIMA(x_v_trend, order=(0, 1, 0)
result = arima_mod2.fit()
plt.figure(figsize=(15, 5))
plt.plot(np.arange(365), x_v_trend)
plt.plot(np.arange(365), result.fittedvalues)
plt.show()
print(result.summary())시계열 성분 분해(Time Series Decomposition)
#data 불러오기
df = pd.read_csv('./data/latte_ice_cream.csv')
#시계열 데이터로 변환
df['time'] = pd.to_datetime(df['year'].astype(str) + '-' + df['month'].astype(str) + '-' + df['date'].astype(str))
df= df.set_index('time', drop=True)
#time series 생성
ts = df['sales_amount']
ts시도표(Time Plot)
ts.plot(figsize=(10,3))
plt.show()
1. 추세
2. 계절성
3. 분산계절성 분해(seasonal decompose)
# statsmodels제공
decomp = seasonal_decompose(ts, model='additive', period=12)
#시계열 분해 그래프
fig = decomp.plot()
fig.set_size_inches((12,8))
#multiplicative 분해 방식
decomp = seasonal_decompose(ts, model='multiplicative', period=12)SARIMAAX : ARIMA + 계절성(S)
#seasonality를 ARIMA모델링
s_mod = sm.tsa.statespace.SARIMAX(ts, order=(1, 1, 0), seasonal_order=(1, 1, 0, 12))
result = s_mod.fit()
print(result.summary())
#예측그래프도 그려줌
.
.
.
